Київська державна академія водного транспорту
Кафедра математики
Модульна контрольна робота №1 з дисципліни
«Теорія ймовірностей та математична статистика»
Спеціальність: Менеджмент організацій
Курс: 2
Семестр:2
Форма навчання: денна
ВАРІАНТ 5
Скільки п’ятизначних парних чисел можна скласти з цифр 0, 1, 2, 3, 5, 7 за умови, що в числі цифри не повторюються?
В ящику 15 білих і 10 чорних кульок. Навмання виймають дві кульки. Знайти ймовірність того, що серед них: а) обидві кульки білі; б) обидві кульки чорні; в) обидві кульки однакового кольору; г) дістали кульки різних кольорів; д) хоча б одна кулька біла.
Три елементи обчислювального пристрою працюють незалежно. Ймовірність безвідмовної роботи кожного елемента за час t дорівнює 0,8. Визначити ймовірність того, що протягом часу t : а) всі елементи вийдуть з ладу; б) тільки один елемент працюватиме безвідмовно; г) два елементи не відмовлять; г) всі три елементи працюватимуть справно.
Дві секретарки заповнюють документи, які складають у спільну папку. Ймовірність того, що помилки в документі зробить перша секретарка, становить 0,05, а друга – 0,1. Перша секретарка заповнила 20 документів, а друга – 30. Навмання взятий з папки документ містить помилки. Визначити ймовірність того, що його заповнювала перша секретарка.
В ящику 5 білих, 3 чорних та 2 синіх кульки. Навмання виймають 2 кульки. {число білих кульок серед вилучених}. Скласти закон розподілу дискретної випадкової величини . Обчислити математичне сподівання, дисперсію та середнє квадратичне відхилення .
Відомо, що випадкова величина може набувати тільки два значення : та , причому . Скласти закон розподілу випадкової величини , якщо відомо значення ймовірності можливого значення , значення математичного сподівання та дисперсії :
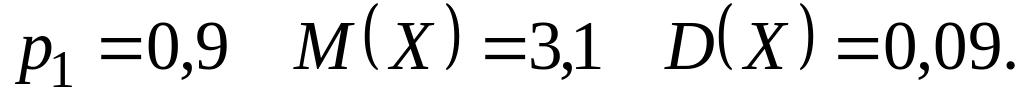
Затверджено на засіданні кафедри математики КДАВТ.
Протокол № від « » 2010р.
Екзаменатор ___________________ в.о. доцента Кліндухова В.М.,
кандидат пед. наук
Зав. кафедрою ___________________ доцент Ляшко О.В.,
кандидат фіз.-мат. наук
Київська державна академія водного транспорту
Кафедра математики
Модульна контрольна робота №1 з дисципліни
«Теорія ймовірностей та математична статистика»
Спеціальність: Менеджмент організацій
Курс: 2
Семестр:2
Форма навчання: денна
ВАРІАНТ 6
Шифр складається з п’яти елементів, де перші три – різні цифри, а дві останні – різні букви латинського алфавіту. Визначити кількість можливих варіантів кодів.
В ящику 15 білих і 10 чорних кульок. Навмання виймають дві кульки. Знайти ймовірність того, що серед них: а) обидві кульки білі; б) обидві кульки чорні; в) обидві кульки однакового кольору; г) дістали кульки різних кольорів; д) хоча б одна кулька біла.
Ймовірність того, що відвідувач взуттєвого магазину зробить покупку, становить 0,2. Визначити ймовірність того, що: а) один із п’яти відвідувачів придбає взуття; б) жоден з п’яти відвідувачів не зробить покупки; в) хоча б один з п’яти відвідувачів придбає взуття?
В ящик, який містить 7 білих і 4 чорні кульки, з однаковою ймовірністю опущена біла або чорна кулька. Після цього з ящика навмання виймають кульку. Знайти ймовірність того, що вона біла.
В ящику 5 білих, 3 чорних та 2 синіх кульки. Навмання виймають 2 кульки. {число чорних кульок серед вилучених}. Скласти закон розподілу дискретної випадкової величини . Обчислити математичне сподівання, дисперсію та середнє квадратичне відхилення .
Відомо, що випадкова величина може набувати тільки два значення : та , причому . Скласти закон розподілу випадкової величини , якщо відомо значення ймовірності можливого значення , значення математичного сподівання та дисперсії :
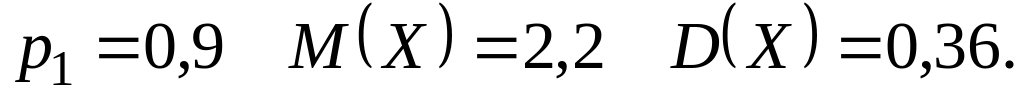
Затверджено на засіданні кафедри математики КДАВТ.
Протокол № від « » 2010р.
Екзаменатор ___________________ в.о. доцента Кліндухова В.М.,
кандидат пед. наук
Зав. кафедрою ___________________ доцент Ляшко О.В.,
кандидат фіз.-мат. наук