МІНІСТЕРСТВО НАУКИ ТА ОСВІТИ УКРАЇНИ
КИЇВСЬКА ДЕРЖАВНА АКАДЕМІЯ ВОДНОГО ТРАНСПОРТУ
імені гетьмана Петра Конашевича-Сагайдачного
ФАКУЛЬТЕТ ЕКОНОМІКИ ТРАНСПОРТУ
Завдання модульної контрольної роботи №1 з курсу
Теорія ймовіностей та математична статистика
для студентів другого курсу напряму
«Менеджмент організацій»
денної форми навчання
Укладач – в.о. доцента
кафедри математики КДАВТ
Кліндухова В.М.
Затверджено
на засіданні кафедри математики КДАВТ
протокол № від 2010 року
Київ-2010
КИЇВСЬКА ДЕРЖАВНА АКАДЕМІЯ ВОДНОГО ТРАНСПОРТУ
Кафедра математики
Модульна контрольна робота №1 з дисципліни
«Теорія ймовірностей та математична статистика»
Спеціальність: Менеджмент організацій
Курс: 2
Семестр:2
Форма навчання: денна
ВАРІАНТ 1
Скільки парних п’ятизначних чисел можна утворити з цифр 0, 1, 2, 3, 4 так, щоб усі цифри числа були різними?
В ящику 15 білих і 10 чорних кульок. Навмання виймають дві кульки. Знайти ймовірність того, що серед них: а) обидві кульки білі; б) обидві кульки чорні; в) обидві кульки однакового кольору; г) дістали кульки різних кольорів; д) хоча б одна кулька біла.
По каналу зв’язку передається повідомлення з десяти знаків. Ймовірність помилки при передачі одного знаку дорівнює 0,1. Знайти ймовірність того, що повідомлення: а) не містить помилок; б) містить рівно три помилки; в) містить не більше трьох помилок.
Пасажир для придбання квитка може навмання звернутися до однієї з чотирьох кас. Ймовірності наявності квитка в касах відповідно рівні 0,6; 0,3; 0,8; 0,5. Пасажир звернувся до однієї з кас і купив квиток. Яка ймовірність того, що квиток він придбав у першій касі?
Скласти закон розподілу дискретної випадкової величини
,
де
{число
випадань “герба” в п’яти незалежних
киданнях монети}. Обчислити
математичне сподівання, дисперсію та
середнє квадратичне відхилення
.
Відомо, що випадкова величина
може набувати тільки два значення :
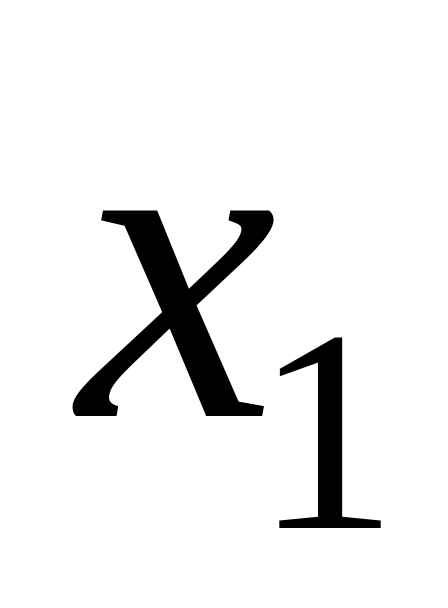та
,
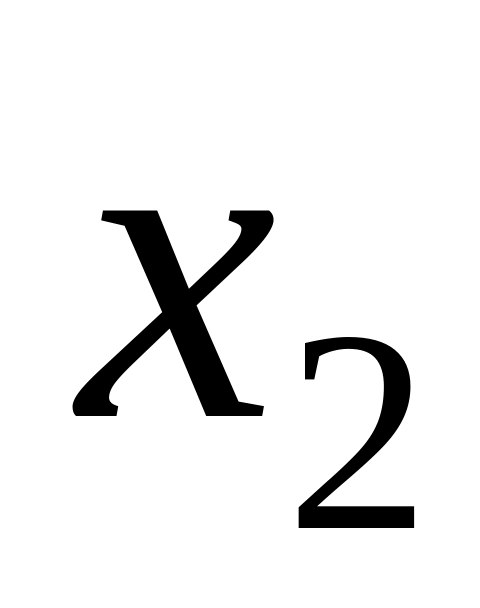причому
.
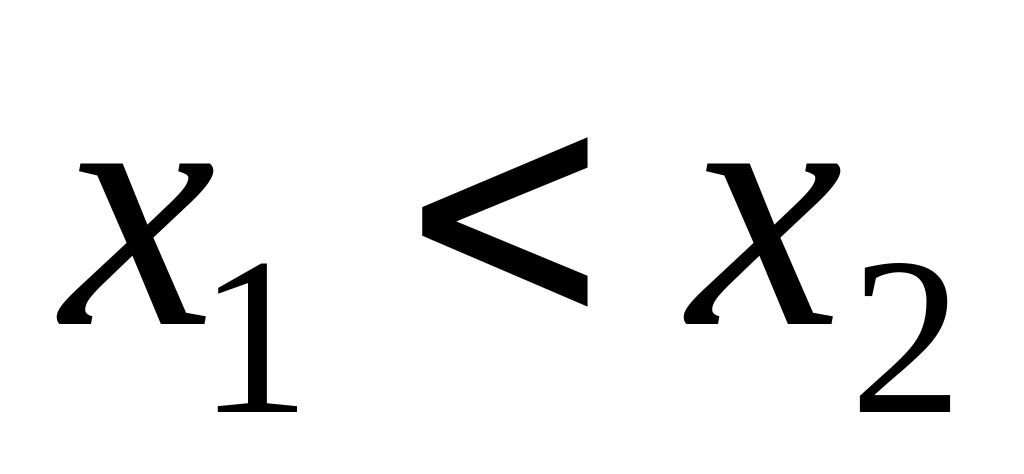Скласти закон розподілу випадкової
величини
,
якщо відомо значення ймовірності
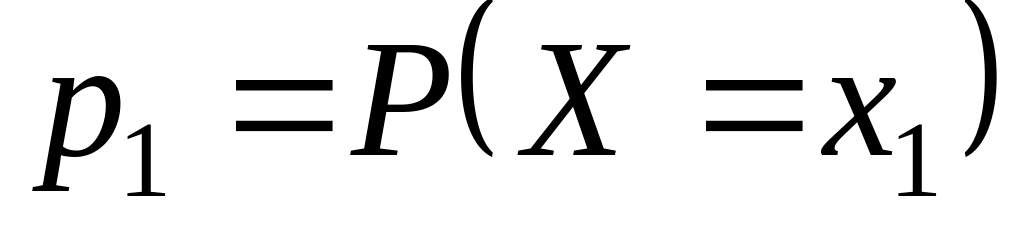можливого значення
,
значення математичного сподівання
та дисперсії
:
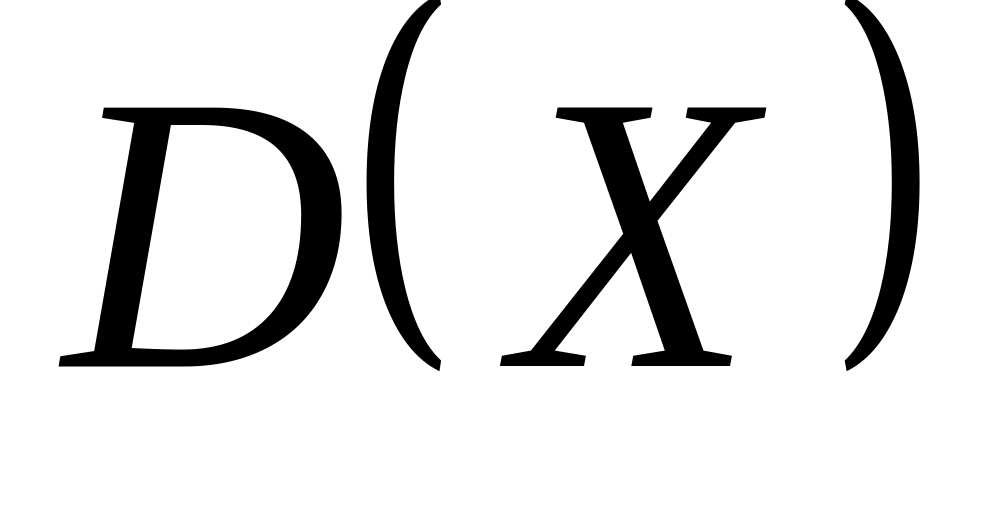Затверджено на засіданні кафедри математики КДАВТ.
Протокол № від « » 2010р.
Екзаменатор ___________________ в.о. доцента Кліндухова В.М.,
кандидат пед. наук
Зав. кафедрою ___________________ доцент Ляшко О.В.,
кандидат фіз.-мат. наук
Київська державна академія водного транспорту
Кафедра математики
Модульна контрольна робота №1 з дисципліни
«Теорія ймовірностей та математична статистика»
Спеціальність: Менеджмент організацій
Курс: 2
Семестр:2
Форма навчання: денна
ВАРІАНТ 2
Студенти одного з курсів вивчають 8 навчальних дисциплін. Скількома способами можна розклад занять на понеділок, якщо в цей день треба запланувати три лекції з різних предметів?
В ящику 15 білих і 10 чорних кульок. Навмання виймають дві кульки. Знайти ймовірність того, що серед них: а) обидві кульки білі; б) обидві кульки чорні; в) обидві кульки однакового кольору; г) дістали кульки різних кольорів; д) хоча б одна кулька біла.
Ймовірність виграшу по одному лотерейному білету дорівнює 0,05. Яка ймовірність, маючи 5 білетів, виграти: а) по всім білетам; б) не виграти по жодному з білетів; в) виграти хоча б по одному з білетів?
До групи спортсменів входить 20 бігунів, 6 велосипедистів та 4 гімнасти. Ймовірність виконання норми розряду для бігуна становить 0,95, для велосипедиста – 0,8, для гімнаста – 0,75. Визначити ймовірність того, що вибраний навмання спортсмен виконає норму розряду.
Скласти закон розподілу дискретної випадкової величини , де {число випадань “цифри” в п’яти незалежних киданнях монети}. Обчислити математичне сподівання, дисперсію та середнє квадратичне відхилення .
Відомо, що випадкова величина може набувати тільки два значення : та , причому . Скласти закон розподілу випадкової величини , якщо відомо значення ймовірності можливого значення , значення математичного сподівання та дисперсії :
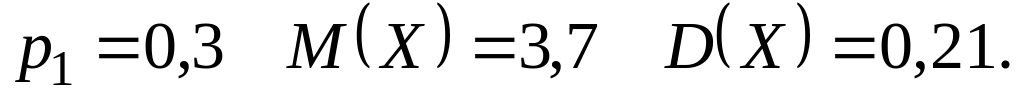
Затверджено на засіданні кафедри математики КДАВТ.
Протокол № від « » 2010р.
Екзаменатор ___________________ в.о. доцента Кліндухова В.М.,
кандидат пед. наук
Зав. кафедрою ___________________ доцент Ляшко О.В.,
кандидат фіз.-мат. наук