Лекция 3: Системы. Модели систем

Центральной концепцией теории систем, кибернетики, системного подхода, всей системологии является понятие «системы». Поэтому очень многие авторы анализировали это понятие, развивали определение системы до различной степени формализации.

Первое определение системы

Начнем с рассмотрения искусственных, т.е. создаваемых человеком систем. Как уже отмечалось, любая деятельность человека носит целенаправленный характер. Наиболее четко это прослеживается на примере трудовой деятельности. Цели, которые ставит перед собой человек, редко достижимы только за счет его собственных возможностей или внешних средств, имеющихся у него в данный момент. Такое стечение обстоятельств называется «проблемной ситуацией». Проблемность существующего положения осознается в несколько «стадий»: от смутного ощущения что «что-то не так», к осознанию потребности, затем к выявлению проблемы и, наконец, к формулировке цели.

Цель — это субъективный образ (абстрактная модель) несуществующего, но желаемого состояния среды, которое решило бы возникшую проблему. Вся последующая деятельность, способствующая решению этой проблемы, направлена на достижение поставленной цели, т.е. как работа по созданию системы. Другими словами: система есть средство достижения цели.

Приведем несколько упрощенных примеров систем, предназначенных для реализации определенных целей.

N	Цель	Система
1	В произвольный момент указать время	Часы
2	Обеспечить выпечку хлеба в заданном ассортименте для большого количества людей	Пекарня
3	Передать зрительную и звуковую информацию на большое расстояние практически мгновенно	Телевидение
4	Обеспечить перемещение людей в городе	Городской транспорт

Отметим, что далеко не просто сформулировать цели так, чтобы имелось действительно очевидное соответствие между целями и системами. Например, только слова «практически мгновенно» в примере 3 отличает цель телевидения от цели кино или пересылки видеокассет. В то же время, между целью (абстрактной и конечной моделью) и реальной системой нет, и не может быть однозначного соответствия: для достижения заданной цели могут быть избраны разные средства — системы. С другой стороны, заданную реальную систему можно использовать и для других целей, прямо не предусмотренных при ее создании.

Момент формулирования цели — один из важнейших этапов создания систем. Обычно цели уточняются итеративно, с многократными изменениями и дополнениями.

Модель «черного ящика»

Перейдем от первого определения системы к его визуальному эквиваленту. Во-первых, приведенное определение ничего не говорит о внутреннем устройстве системы. Поэтому ее можно изобразить в виде непрозрачного «ящика», выделенного из окружающей среды. Подчеркнем, что уже эта, максимально простая, модель по-своему отражает два следующих важных свойства системы: целостность и обособленность от среды.

Во-вторых, в определении системы косвенно говорится о том, что хотя «ящик» и обособлен, выделен из среды, но не является полностью от нее изолированным.

Рис.3.1 — Модель «черного ящика»

Иначе говоря, система связана со средой и с помощью этих связей воздействует на среду. Эти связи называются выходами системы. Подчеркнем еще раз, что выходы системы в данной графической модели соответствуют слову «цель» в словесной модели системы (в первом определении). Кроме того, система является средством, поэтому должны существовать и воздействия на нее, т.е. такие связи со средой, которые направлены извне в систему, которые называются входами системы.

В результате мы построили модель системы, которая получила название «черного ящика» (см. рис.3.1). Это название образно подчеркивает полное отсутствие сведений о внутреннем содержании системы. В модели задаются только входные и выходные связи системы со средой, т.е. множество X и Y входных и выходных переменных. Такая модель, несмотря на внешнюю простоту и на отсутствие сведений о внутреннем строении системы, часто оказывается очень полезной. Отметим, однако, что построение модели «черного ящика» не является тривиальной задачей, так как на вопрос о том, сколько и какие именно входы и выходы следует включать в модель, ответ не прост и не всегда однозначен.

Модель состава системы

При рассмотрении любой системы обнаруживается, что ее целостность и обособленность, отображенные в модели черного ящика, выступают как внешние свойства. Внутренность же «ящика» оказывается неоднородной, что позволяет различать составные части самой системы. При более детальном рассмотрении некоторые части системы могут быть, в свою очередь, разбиты на составные части и т.д. Те части системы, которые мы рассматриваем как неделимые, называются элементами. Части системы, состоящие более чем из одного элемента, называют подсистемами. При необходимости можно ввести обозначения или термины, указывающие на иерархию частей. В результате получается модель состава системы, описывающая из каких подсистем и элементов она состоит (см. рис.3.2).

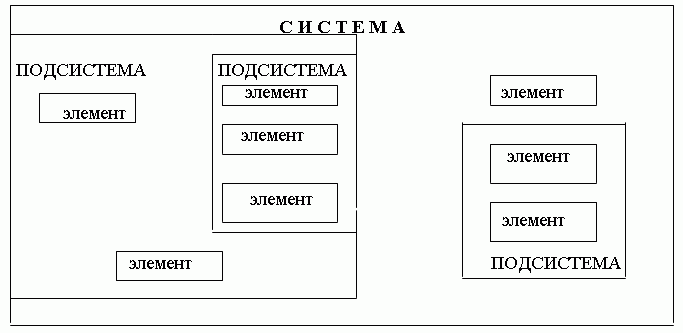
Рис.3.2.(a) — Модель состава системы

Пример модели состава системы:

Система	Подсистема	Элементы
Система телевидения «Орбита»	Подсистема передачи	Центральная телестудия
		Антенно-передающий центр
	Канал связи	Среда распространения радиоволн
		Спутники ретрансляторы
	Приемная подсистема	Местные телецентры
		Телевизоры потребителей

Рис. 3.2.(b) — Модель состава системы

Модель структуры системы

Несмотря на полезность рассмотренных выше моделей систем, существуют проблемы, решить которые с помощью таких моделей нельзя. Например, чтобы получить велосипед, недостаточно иметь отдельные его детали (хотя состав системы налицо). Необходимо еще правильно соединить все детали между собой, или, говоря общо, установить между элементами определенные связи — отношения.

Совокупность необходимых и достаточных для достижения цели отношений между элементами называется структурой системы.

Когда мы рассматриваем некую совокупность объектов как систему, то из всех отношений мы выбираем важные, т.е. существенные для достижения цели. Точнее, в модель структуры (в список отношений) мы включаем только конечное число связей, которые существенны по отношению к рассматриваемой цели. Например, при расчете механизмов не учитываются силы взаимного притяжения его деталей, хотя, согласно закону всемирного тяготения, такие силы объективно существуют. Зато вес деталей учитывается обязательно.

Второе определение системы. Структурная схема системы

Объединяя все изложенное в предыдущих параграфах, можно сформулировать второе определение системы: система есть совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как целое.

Очевидно, что представленные определения охватывают модели «черного ящика», состава и структуры. Все вместе они образуют еще одну модель, которую будем называть структурной схемой системы. В структурной схеме указываются все элементы системы, все связи между элементами внутри системы и связи определенных элементов с окружающей средой (входы и выходы системы).

Рассмотрим систему «синхронизируемые часы». Считаем, что в состав такой системы входят три элемента: датчик, индикатор и эталон времени. Структура часов определяется следующими отношениями между парами элементов:

Пара элементов	Связь между ними
Датчик и индикатор	Однозначное соответствие
Эталон и датчик	Приблизительное соответствие
Индикатор и эталон	Периодическое сравнение и устранение расхождения

Описанные связи указаны стрелками 1-3 между элементами на рис.3.3. Вход 4 изображает поступление энергии извне, вход 5 соответствует регулировки индикатора, вход 6 — показанию часов.

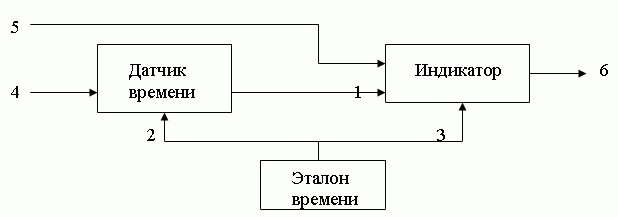
Рис.3.3 — Структурная схема системы синхронизируемые часы

Все структурные схемы имеют нечто общее и это побудило математиков рассматривать их как объект математических исследований. Для этого пришлось абстрагироваться от содержательной стороны структурных схем. В результате получилась схема, в которой обозначается только наличие элементов и связей между ними. Такая схема называется графом.

Граф состоит из обозначений элементов произвольной природы, называемых вершинами, и обозначений связей между ними, называемых ребрами (либо дугами). На рис.3.4 изображен граф: вершины обозначены в виде кружков, ребра в виде линий.

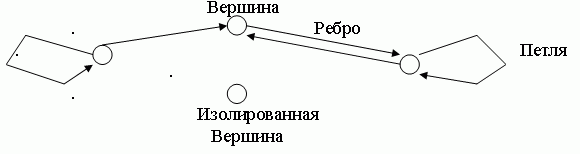
Рис.3.4 — Пример графа

Если направления связей не обозначаются, то граф называется неориентированным, при наличии стрелок — ориентированным. Данная пара вершин может быть соединена любым количеством ребер; вершина может быть соединена сама с собой (тогда ребро называется петлей). Если в графе требуется отразить другие различия между элементами или связями, то либо приписывают ребрам различные веса (взвешенные графы), либо раскрашивают вершины или ребра (раскрашенные графы).

Для графов построена интересная и содержательная теория, имеющая многочисленные приложения. Разнообразные задачи этой теории связаны с различными преобразованиями графов, а также с возможностью рассмотрения различных отношений на графах: весов, рангов, цветов, вероятностных характеристик (стохастические графы) и т.д. Поскольку множества вершин и ребер формально можно поменять местами, получается два разных представления системы в виде вершинного или реберного графа.

Графы могут изображать любые структуры, если не накладывать ограничений на пересекаемость ребер. Некоторые типы структур имеют особенности, важные для практики, они выделены из других и получили специальные названия. Так, в организационных системах часто встречаются (см.рис.3.5) линейные, древовидные (иерархические) и матричные структуры; в технических системах чаще встречаются сетевые структуры; особое место в теории систем занимают структуры с обратными связями, которые соответствуют кольцевым путям в ориентированных графах.

Структурная схема системы является наиболее подробной и полной моделью любой системы на данном этапе нашего познания. При этом всегда остается актуальным вопрос об адекватности этой модели, разрешаемый только на практике.

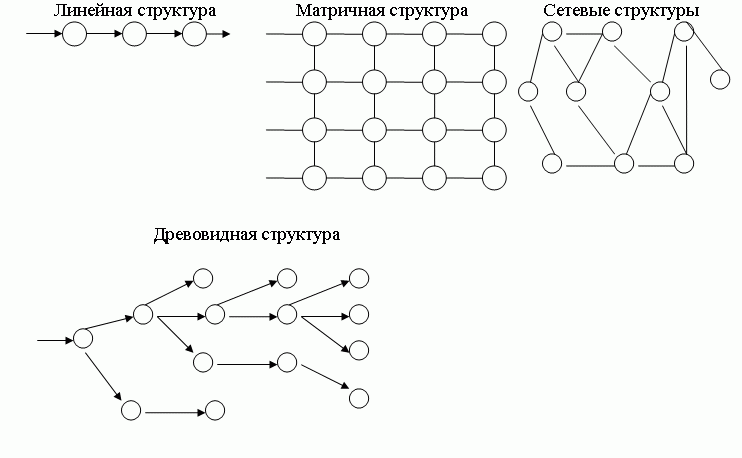
Рис. 3.5 — Линейные, древовидные, матричные и сетевые структуры

Динамические модели систем

До сих пор основное внимание было уделено понятию системы, ее составу и устройству. Были рассмотрены модели, которые являются как бы «фотографиями» системы, отображают ее в некоторый момент времени. В этом смысле рассмотренные варианты моделей могут быть названы статическими моделями. Следующий шаг в исследовании систем состоит в том, чтобы понять и описать, как система «работает», что происходит с ней самой и окружающей средой в ходе реализации поставленной цели.

Системы, в которых происходят какие бы то ни было изменения со временем называются динамическими, а модели, отображающие эти изменения, — динамическими моделями систем.

Для разных объектов и систем разработано большое количество динамических моделей, описывающих процессы с различной степенью детализации. Однако всегда развитие моделей происходит в той же последовательности, как это было изложено выше: от «черного ящика» к «белому».

Функционирование и развитие

Уже на этапе «черного ящика» различают два типа динамики системы: функционирование и развитие. Под функционированием подразумевают процессы, которые происходят в системе, стабильно реализующей фиксированную цель. Функционируют, например, часы, городской транспорт, радиоприемник и т.д.

Развитием» называют то, что происходит с системой при изменении ее целей. Характерной чертой развития является тот факт, что существующая структура перестает соответствовать новой цели. Для обеспечения новой функции приходится изменять структуру, а иногда и состав системы, т.е. перестраивать всю систему. Возможны и такие системы, для функционирования которых какие-то ее подсистемы должны быть постоянно в развитии. Типы динамических моделей.

При математическом моделировании некоторого процесса его конкретная реализация описывается в виде соответствия между элементами множества входов системы X «возможных значений» x и элементов упорядоченного множества T «моментов времени» t, т.е. в виде отображения:

T → X: x(t) ∈ X^T, t ∈ T.

С помощью этих понятий строятся математические модели систем.

Рассматривая выход y(t) системы как ее реакцию на входы x(t)= u(t),v(t) (управляемые u(t) и управляемые v(t)), можно представить модель «черного ящика» как совокупность двух процессов (см. рис.3.6):

X^T = {x(t)} и Y^T = {y(t)}, t ∈ T

Рис.3.6 — Динамическая модель «черного ящика»: задание процесса на входах и выходах системы

Если даже считать y(t) результатом некоторого преобразования Ф процесса x(t), т.е. y(t)=Ф[x(t)], то модель «черного ящика» предполагает, что это преобразование неизвестно. В том случае, когда имеем модель «белого ящика» соотношение между входом и выходом должно быть описано. Способ описания зависит от того, что нам известно и в какой форме можно использовать эти знания. На практике наблюдая входы и выходы системы можно восстановить функцию y=Ф(x). По существу это задача о переходе от модели «черного ящика» к модели «белого ящика» по наблюдениям входов и выходов при условии безинерционности системы.

Общая математическая модель динамики

Класс систем, которые можно считать безинерционными, весьма узок. Необходимо строить математические модели систем, выход которых определяется не только значением входа в данный момент времени, но и теми значениями, которые были на входе в предыдущие моменты. В наиболее общей модели это достигается введением понятия состояния системы как некоторой внутренней характеристики, значение которой в настоящий момент времени определяет текущее значение выходной величины. Обозначим это состояние через z(t). Сказанное выше означает существование такого отображения

η: Z × T → Y, что y(t) = η[t, z(t)]

Явная зависимость от t введена для учета возможности изменения зависимости выхода от состояния с течением времени. Это отображение называется отображением выхода.

Для завершения построения модели нужно описать связь между входом и состоянием, т.е. ввести параметрическое семейство отображений

μ_α: Z × X() → Z,

заданных для всех значений параметров

t ∈ T, τ ∈T и τ ≤ t

Это означает принятие аксиомы о том, что состояние в любой момент t однозначно определяется состоянием z и отрезком реализации входа х( )

z(t) = μ_α[Z_τ, X()] = σ[t, τ, Z_τ, X()].

Такое отображение называется переходным отображением.

Итак, математическая модель системы, соответствующая уровню «белого ящика», — это задание множества входов, состояний и выходов, и связей между ними:

X →^σ Z →^η Y

Конкретизируя множества X, Z и Y и отображения можно перейти к содержательным моделям различных систем. Говорят о дискретных или непрерывных по времени системах в зависимости от того, дискретно или непрерывно множество Т. Далее, если множества X, Z и Y дискретной по времени системы имеет конечное число элементов, то такую систему называют конечным автоматом. Это довольно простой класс систем в том смысле, что для исследования конечных автоматов необходимы лишь методы логики и алгебры. В то же время это широкий и практически важный класс, так как в него входят все дискретные (цифровые) измерительные, управляющие и вычислительные устройства.

Если X, Z и Y — линейные пространства, а есть- линейные операторы, то и система называется линейной. Если к линейной системе предъявить дополнительные требования, состоящие в том, чтобы пространства имели топологическую структуру, а отображения были непрерывны в этой топологии, то мы приходим к гладким системам. Не вдаваясь в математические подробности, отметим, что задание топологической структуры множества позволяет строго определить основные понятия анализа на этом множестве, например сходимость последовательностей на нем, а так же вводить метрику (меру близости между элементами пространства).

Стационарные системы

Большой интерес на практике представляют стационарные системы, т.е. системы, свойства которых не изменяются со временем. Стационарность означает независимость от времени t и инвариантность функции к сдвигу во времени:

h[t, z(t)] = h[z(t)],

σ[t, t₀, z, x(.)] = σ[t+τ₀, t₀+τ, z,x_τ(.)].

Конкретизация моделей динамических систем на этом, конечно, не заканчивается. Приведенные модели скорее всего являются просто примерами, которые можно рассматривать отдельно. Но на одном свойстве реальных динамических систем следует остановиться. Речь идет о подчинении реальных систем принципу причинности. Согласно этому принципу, отклик системы на некоторое воздействие не может начаться раньше самого воздействия. Это условие, очевидное для реальных систем, совсем не автоматически выполняется в рамках их математических моделей. При этом модель, в которой нарушается принцип причинности, совсем не является «плохой», бесполезной. Примером служит модель фильтра с конечной полосой пропускания. Отклик такой системы на короткий импульс имеет вид Sin(wt)/(wt), т.е. начинается в минус бесконечности. Несмотря на явное нарушение принципа причинности, такую модель широко используют в радиотехнике. Однако, как только возникает вопрос о практической реализации такого фильтра, используются различные допущения. В связи с этим одна из проблем теории динамических систем состоит в выяснении условий физической реализуемости теоретических моделей, т.е. конкретных ограничений, которые приходится накладывать на модель при соблюдении принципа причинности.

Подведем итог

Оказывается, что при всем многообразии реальных систем принципиально различных типов моделей систем очень не много: модель типа «черный ящик», модель состава, модель структуры, а также их разумные сочетания и прежде всего объединения всех трех типов моделей, т.е. структурная схема системы. Это относится как к статическим моделям, отображающим фиксированное состояние системы, так и к динамическим моделям, отображающим характер временных процессов, которые происходят с системой.

Все указанные типы моделей являются формальными, относящимися к любым системам и, следовательно, не относящимися ни к одной конкретной системе. Чтобы получить модель заданной системы, нужно придать формальной модели конкретное содержание, т.е. решить, какие аспекты реальной системы включать как элементы модели, а какие — нет. Этот процесс обычно неформализуем, поскольку признаки существенности не удается формализовать. Столь же слабо формализованными являются признаки элементарности и разграничения между подсистемами.

В силу сказанного, процесс построения содержательных моделей является процессом интеллектуальным, творческим. Тем не менее эксперту, разрабатывающему содержательную модель, помогают формальная модель и рекомендации по ее наполнению конкретным содержанием.

Общие сведения о методологии IDEF0

Создание современных информационных систем представляет собой сложнейшую задачу, решение которой требует применения специальных методик и инструментов. Неудивительно, что в последнее время среди системных аналитиков и разработчиков значительно вырос интерес к CASE-технологиям и инструментальным CASE-средствам, позволяющим максимально систематизировать и автоматизировать все этапы разработки программного обеспечения: СASE-средство верхнего уровня Bpwin, поддерживающее методологии IDEFO. Erwin — case средство, позволяющее осуществить прямое и обратное проектирование базы данных, поддерживает методологию IDEF1X. Сase-средство BPwin значительно облегчают задачу создания информационной системы, позволяя осуществить декомпозицию сложной системы на более простые с тем, чтобы каждая из них могла проектироваться независимо, и для понимания любого уровня проектирования достаточно было оперировать с информацией о немногих ее частях.

Стандарт IDEF0 предназначен для функционального моделирования. Его применение — это сравнительно новое направление, но уже достаточно популярное и заслужившее серьезное отношение к себе. В основе стандарта лежит понятие функции, под которой понимается управляемое действие над входными данными, осуществляющееся посредством определенного механизма, результатом его являются выходные данные.

Стандарт IDEF0 базируется на трех основных принципах:

1. Принцип функциональной декомпозиции — любая функция может быть разбита на более простые функции;

2. Принцип ограничения сложности — количество блоков от 2 до 8 (в BPwin) условие удобочитаемости;

3. Принцип контекста — моделирование делового процесса начинается с построения контекстной диаграммы, на которой отображается только один блок — главная функция моделирующей системы.

Специализированным средством создания IDEF0 диаграмм является BPwin. Это лучшее средство в своем классе. Пакет BPWin предназначен для функционального моделирования и анализа деятельности предприятия. Модель в BPWin представляет собой совокупность SADT-диаграмм, каждая из которых описывает отдельный процесс в виде разбиения его на шаги и подпроцессы. С помощью соединяющих дуг описываются объекты, данные и ресурсы, необходимые для выполнения функций. Имеется возможность для любого процесса указать стоимость, время и частоту его выполнения. Эти характеристики в дальнейшем могут быть просуммированы с целью вычисления общей стоимости затрат — таким образом выявляются узкие места технологических цепочек, определяются затратные центры. BPWin может импортировать фрагменты информационной модели из ERWin (при этом сущности и атрибуты информационной модели ставятся в соответствие дугам SADT-диаграммы). Генерация отчетов по модели может осуществляться в формате MS Word и MS Excel.

Результатом применения методологии SADT является модель, которая состоит из диаграмм, фрагментов текстов и глоссария, имеющих ссылки друг на друга. Диаграммы — главные компоненты модели, все функции и интерфейсы на них представлены как блоки и дуги. Место соединения дуги с блоком определяет тип интерфейса. Диаграммы строятся при помощи блоков (см. рис.1.1).Каждый блок описывает какое-либо законченное действие. Четыре стороны блока имеют различное предназначение. Слева отображаются входные данные — исходные ресурсы для описываемой блоком функции (исходная информация, материалы); Справа показываются выходные ресурсы — результирующие ресурсы, полученные в результате выполнения описываемой блоком функции; Сверху управление — то, что воздействует на процесс выполнения описываемой блоком функции и позволяет влиять на результат выполнения действия (средства управления, люди); Механизм изображается снизу — это то, посредством чего осуществляется данное действие (станки, приборы, люди и т.д.).

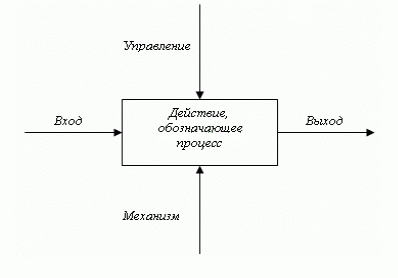
Рис.3.7 — Построение диаграммы Bpwin

Иерархия диаграмм

Построение SADT-модели начинается с представления всей системы в виде простейшей компоненты — одного блока и дуг, изображающих интерфейсы с функциями вне системы. Поскольку единственный блок представляет всю систему как единое целое, имя, указанное в блоке, является общим. Это верно и для интерфейсных дуг — они также представляют полный набор внешних интерфейсов системы в целом. Затем блок, который представляет систему в качестве единого модуля, детализируется на другой диаграмме с помощью нескольких блоков, соединенных интерфейсными дугами. Эти блоки представляют основные подфункции исходной функции. Данная декомпозиция выявляет полный набор подфункций, каждая из которых представлена как блок, границы которого определены интерфейсными дугами. Каждая из этих подфункций может быть декомпозирована подобным образом для более детального представления.

Во всех случаях каждая подфункция может содержать только те элементы, которые входят в исходную функцию. Кроме того, модель не может опустить какие-либо элементы, т.е., как уже отмечалось, родительский блок и его интерфейсы обеспечивают контекст. К нему нельзя ничего добавить, и из него не может быть ничего удалено.

Модель SADT представляет собой серию диаграмм с сопроводительной документацией, разбивающих сложный объект на составные части, которые представлены в виде блоков. Детали каждого из основных блоков показаны в виде блоков на других диаграммах. Каждая детальная диаграмма является декомпозицией блока из более общей диаграммы. На каждом шаге декомпозиции более общая диаграмма называется родительской для более детальной диаграммы.

Дуги, входящие в блок и выходящие из него на диаграмме верхнего уровня, являются точно теми же самыми, что и дуги, входящие в диаграмму нижнего уровня и выходящие из нее, потому что блок и диаграмма представляют одну и ту же часть системы. Каждый блок на диаграмме имеет свой номер. Блок любой диаграммы может быть далее описан диаграммой нижнего уровня, которая, в свою очередь, может быть далее детализирована с помощью необходимого числа диаграмм. Таким образом, формируется иерархия диаграмм.

Для того, чтобы указать положение любой диаграммы или блока в иерархии, используются номера диаграмм. Например, А21 является диаграммой, которая детализирует блок 1 на диаграмме А2. Аналогично, А2 детализирует блок 2 на диаграмме А0, которая является самой верхней диаграммой модели.

Как уже отметили главный процесс — это создать курсовой проект. На входе этого процесса — исходные данные по заданию. В качестве управляющего воздействия выступает методическое пособие, ГОСТы, необходимые требования.

Механизм осуществления создания курсового проекта — программное обеспечение, с помощью которого представлен материал и разработан проект и исполнитель проекта(студент)

Рис.3.8 — Блок «Создать курсовой проект»

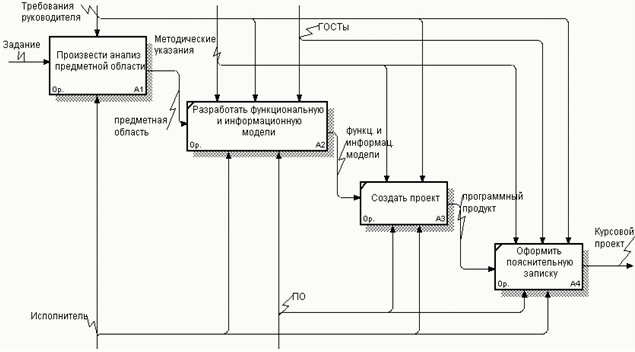
Рис.3.9 — Блок «Создать курсовой проект»

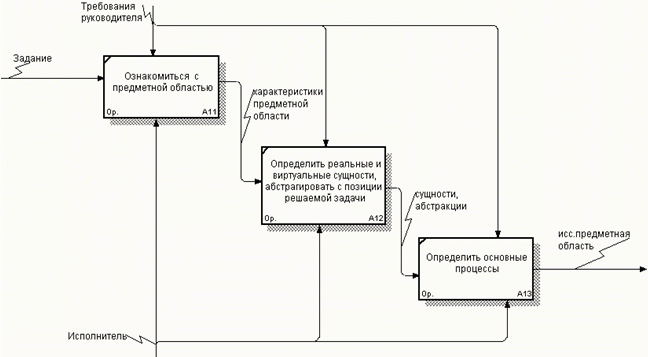
Рис.3.10 — Декомпозиция блока «Произвести анализ предметной области»

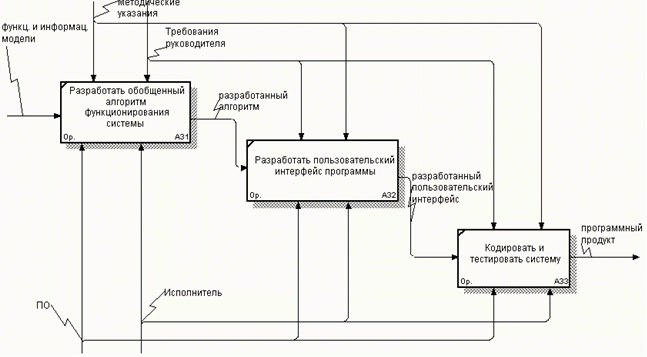
Рис.3.11 — Декомпозиция блока «Создать проект»

Лекция 4: Математическое описание систем (1 часть)

Рассмотренные на предыдущей лекции примеры свидетельствуют о том, что абстрактная характеристика данной системы может быть получена с помощью полезных типов математического описания. Однако при этом естественно возникает вопрос: а для чего вообще нужно какое-либо математическое описание? Ответ на этот вопрос в значительной степени связан с нетривиальностью современных научных результатов и необходимостью уметь выделять существенные свойства описательных моделей. Кроме того, использование именно математического описания обусловлено следующими важными соображениями:

• Компактность. Словесное (или вербальное) описание системы (или процесса), как правило представляет собой нагромождение нечетких высказываний, которые лишь затуманивают существо дела. Избавиться от таких нечетких и не до конца продуманных соображений помогает компактная математическая символика. Математическое описание дает нам аналог знакомой картины и оказывается информативнее любого словесного описания.

• Ясность. Использование математического описания позволяет каждому аспекту изучаемого процесса поставить в соответствие определенный математический символ, в результате чего становится нагляднее взаимосвязь, существующая между различными параметрами процесса. Более того, подобное сопоставление позволяет гораздо проще, чем словесное описание, установить, не были ли упущены какие-либо существенные переменные, или, напротив, не были ли внесены какие-либо дополнительные несущественные сложности при построении описания.

Возможность численного анализа. Как только сделан выбор какого-либо математического описания, последнее «начинает жить» собственной жизнью, более или менее независимой от самого исследуемого процесса.

Другими словами, математическим описанием можно манипулировать в соответствии с обычными законами логики в надежде получить нетривиальное представление о самой системе. Кроме того, математическая модель дает основу для численного анализа, с помощью которого могут быть получены данные не только описательного, но и прогностического характера. Рассмотрим кратко некоторые типы математического описания, которые чаще других используются в математических конструкциях больших систем.

Внутреннее описание

Со времен Ньютона динамические процессы описывали на языке дифференциальных (или разностных) уравнений, т.е. в терминах некоторых естественно выбранных переменных, таких как положение, температура, скорость и т.д. В общем виде такое описание может быть представлено как:

dz/dt = f[z(t), x(t), t], z(0) = z₀, y(t) = h[z(t), x(t), t],

где z(t) — n-мерный вектор, компоненты которого описывают состояние системы в момент времени t; y(t) — p-мерный вектор наблюдаемых выходов системы; x(t) — m-мерный вектор входов системы, z₀ — начальное состояние системы.

В дискретном времени динамика системы может быть описана с помощью разностных соотношений

z(k+1) = F[z(k), x(k), k], z(0) = z₀, y(k) = H[z(k), x(k), k].

Наиболее важным свойством такого описания является то, что оно дает нам представление о поведении системы в некоторой локальной окрестности текущего состояния. При этом неявно предполагается, что локальная информация может быть каким-то образом «собрана воедино», что позволит понять глобальное (во времени или пространстве) поведение системы. Такой подход оказался достаточно обоснованным для анализа многих физических и технических задач. Простые примеры локального описания можно найти в элементарной физике. Известно, например, что колебательное движение груза (маятника) единичной массы, подвешенного на нерастяжимой и невесомой нити единичной длины, описывается уравнением (4.1):

d²z/dt² + a⋅dz/dt + sin(z) = x(t)

где а — коэффициент трения, x(t) — внешня сила, действующая на груз, z(t) — отклонение груза от положения равновесия.

Таким образом, уравнение (4.1) описывает мгновенное изменение положения и скорости маятника как функцию его текущего состояния (положения) и скорости, т.е. мы имеем локальное описание в координатах «положение-скорость», что характерно для всех описаний динамических процессов на языке дифференциальных или разностных уравнений.

Интересно отметить, что математические описания такого типа начали использовать только со времен Ньютона. До этого при описания физических процессов придерживались точки зрения, высказанной Аристотелем, согласно которой важность целого превыше важности его составляющих. Другими словами, значимость элементов, составляющих некоторое множество, трактовалась через значимость самого множества как целого. Однако возможность использования такого подхода в случае менее изученных объектов, в особенности систем социально-экономической природы, вовсе не очевидна.

Взгляды Аристотеля господствовали в физике на протяжении многих столетий, пока Галилей не высказал иную точку зрения, которая впоследствии была обоснована Ньютоном: целое объясняется свойствами его элементарных (локальных) составляющих, так называемый холистский подход. Сложность современной жизни, проявляющаяся в политике, экономике, социологии стимулирует возрождение интереса к холистским теориям.

Внешнее описание

Тип математического описания, с которым чаще всего приходится иметь дело ученому-экспериментатору, — это связь «вход-выход». Во многих отношениях такое описание диаметрально противоположно частному, локальному описанию, поскольку оно не содержит деталей и единственным доступным источником информации является закономерность (отображение), связывающая выходы системы с ее входами. При этом ничего не известно о внутреннем механизме преобразования входов в выходы. По этой причине связь вход-выход часто называют «внешним описанием» системы в отличие от «внутреннего» (или локального) описания (см. рис.4.1).

Внутреннее и внешнее описания позволяют рассматривать систему как устройство, образующее входы и выходы в соответствии с правилами, определенными внутренним описанием. Иными словами, система является информационным процессом в некотором обобщенном смысле.

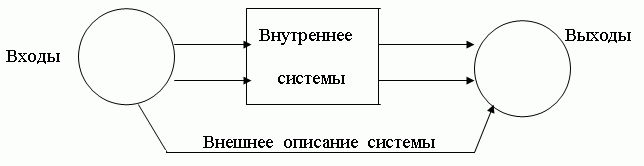
Рис.4.1 — Внешнее и внутреннее описание системы

Очевидно, что внутреннее описание говорит нам гораздо больше о способе действия системы, поскольку каждое такое описание порождает внешнее описание. Тем не менее построение модели системы часто связано с решением диаметрально противоположного вопроса: может ли внутренняя модель «объяснить» каждое внешнее описание? Ответом на этот вопрос по существу является решение так называемой «задачи реализации», которая представляет собой один из важнейших аспектов теории систем.

Наиболее «сырая» возможная ситуация, при которой возникает необходимость в описании типа «вход-выход», имеет место, когда мы располагаем всего лишь таблицей элементов (часто чисел), характеризующих реакцию (выходы) системы на различные внешние воздействия (входы). В этом случае внешнее описание системы эквивалентно отображению:

f: X → Y,

где через X обозначено множество возможных входов, а через Y множество возможных выходов системы. Как отмечалось во многих задачах (в частности, психологии, экономики и общественных наук) множества X и Y представляют собой конечный набор элементов, связь между которыми описывается с помощью функции f.

Пример

Предположим, что эксперт, изучающий «черный» ящик не имеет ни малейшего представления ни о его природе, ни о его содержимом. Вместе с тем эксперт может производить над ним некоторые действия (входы) и наблюдать их результаты (выходы). Предположим для определенности, что элементами множества X и множества Y являются показания различных измерительных приборов. Тогда описание эксперимента типа «вход-выход» могло бы быть таким:

Время	Вход	Выход
10:05	Эксперт не производит никаких действий	Прибор издает звуковой сигнал частотой 240 Гц
10:06	Эксперт нажал на кнопку «A»	Частота сигнала возросла до 480 Гц
10:07	Эксперт случайно нажал на кнопку «B»	Ящик нагрелся на 20°C и начал вибрировать

Этот довольно тривиальный пример показывает, что входы и выходы системы являются функциями времени, т.е. нельзя один и тот же эксперимент провести дважды! Единственное, что можно сделать, — это провести следующий эксперимент, который хотя и незначительно, но будет отличаться от предыдущего.

Менее тривиальный пример внешнего описания системы дает «бихевиористская» школа психологов, для которой характерным является проведение эксперимента и запись его результатов в формате «воздействие-реакция». По мнению представителей этой школы, такое внешнее описание системы дает максимум информации, которую вообще можно получить о ее структуре и функционировании. В то же время «познавательная» школа придерживается другой точки зрения, утверждая, что единственным удовлетворительным описанием системы может быть только внутренняя модель.

Основываясь на довольно общих результатах теории систем, можно показать, что это спор ни о чем. Обе школы, в сущности, утверждают одно и то же, и с точки зрения теории систем эти дебаты столь же содержательны, как и дискуссии относительно того, какая сторона монеты наиболее полно отражает ее стоимость.

Описание систем с конечным числом состояний

В тех случаях, когда предположение конечномерности пространства состояний заменяется предположением о конечности числа его элементов, мы имеем дело с классом систем, анализ которых возможен с помощью чисто алгебраических методов. Важность такой замены трудно переоценить, поскольку совокупность систем с конечным числом состояний включает все последовательные цифровые вычислительные машины.

Математическое описание системы с конечным числом состояний включает:

• множество допустимых входов — X,

• множество допустимых выходов — Y,

• множество состояний — Z,

• функцию перехода — : Z X Z,

• функцию выхода — : Z X Y,

При этом предполагается, что множества X, Y и Z конечны. Это позволяет представить описание системы в виде:

[.] = (X, Y, Z, η σ).

В литературе такое представление часто называют схематическим.

Как отмечалось, ограничения вычислительного характера с неизбежностью вынуждают нас явно или неявно сводить каждую системную задачу к виду, указанному выше. Поэтому необходимы тщательное изучение и понимание алгебраической структуры подобных «конечных» описаний, которая основывается на теории конечных полугрупп. Рассмотрение этой теории выходит за рамки настоящего курса лекций.

Пример

Пусть система состоит из симметрий вращения правильного треугольника. Тогда некоторые возможные конечные пространства состояний могут иметь вид:

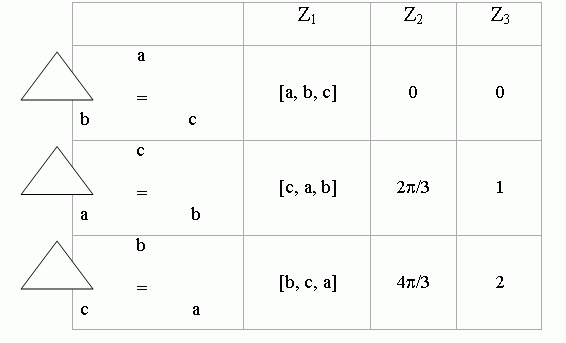
Рис.4.2 — Конечные пространства

Для описания системы достаточно любого из этих пространств состояний, однако только некоторые из них удобнее использовать для вычислений результата воздействия на состояние системы. Следовательно, пространство состояний вовсе не обязательно должно быть непосредственно привязано к реальному физическому процессу. Это чисто математическая условность, введенная для упрощения проблемы определения реакции системы на заданные внешние воздействия.

Пусть имеются два возможных отображения σ₁ и σ₂, переводящие одно состояние системы в другое и соответствующие повороту треугольника вокруг центра тяжести на 120 и 240 градусов соответственно. Результаты применения этих отображений к различным пространствам состояний можно представить в виде таблицы:

	zi	σ1(zi)	σ2(zi)
z1 →	[a, b, c] [c, a, b] [b, c, a]	[c, a, b] [b, c, a] [a, b, c]	[b, c, a] [a, b, c] [c, a, b]
z2 →	0 2π/3 4π/3	2π/3 4π/3 0	4π/3 0 2π/3
z3 →	0 1 2	1 2 0	2 0 1

Пространство z₁ на первый взгляд излишне сложное, оказывается вполне пригодным для более сложных систем, например в случае симметрий более общего вида, где могут присутствовать отображения типа σ. В то же время пространства z₂ и z₃ не допускают очевидных обобщений на более сложные случаи с сохранением простоты вычислений.

Способ выбора конкретного пространства состояний системы называется ее координатизацией. При этом важно установить, всегда ли существует координатизация, которую можно считать «хорошей» с точки зрения описания поведения системы. Ключевым моментом проблемы координатизации является алгебраическая структура модели системы в пространстве состояний.

Лекция 5: Математическое описание систем (2 часть)

Энтропия и потенциальная функция При изучении систем с информационно-теоретической точки зрения часто ее описание дается на языке энтропии и потенциальных функций. По аналогии с классической механикой и теорией поля можно рассматривать реакцию системы на внешнее воздействие как динамическое изменение состояния системы, в процессе которого она стремится минимизировать некоторую потенциальную функцию. В зависимости от конкретного вида системы и принятых допущений такая динамика может быть локальной в смысле движения системы к относительному минимуму, ближайшему к текущему состоянию, или глобальной в смысле движения к абсолютному (глобальному) минимуму соответствующей потенциальной функции.

Приближенное описание динамического процесса на языке потенциальных функций включает следующие составляющие:

• пространство состояний (фазовое пространство) Z;

• набор входных функций X;

• гладкое отображение f: Z*X → R;

где R — есть пространство действительных чисел.

При этом предполагается, что система ведет себя так, что при фиксированном входе x ее н аблюдаемое состояние соответствует локальному либо глобальному минимуму потенциальной функции.

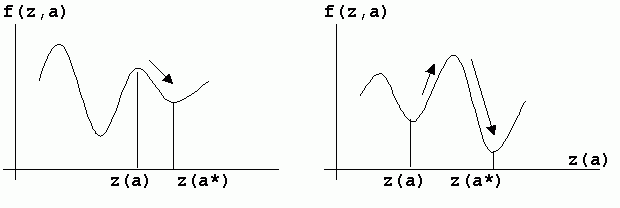
Рис.5.1 — Потенциальная функция системы

А) — движение к локальному минимуму; В) — движение к глобальному минимуму; f(z,a) — потенциальная функция; z(a) —  начальное положение системы, где а — внешний параметр.

Замена параметра а на а* приводит к изменению положения минимума функции f(z,a).

Использование потенциальной функции для описания хорошо изученных физических систем оказалось весьма удачной альтернативой внутренних описаний. Успешное применение такого подхода в классической физике обусловлено существованием незыблемых вариационных принципов, таких как принципы Гамильтона, Ферма и Даламбера. В большинстве случаев внутреннее описание физического процесса на языке потенциальных функций естественным образом вытекает из описания с пoмощью потенциальных функций в силу уравнений Гамильтона-Якоби и Эйлера-Лагранжа.

В системах, которые являются предметом изучения общественных наук, возможность использования такого описания не столь обоснована из-за сложности применения вариационных принципов. Однако в ряде случаев при анализе устойчивости или в теории катастроф знание точного вида потенциальной функции не является необходимым для определения важных качественных свойств системы — важен лишь сам факт ее существования.

С описанием системы на языке потенциальных функций тесно связана идея описания поведения систем с помощью энтропии. Как известно из классической термодинамики, энтропия является мерой беспорядка, существующего в данной физической системе. Мерой упорядоченности системы является отрицательная энтропия или негэнтропия. В основе описания динамического процесса с помощью энтропии лежит предположение преобразовании негэнтропии входа в информацию. Это означает, что все замкнутые системы изменяются таким образом, что минимизируют изменение энтропии. Таким образом, становится очевидной связь между описанием на языке потенциальных функций и энтропии.

Чтобы показать общность описаний в терминах энтропии, перечислим основные аксиомы релятивистской теории информации, развитой Джюмэри для динамических процессов.

Аксиома 1. Система является частью некоторой вселенной и развивается только постольку, поскольку она преследует некоторую цель.

Аксиома 2. Для достижения цели система воспринимает информацию I из окружающей среды и использует эту информацию для перестройки собственной организации (внутренней структуры) A, в результате которой увеличилась бы негэнтропия n, и для оказания воздействия L на окружающую среду.

Аксиома 3. (Принцип эволюции). Структурная энтропия Е системы определяется соотношением dE = dI/n и является неубывающей функцией эволюции.

Аксиома 4. Вселенная не может наблюдать собственную эволюцию. В силу этих аксиом уравнение состояния системы имеет вид:

f(H_e, H_i, ν) = 0, где

• H_e — внешняя энтропия системы по отношению к фиксированному наблюдателю R,

• H_i — внутренняя энтропия системы по отношению к наблюдателю R,

• ν — цель системы с точки зрения наблюдателя R.

При таком подходе к описанию системы наблюдатель (или лицо, принимающее решение) играет особую роль, причем особый упор делается на кинематический подход, основанный на аналогах преобразования Лоренца для двух наблюдателей R и R*.

Анализируя уравнение состояния, можно заметить, что знание функции f позволяет вычислить структурную энтропию Е c помощью соотношения, описывающего обмен информацией:

dI = α⋅dH_e + β⋅dH_i

Пример 1. Одномерная динамика

Рассмотрим простую динамическую систему x(t) = u(t),

где x(t) и u(t) — скалярные функции. Поскольку внешняя энтропия H_e обладает теми же свойствами, что и время t, произведем замену: t H_e. Более того, имеет смысл отождествить внутреннее состояние x с внутренней энтропией H_i. Тогда динамика системы эквивалентным образом описывается уравнением

dH_i - u(H_e)⋅dH_e = 0

Попытаемся теперь построить функцию состояния f в соответствии с приведенным выше ее определением. Из равнения состояния следует, что

df/dH_e⋅dH_e + df/dH_i⋅dH_i + df/dν⋅dν = 0

Не имея дополнительной информации о системе, можно предположить, что ее цель не меняется.Интегрируя уравнение динамики, получаем

f(H_i, H_e, ν) = H - ∫u(s)ds = 0

где H_e0 — внешняя энтропия в начальный момент времени t₀.

Проведенный анализ показывает, что система x = u не определена с точки зрения обмена информацией с окружающей средой. Более того, такой обмен вообще не имеет места.

Пример 2. Стационарная динамика

Рассмотрим систему, описываемую уравнением

x(t) = Ψ[X(t)]

которое способом, аналогичным рассмотренному в примере А, можно привести к виду

dH_i - Ψ(H_i)dH_e = 0

Чтобы получить уравнение состояния, следует записать

df/dH_i = 1 ⇒ f = H_i + k(H_e)

df/dH_e = Ψ(H_i) ⇒ Ψ(H_i) = f(H_e)

Однако эти уравнения противоречивы и уравнение динамики следует рассматривать не как уравнение состояния, а как уравнение обмена информацией

dI = dH_i - Ψ(H_i)dH_e = 0

Следовательно, система не обменивается информацией с окружающей средой и развивается с постоянной структурной энтропией, что находится в соответствии с автономным характером системы.

В целом можно сказать, что «энтропийный» подход к анализу систем основан на трактовке системы, как некоторого единого целого. Отсюда следует, что понять сущность системы можно, лишь изучая ее взаимодействие с окружающей средой, т.е. с некой «вселенной». Взгляд на систему как на единое целое можно развить, введя понятие «связь». Весь комплекс связей и их характеристик приводит к понятию «структура» и «сложность» системы.

Множества и отношения

Рассмотрим теперь тип описания систем, который оказывается особенно эффективным при таких структурных исследованиях. Принято считать, что математическими абстракциями в основном оперирует теория множеств и отношений между их элементами. Поэтому целесообразно попытаться определить понятие системы в терминах этой теории. От конструктивного определения, естественно, можно потребовать, чтобы элементы соответствующих множеств и связывающие их отношения определялись спецификой конкретной системы. Тем не менее, если мы построим даже такое «специализированное» описание системы, оно даст весьма широкие возможности для анализа не только структуры системы, но и ее поведения в динамике.

В общем случае можно предположить, что существуют два конечных множества X и Y, элементы которых как-то связаны с системой. Это могут быть множества хищников и их жертв, множества типов автомобилей и дорог или множества предприятий службы быта и предлагаемых услуг. Для описания связи, существующей между двумя элементами (x,y) введем на прямом произведении X и Y бинарное отношение

λ, λ ∈ X×Y

Рассмотрим тривиальный пример, в котором X есть множество товаров, а Y — множество предприятий службы быта. Пусть для определенности

X = {x₁(хлеб), x₂(молоко), x₃(марки), x₄(обувь)}

Y = {y₁(гастроном), y₂(универмаг), y₃(банк), y₄(почта)}

Определим отношение A на прямом произведении X Y следующим образом:

Отношение A существует между x_i и y_j тогда и только тогда, когда x_i можно купить в y_j. В этом случае

λ = {(x₁,y₁), (x₂,y₁), (x₃,y₄), (x₄,y₂)}

Отношение A удобно представить матрицей инциденций:

λ	y1	y2	y3	y4
x1	1	0	0	0
x2	1	0	0	0
x3	0	0	0	1
x4	0	1	0	0

[Λ]_ij = 1, (x_i, y_j) ∈ λ

С геометрической точки зрения отношение A определяет симплициальный комплекс KX(Y;A), в котором элементы множества Y рассматриваются как вершины, а элементы множества X являются симплексами. Так элемент x₁(хлеб) является 0-симплесом, состоящим из вершины y₁(гастроном). Если К не содержит r-симплексов (r ≥ 3), его можно изобразить на плоскости.Для предыдущего примера множество К имеет вид y₁ y₂ y₄...

Хотя такая геометрическая структура не представляет особого интереса, тем не менее она все же показывает, что комплекс не содержит связных компонент и что вершина y₃(банк) не играет никакой роли в анализе КX(Y;A).

Определив подходящие множества X и Y и отношение A, можно перейти еще к одному отношению. Это так называемое сопряженное отношение A*, которое получается, если поменять местами множества X и Y, и строится в соответствии с правилом: отношение A* существует между y_i и x_j тогда и только тогда, когда между x_j и y_i существует отношение A.

Матрица инциденций для A* получается транспонированием матрицы инциденций для A, т.е. A* = A×1. В результате получим геометрический комплекс КY(X;A*), в котором Х — множество вершин, а Y — множество симплексов. Тогда для рассмотренного выше примера комплекс имеет вид

который конечно же более содержателен, чем полностью несвязная структура КX(Y;): вершины x₁(хлеб) и x₂(молоко) связаны 1-симплексом (гастроном).

Продемонстрируем общность описания систем на языке множеств и бинарных отношений еще на одном примере.

Пример

Шахматы. Чемпион мира по шахматам Эммануил Ласкер как то заметил: «Если из 64 клеток шахматной доски вы контролируете 33, то преимущество на вашей стороне». Для нас данное высказывание представляет особый интерес, так как оно свидетельствует о том, что главное для шахматиста — это «стратегическое» содержание игры, которое мы можем выразить непосредственно в виде отношения между множеством фигур и множеством клеток шахматной доски.

Рассмотрим два отношения Aw и Ab, где Aw определяет связь между белыми фигурами и клетками доски, а Ab- та же связь для черных фигур.

Определим множества X и Y как

X = { фигуры }

X = { QR, QN, QB, Q, K, KB, KN, KR, QRP, QNP, QBP, QP, KP, KBP, KNP, KRP},

Y = { клетки }.

Мы здесь использовали стандартные международные обозначения для фигур: король — К, ферзь — Q, слон — В, конь — N, ладья — R, пешка — Р. При этом предполагается, что клетки доски также упорядочены соответствующим образом. Имеются в виду также следующие обозначения: буква Q в двухбуквенных символах означает ферзевый фланг, а К — королевский. Средняя буква в трехбуквенных символах (для пешек) обозначает фигуру, перед которой стоит данная пешка в начальной позиции.

Пусть заданы x_i и y_j; определим отношение Aw следующим образом:

(x_i, y_j) ∈ λw

тогда и только тогда, когда фигура x_i атакует клетку y_j. Под термином «атакует» понимается одна из следующих ситуаций:

• Если ход белых и если фигура x_i не пешка и не король, то ход x_i y_j — правильный (разрешенный) ход.

• Если фигура x_i пешка, то клетка y_i находится под боем со стороны фигуры x_i

• Если клетка y_j занята белой фигурой, то фигура x_i защищает эту фигуру.

• Если фигура x_i — белый король, то клетка y_j является соседней клеткой по отношению к клетке, занимаемой фигурой x_i.

• Если клетка y_j занята черной фигурой (но не королем) и если ход белых, то взятие данной черной фигуры фигурой x_i — правильный ход.

• Черный король занимает клетку y_j и находится под шахом фигуры x_i.

Аналогично определяется отношение Ab.

Отметим, что Aw зависит от состояния игры (от расположения фигур на доске и от того, чей ход).

На этом рассмотрения настоящего примера заканчивается. Слушателю предоставляется возможность самостоятельно построить матрицы инциденций Aw и Ab.

Внимательный слушатель, несомненно, заметил некоторое сходство между теоретико-множественным описанием системы и более привычным описанием в терминах теории графов на языке узлов и дуг (или вершин и ребер). По существу, данное выше определение совпадает с описанием на языке теории графов, если определить X, Y как множества вершин, соединенных ребрами в соответствии с отношением A. Хотя при таком переходе в значительной степени утрачивается его гибкость, так при этом исчезает (в лучшем случае затушевывается) универсальность отношения A, тем не менее оно оказывается полезным во многих ситуациях.

Для теории систем наиболее существенным является описание динамики систем. Поэтому, чтобы понять, каким образом динамические переходы учитываются при теоретико-множественном описании процесса (системы) введем понятие образ. Вообще говоря, образ П есть отображение, которое каждому симплексу из комплекса ставит в соответствие определенное число, т.е.

П: σ_i → k

где К-определенная система чисел(действительных,целых и т.д.)

Поскольку каждый симплекс из К обладает некоторой геометрической размерностью, которая определяется числом его вершин, то образ П является ранжированным образом

П = П₀⊕П₁⊕...⊕П_N

где N = dim K — размерность наибольшего симплекса из К. Здесь каждое П_i является отображением, определенным только на множестве i-мерных симплексов из К.

Поясним понятие образа на примере «хищник-жертва». Напомним, что мы ввели два множества X — множество жертв и Y — множество хищников с матрицей инциденций:

λ	x1	x2	x3	x4	x5	x6	x7	x8
y1	1	1	1	1	0	0	0	0
y2	1	0	1	0	0	0	0	0
y3	0	0	0	0	1	1	0	0
y4	0	1	0	0	1	0	1	1
y5	0	0	0	0	0	0	1	0
y6	0	1	0	0	1	0	0	0

Таким образом, y₁(люди) — это 3-симплекс, y₄(птицы) -3-симплекс и т.д. Образ П при этом ставит в соответствие каждому симплексу некоторое число, скажем численность популяции в данный момент. Поскольку симплексы ранжированы по их размерности, то и П_i также ранжированы,

поэтому в каждый момент:

П₀: {y5(рыбы)} — численность рыб, {y₂(львы)} — численность львов

П₁: {y₃(слоны)} — численность слонов, {y6(лошади)} — численность лошадей

П₂: — пусто

П₃: {y₁(люди)} — численность народонаселения, {y₄(птицы)} — численность птиц

Полный образ для данной экосистемы имеет вид

П = П₀⊕П₁⊕П₃

Динамику системы можно теперь описать изменениями образа П в каждый момент времени.