Лекция 22: Решение хорошо структуризованных проблем
Для решения проблем этого класса широко используются математические методы И.О. В операционном исследовании можно выделить основные этапы:
Определение конкурирующих стратегий достижения цели.
Построение математической модели операции.
Оценка эффективностей конкурирующих стратегий.
Выбор оптимальной стратегии достижения целей. Математическая модель операции представляет собой функционал
E = f(x∈x^, {α}, {β})⇒ extz
Е — критерий эффективности операций;
x — стратегия оперирующей стороны;
a — множество условий проведения операций;
b — множество условий внешней среды.
Модель позволяет оценить эффективность конкурирующих стратегий и выбрать из их числа оптимальную стратегию.
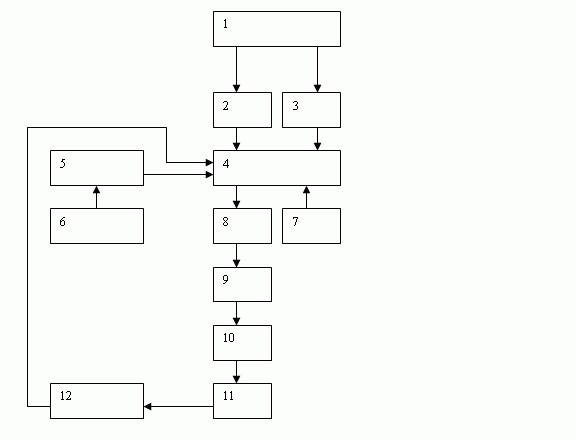
Рис. 22.1 — Выбор оптимальной стратегии достижения целей
постоянство проблемы
ограничения
критерий эффективности операций
математическая модель операции
параметры модели, но часть параметров, как правило, не известна, поэтому (6)
прогнозирование информации (т.е. нужно предугадать ряд параметров)
конкурирующие стратегии
анализ и стратегии
оптимальная стратегия
утвержденная стратегия (более простая, но которая удовлетворяет еще ряду критериев)
реализация решения
корректировка модели
Критерий эффективности операции должен удовлетворять ряду требований:
Представительность, т.е. критерий должен отражать основную, а не второстепенную цель операции.
Критичность — т.е. критерий должен изменяться при изменении параметров операций.
Единственность, так как только в этом случае возможно найти строгое математическое решение задачи оптимизации.
Учет стохастичности, которая связана обычно со случайным характером некоторых параметров операций.
Учет неопределенностей, которая связана с отсутствием какой-либо информации о некоторых параметров операций.
Учет противодействия, которое вызывает часто сознательный противник, управляющий полными параметрами операций.
Простая, т.к. простой критерий позволяет упростить математические выкладки при поиске opt. решения.
Приведем схему, которая иллюстрирует основные требования к критерию эффективности исследования операций.
Рис. 22.2 — Требования к критерию эффективности исследования операций
постановка проблемы (вытекают 2 и 4 (ограничения));
критерий эффективности;
задачи верхнего уровня
ограничения (мы организуем вложенность моделей);
связь с моделями верхнего уровня;
представительность;
критичность;
единственность;
учет стохастичности;
учет неопределенности;
учет противодействия (теория игр);
простота;
обязательные ограничения;
дополнительные ограничения;
искусственные ограничения;
выбор главного критерия;
перевод ограничений;
построение обобщенного критерия;
оценка математического отид-я;
построение доверительных интервалов:
анализ возможных вариантов (есть система; мы точно не знаем, какова интенсивность вх. потока; мы можем только с определенной вероятностью предположить ту или иную интенсивность; затем взвешиваем выходящие варианты ).
Единственность — чтобы можно было решить задачу строго математическими методами.
Пункты 16, 17 и 18 — это способы, которые позволяют избавиться от многокритериальности.
Учет стохастичности — большая часть параметров имеет стохастическое значение. В ряде случаев стох. мы задаем в виде ф-и распределения, следовательно, сам критерий необходимо усреднить, т.е. применять математические ожидания, следовательно, п.19, 20,