4.2 Теорема Вариньона

Не всегда модуль момента силы относительно центра легко найти. Рассмотрим следующий пример (рис.4.5). Сила приложена в точке А. Необходимо найти момент силы относительно центра О. Однако определить плечо h зная только координаты точек А и О затруднительно. Поэтому воспользуемся теоремой Вариньона.

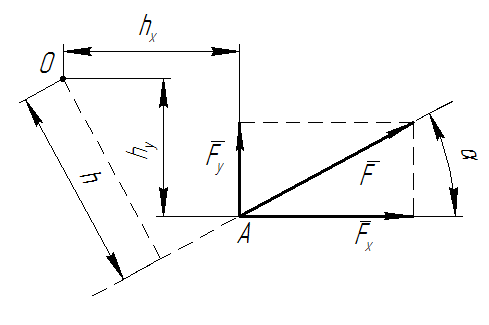
Рисунок 4.5

Теорема Вариньона. Момент равнодействующей относительно любой точки равен геометрической сумме моментов составляющих сил относительно этой точки.

Разложим силу F на составляющие F_x, F_y.

Сила F для сил F_x и F_y будет является равнодействующей, тогда согласно т. Вариньона:

Следует учитывать, что знаки моментов от сил F_x и F_y могут быть различными. В нашем примере моменты положительны:

Представленный метод широко используется при решении задач.

4.3 Момент силы относительно оси

Момент силы относительно центра является величиной векторной. Соответственно, как и любой вектор его можно спроецировать на оси координат.

Из векторной алгебры известно, что векторное произведение можно представить определителем:

(4.3)

где х, у, z – проекции вектора ;

X, Y, Z – проекции вектора на оси координат;

i, j, k – единичные орт-вектора.

Полученный результат можно представить в виде:

,

где М_x, M_y, M_z – проекции момента силы на оси координат или моменты силы относительно осей x, y и z.

, , (4.4)

В общем случае момент силы относительно любой оси n можно найти по следующему правилу. Необходимо спроецировать силу F на плоскость N, перпендикулярную оси n, а затем вычислить момент ее проекции F₁ на эту плоскость относительно точки О пересечения оси n с плоскостью N, приписав этому моменту знак плюс или минус (рис.4.6).

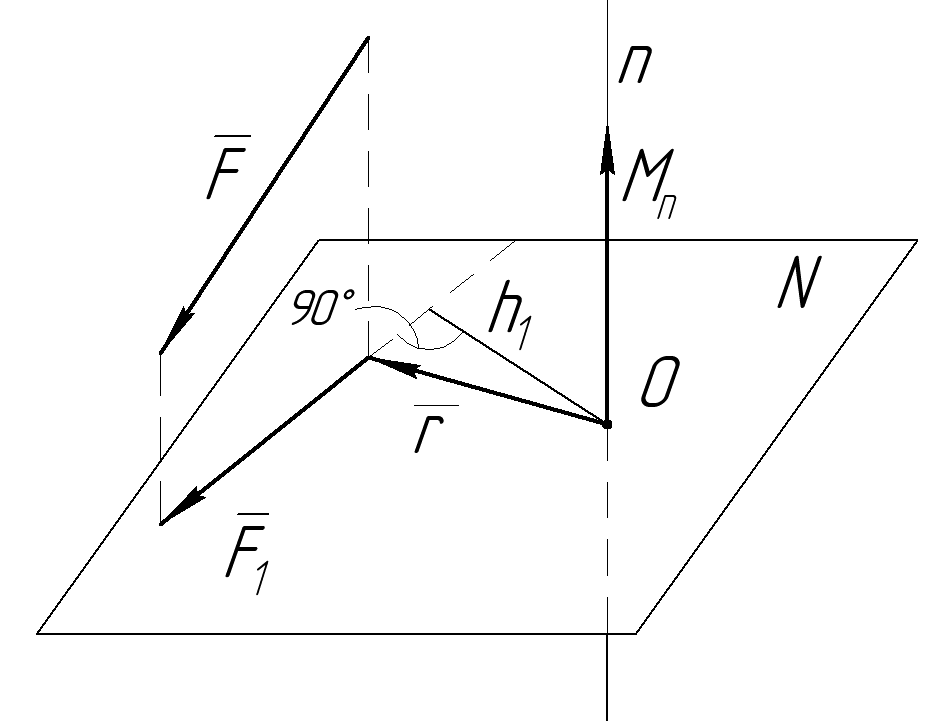
Рисунок 4.6

Если сила вращает вокруг оси против часовой стрелки (смотрим со стороны стрелки оси), то момент положителен. И отрицателен, если наоборот.

Момент силы относительно оси равен нулю в двух случаях:

1) если F₁=0, т. е. линия действия силы параллельна оси;

2) сети h₁=0, т. е. линия действия силы пересекает ось. Отсюда следует: если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю.

4.4 Пара сил

Рассмотрим теперь действие на тело двух равных по модулю, параллельных и противоположно направленных сил (рис. 4.7).

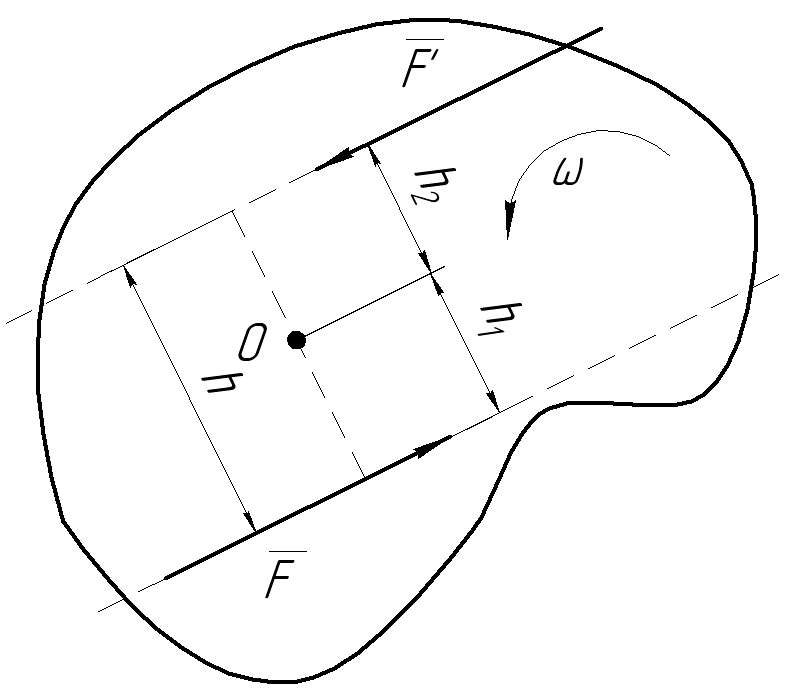
Рисунок 4.7

В отличие от предыдущего случая (рис. 4.1) тело не будет совершать поступательного движения. Так как F и F’ равны по модулю, но противоположно направлены, то их сумма будет равна “0”. Однако момент относительно любого центра будет равен:

(4.5)

т.к. F=F’, то

(4.6)

В результате силы стремятся вращать тело.

Данная система сил равных по модулю, параллельных и противоположно направленных называется парой сил. Плоскость, в которой расположены силы F и F’ называется плоскостью действия пары. Силовой характеристикой действия пары является момент. Модуль момента определяется по формуле (4.6). Плечом пары h называется наикратчайшее расстояние между линиями действия сил. Знак момента и направление вектора момента определяется таким же образом, как и для момента силы относительно центра.

Пары с одинаковым моментом называются эквивалентными (равными). Важным свойством пары является то, что, не изменяя оказанного действия на тело, пару можно переносить в любую точку тела, как в плоскости действия пары, так и параллельно. При этом можно произвольно менять значение составляющих пару: модуль сил и плечо, однако при этом момент пары должен оставаться постоянным.