3.3 Пример решения задачи с1

Задание. Конструкция состоит из невесомых стержней 1, 2, …6, соединенных друг с другом (в узлах K и М) и с неподвижными опорами A, B, C, D шарнирами (рис. 3.7). В узлах K и М приложены силы P и Q, образующие с координатными осями углы α₁, β₁, γ₁ и α₂, β₂, γ₂ соответственно.

Рисунок 3.7

Дано: P=100Н, α1=60º, β1=60º, γ1=45º, Q=50Н , α2=45°, β2=60º, γ2=60º, ψ=30º, φ=60º, δ=74º. Определить усилия в стержнях 1-6.

Решение.

Разложим силы P и Q на составляющие (проекции сил на оси). Так как сила P составляет с координатными осями углы (рис.3.8), то:

Рисунок 3.8

Аналогично для силы Q:

Концы стержней соединены между собой и опорами с помощью шарниров. Силы так же приложены только в узлах (шарнирах). При такой конструкции внутренние усилия, возникающие в стержнях, направлены только вдоль стержней, а они (стержни) подвержены растяжению или сжатию.

Рассмотрим равновесие узла K, в котором сходятся стержни 1, 2, 3. На узел действуют сил P и реакции N₁, N₂, N₃ стержней, которые направим по стержням от узла, предварительно считая стержни растянутыми (рис.3.9).

Рисунок 3.9

Рисунок 3.10

Из рисунка 3.9 видно, что сила N₁ проецируется только на ось y’, сила N₂ на ось x’ и ось y’, а N₃ на оси x’ и z’. Так как x’, y’, z’ параллельны соответствующим осям x, y, z, то и проекции сил на оси будут равны.

Полученная система сил P, N₁, N₂, N₃ является сходящейся системой сил, поэтому воспользуемся выражениями (3.6) и составим уравнения равновесия.

(1)

(2)

(3)

Вначале определим значение N₃ из (3):

Подставив значение N₃ в уравнение (1) найдем N₂:

И, наконец, определим N₁:

Рассмотрим равновесие узла М (рис.3.10). На узел действует сила Q и реакции N₂’, N₄, N₅, N₆. При этом по закону о равенстве действия и противодействия реакция N₂’ направлена противоположно N₂, числено же N₂’=N₂.

Из рисунка 3.10 видно, что сила N₄ проецируется только на ось x”, сила N₆ только на ось z”, а сила N₅ на все оси. Причем, чтобы найти проекцию N₅ на ось x” или ось y” вначале необходимо спроецировать силу на плоскость x”y” (или параллельно ей) – получим N₅sin(δ), и лишь затем проецировать N₅sin(δ) на соответствующие оси.

Система сил Q, N₂’, N₄, N₅, N₆ также является системой сходящихся сил. Составляем уравнения равновесия.

(4)

(5)

(6)

Находим последовательно значения N₅, N₆, N₄.

Из (5)

Из (6)

Из (4)

Ответ: N₁=348,7H; N₂=–344,9H; N₃=141,4H; N₄=50,3; N₅=328,8H; N₆=–65,6H. Знак “–” показывает, что силы направлены в обратную сторону от принятого перед решением задачи. Соответственно стержни 2 и 6 сжаты.

4 Момент

4.1 Момент силы относительно центра

Под действием силы тело может совершать не только поступательное движение, но и вращательное. Рассмотрим два примера действия некоторой силы на тело.

Рисунок 3.1

Случай 1. Сила F приложена к центру тяжести или линия ее действия пересекает центр тяжести тела (Ц.Т.). В этом случае тело будет двигаться только поступательно (прямолинейно) (рис.4.1а).

Случай 2. Линия действия силы смещена от центра тяжести на некоторое расстояние (рис.4.1б). В результате тело будет не только перемещаться в пространстве, но и вращаться вокруг Ц.Т. Вращение будет тем сильнее, чем больше расстояние между линией действия силы F и центром. И наоборот.

Вращательный эффект силы относительно цента характеризуется моментом силы. Момент силы относительно центра является величиной векторной. Модуль момента силы относительно центра определяется произведением модуля силы F на плечо h взятым со знаком “+” или “–”:

(4.1)

Соответственно размерность момента в системе СИ [Н*м].

Плечо h является наименьшим расстоянием от центра до линии действия силы и определяется с помощью перпендикуляра, проведенного из центра к линии действия.

Знак момента принимается по следующему правилу: если сила стремиться повернуть тело относительно точки, для которой определяется момент силы, против часовой стрелки, то момент считается положительным (рис.4.2а); если наоборот, то отрицательным (рис.4.2б). Следует учесть, что моменты силы относительно различных центров может иметь не только различное значение и, но и знак (рис.4.2в).

Рисунок 4.2

Момент силы величина векторная. Вектор момента перпендикулярен плоскости действия момента – плоскости, в которой расположено плечо и вектор силы. Стрелка вектора направлена в сторону смотрящего, если момент стремится вращать против часовой стрелки, и наоборот, если момент стремится вращать по часовой стрелке (рис.4.3а), то вектор направлен от смотрящего (рис.4.3б).

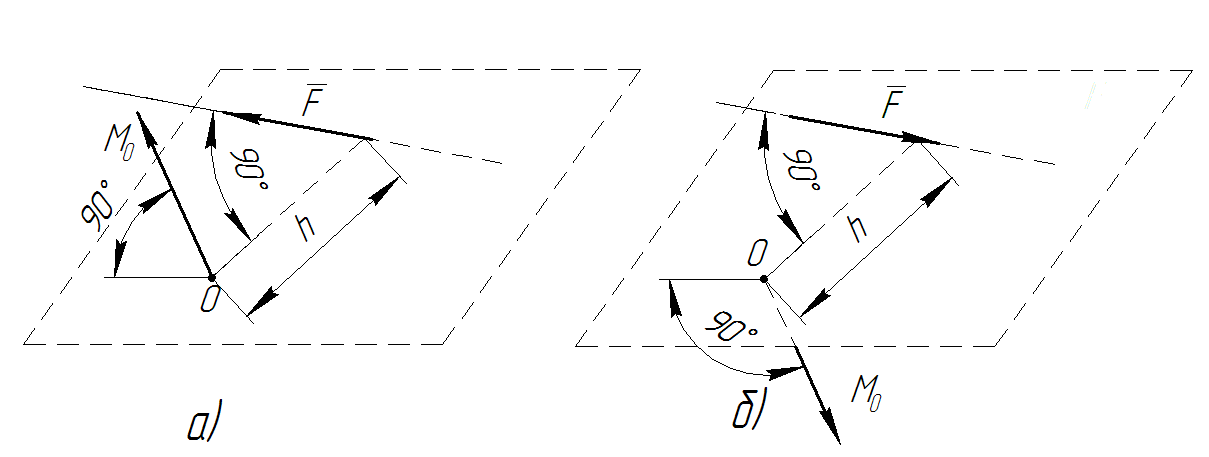
Рисунок 4.3

Вектор момента можно определить при векторном произведении:

, (4.2)

где r – радиус-вектор (вектор из центра О до точки приложения силы F).

Рисунок 4.4