3 Системы сходящихся сил
3.1 Системы сходящихся сил. Определение равнодействующей. Условие равновесия
Сходящимися называются силы, линии действия которых пересекаются в одной точке (рис.3.1а).
Рисунок 3.1
Для определения равнодействующей системы сходящихся сил необходимо и достаточно сложить силы. Сложение можно производить или по правилу параллелограмма (рис.3.1б), последовательно складывая друг с другом векторы сил, или с помощью силового многоугольника (рис. 3.1в), или аналитически.
При аналитическом способе необходимо сложить проекции сил на оси.
Для плоской системы сил:
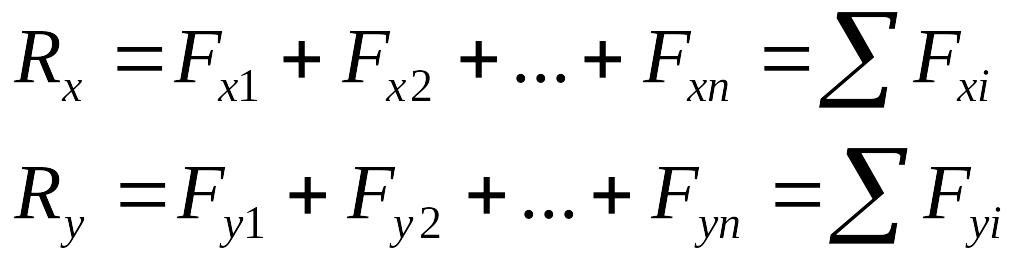(3.1)
Модуль равнодействующей будет равен:
(3.2)
Для пространственной системы сил:
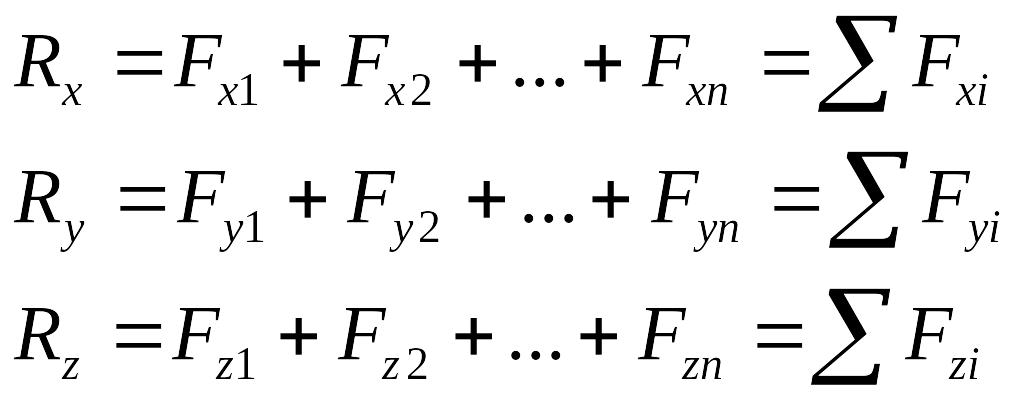(3.3)
Модуль равнодействующей будет равен:
(3.4)
Равновесие системы сходящихся сил. Любое твердое тело, которое находится в покое или движется равномерно и прямолинейно, т.е. не изменяет свое кинематическое состояние, находится в равновесии. Равновесие возможно только тогда, когда действующая на твердое тело система сил будет уравновешена. Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая была равна нулю.
Условие равновесия сходящейся системе сил в векторной форме можно записать следующим образом:
, (3.5)
или для аналитической записи:
(3.6)
3.2 Примеры решения задач
Задача 3.2.1
Определить равнодействующую двух сил F1=50Н и F2=30Н, образующие между собой угол 30° (рис.3.2а).
Рисунок 3.2
Решение.
Перенесем векторы сил F1 и F2 до точки пересечения линий действий и сложим по правилу параллелограмма (рис.2.2б). Точка приложения и направление равнодействующей показано на рисунке. Модуль полученной равнодействующей определим по формуле:
Н
Ответ: R=77,44Н
Задача 3.2.2
Определить равнодействующую системы сходящихся сил F1=10Н, F2=15Н, F3=20Н, если известны углы, образованные векторами этих сил с осью Ох: α1=30°, α2=45° и α3=60° (рис.3.3а)
Рисунок 3.3
Решение.
Проецируем силы на оси Оx и Оy:
Н,
Н,
Н,
Н,
Н,
Н,
Определяем проекции равнодействующей
Н,
Н.
Модуль равнодействующей
Н
На основе полученных проекций определяем направление равнодействующей (рис. 3.3б)
Ответ: R=44,04Н
Задача 3.2.3
В точке соединения двух нитей приложена вертикальная сила P=100Н (рис.3.4а). Определить усилия в нитях, если в состояние равновесия углы образованные нитями с осью OY равны α=30°, β=75°.
Рисунок 3.4
Решение.
Силы натяжения нитей будут направлены вдоль нитей от узла соединения (рис.3.4б). Система сил T1, T2, P является системой сходящихся сил, т.к. линии действия сил пересекаются в точке соединения нитей. Условие равновесия данной системы:
Составляем аналитические уравнения равновесия системы сходящихся сил, проецирую векторное уравнение на оси.
;
;
.
Решаем систему полученных уравнений. Из первого выражаем T2.
,
Подставим полученное выражение во второе и определим T1 и T2.
Н
Н,
Проверим решение из условия, что модуль P’суммы сил T1 и T2 должен быть равен Р (рис.3.4в).
Ответ: T1=100Н, T2=51,76Н.
Задача 3.2.4
Определить равнодействующую системы сходящихся сил, если заданы их модули F1=12Н, F2=10Н, F3=15Н и угол α=60°(рис.3.5а).
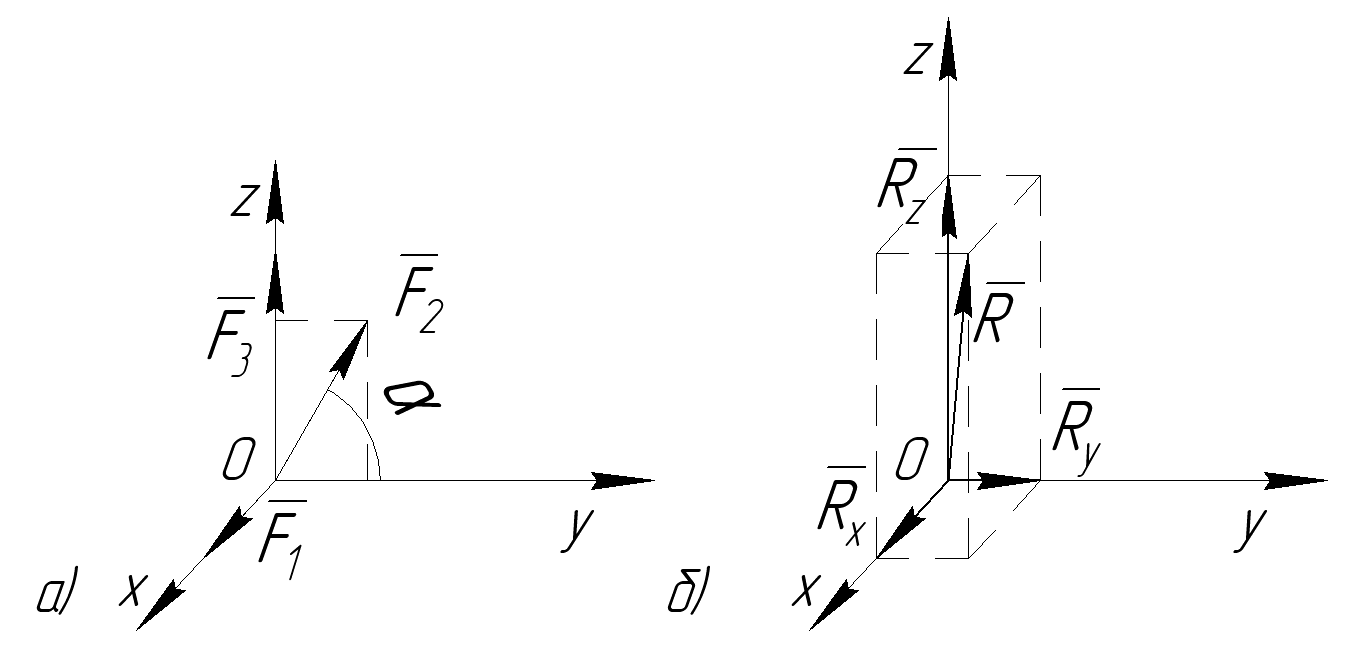
Рисунок 3.5
Решение.
Определяем проекции равнодействующей
Н,
Н,
Н.
Модуль равнодействующей:
Н
На основе полученных проекций определяем направление равнодействующей (рис.3.5б)
Ответ: R=27,17Н
Задача 3.2.6
Три стержня АС, ВС, DC соединены шарнирно в точке C. Определить усилия в стержнях, если задана сила F=50Н, угол α=60° и угол β=75°. Сила F находится в плоскости Оyz. (рис.3.6)
Рисунок 3.6
Решение.
Первоначально предполагаем, что все стержни растянуты, соответственно направляем реакции в стержнях от узла С. Полученная система N1, N2, N3, F является системой сходящихся сил. Условие равновесия данной системы:
Составляем аналитические уравнения равновесия системы.
Силы N1 и F находятся в плоскости перпендикулярной оси Ох, поэтому проекции этих сил на эту ось равны «0».
;
, (1)
;
, (2)
Силы N2 и N3 находятся в плоскости перпендикулярной оси Оz, поэтому проекции этих сил на эту ось равны «0».
;
. (3)
Из (3) определяем N1:
Н.
Знак минус означает, что N1 направлена в обратную сторону. Стержень сжат.
Из
(1)
.
Подставим полученные результаты в (2):
Ответ: N1=-86,6Н, N2=45,52Н, N3=45,52Н.