7 Центр параллельных сил. Центр тяжести твердого тела

7.1 Определение центра параллельных сил и центра тяжести

Системой параллельных сил называется система, линии действия сил которой параллельны друг другу (рис.7.1).

Рисунок 7.1

Очевидно, что равнодействующая R такой системы будет направлена так же, как и силы системы, а по модулю будет равна сумме модулей приложенных сил:

Положение равнодействующей можно определить, зная центр параллельных сил.

Для любой системы параллельных сил существует такая точка, называемая центром параллельных сил, через которую при любом направлении сил проходит линия действия равнодействующей системы.

Координаты центра можно определить по формулам:

, , . (7.1)

где x_i, y_i, z_i – координаты приложения силы F_i.

Примером параллельных сил могут являться силы притяжения отдельных частиц тела к Земле. Силы притяжения направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Равнодействующая этих параллельных сил, является весом тела, а центр системы называется центром тяжести тела.

В твердом теле центр тяжести занимает вполне определенное положение, которое не зависит от расположения рассматриваемого тела в пространстве. Координаты центра тяжести твердого тела определяются по формуле (7.1), заменяя силы на силы тяжести:

, , , (7.2)

где G_i – сила притяжения i-ой частицы тела;

G – вес всего тела.

Несколько преобразовывая формулу можно определять центры тяжести плоских фигур:

, , , (7.3)

где S_i – площадь i-ой части фигуры;

S – площадь всей фигуры.

Или центр тяжести однородного стержня:

, , , (7.4)

где l_i – длина i-ой части стержня;

l – длина всего стержня.

Замечание 1. Если однородное тело (фигура, стержень) имеет плоскость, ось или центр симметрии, то его цент тяжести расположен в плоскости симметрии, на оси симметрии или в центре симметрии.

Замечание 2. Если тело (фигура, стержень) имеет полости или вырезы, то при определении центра тяжести может быть использован способ отрицательных весов (площадей, длин). Способ заключается введение в числитель формул, кроме весов, площадей или длин без учета полостей или вырезов, и веса, площади или длин полостей или вырезов с отрицательным знаком.

7.2 Примеры решения задач

Задача 7.2.1

Определить равнодействующую и центр параллельных сил P и Q (рис. 7.2а), если модули сил равны P=15Н, Q=10Н, а расстояние между точками приложения сил AB=10м.

Рисунок 7.2

Решение.

Проведем оси Ox и Oy вдоль линии AB и перпендикулярно ей соответственно. Модуль равнодействующей параллельных сил определяем как сумму данных сил:

Центр параллельных сил (точки приложения равнодействующей) будет находиться на линии АВ. Координату точки определим формуле (7.1):

Откладываем от начала координат вдоль оси Ox 4 м (рис. 7.2б).

Ответ: R=25Н, xC=4м.

Задача 7.2.2

Определить равнодействующую и центр параллельных сил P и Q (рис. 7.3а), если силы направлены в противоположные стороны, их модули равны P=15Н, Q=10Н, а расстояние между точками приложения сил AB=10м.

Рисунок 7.3

Решение.

Аналогично с предыдущей задачей проводим оси координат и определяем модуль равнодействующей, учитывая направление сил:

.

Определяем положение центра параллельных сил, считая направление сил вдоль оси Oy положительным, а обратно - отрицательным:

.

Откладываем от начала координат вдоль оси Ox в отрицательном направлении 20 м (рис. 7.3б).

Ответ: R=5Н, xC=-20м.

Задача 7.2.3

Определить в координаты цента тяжести кронштейна, состоящего из однородных стержней AB=0,2м, BD=0,1м и DE=0,06 м, имеющих одинаковых линейный вес (рис. 7.4).

Рисунок 7.4

Решение.

Обозначим центы тяжести однородных стержней и найдем их координаты. Определим положение центра тяжести по формулам (7.4):

м,

м.

Обозначаем центр тяжести С на рисунке.

Ответ: x_C=0,0306м, y_C=-0,0606м.

Задача 7.2.4

Из однородной пластины в виде треугольника ОАВ с основанием ОВ=60см и высотой ОА=45 см вырезан полукруг радиуса r=20см (рис. 7.5). Определить в координаты центра тяжести полученной фигуры.

Рисунок 7.5

Решение.

Определяем площади фигур. Для треугольника ОАВ:

Для кругового сектора:

,

где α – угол сектора в радианах, α=π.

Координата центра тяжести треугольника находится на пересечении медиан. Эта точка делит каждую медиану в соотношении 2:1. Для нахождения центра тяжести прямоугольника достаточно от катетов отложить по 1/3 длины другого катета. Соответственно координаты центра тяжести треугольника ОАВ:

, .

Определяем координаты центра тяжести кругового сектора. Центр лежит на оси симметрии сектора, т.е. .

Ординату центра тяжести получим по формуле:

Определяем центр тяжести всей фигуры, учитывая, что вырезы берутся с отрицательным знаком:

,

.

Обозначим центр тяжести на рисунке.

Ответ: X_C=20 см, Y_C=20,676см.

Задача 7.2.5

Определить высоту H однородного прямоугольного параллелепипеда из условия, чтобы центр тяжести тела, состоящего из однородных пирамиды и параллелепипеда находился в плоскости ABCD (рис. 7.6). Высота призмы H₁=1,2м.

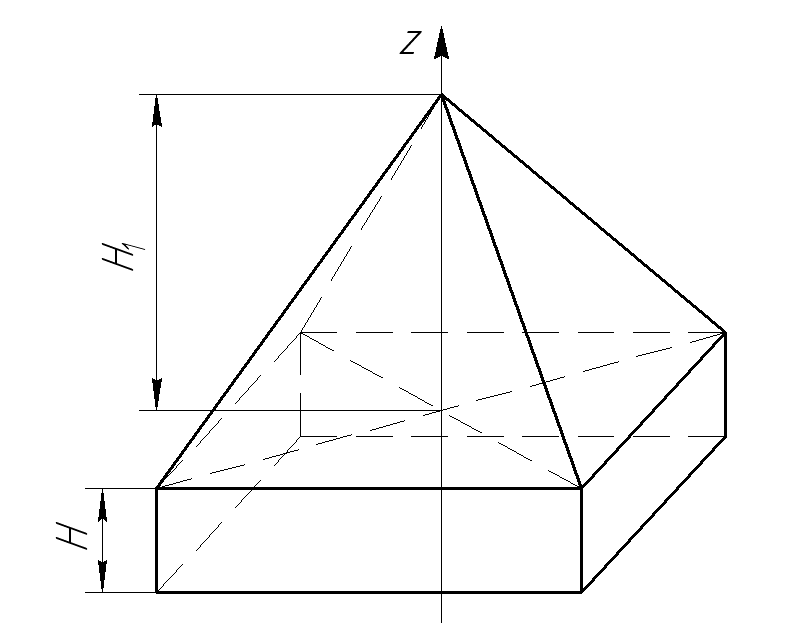
Рисунок 7.6

Решение.

Проведем ось z по оси пирамиды. За отметку «0» принимаем точку пересечения оси с основанием ABCD.

Объем пирамиды определяется как 1/3 произведения площади основания на высоту, а координата центра тяжести на расстоянии 1/4 высоты от основания, т.е. в нашем случае:

, .

Объем параллелепипеда и координата центра тяжести по оси Z:

, .

Центра тяжести тела должен иметь координату z=0:

Выражение равно нулю, если числитель равен нулю:

Ответ: H=0,49м