1.7.1.Розвязання np - повних задач.

Розрізняють дві загальні категорії підходів до розв”язання NP - повних задач. До першої категорії відносяться підходи, в яких робиться спроба скорочення об’єму перебору, хоча при цьому і визнається неминучість експоненціального часу роботи. Досить широко використовуються прийоми, засновані на методі “ гілок и границь” або методі “неявного перебору”. Їх сутність в побудові “часткових рішень”, представлених у вигляді дерева пошуку, та застосування потужних методів побудови оцінок, що дозволяють розпізнати безперспективні часткові розв’язку, в результаті чого від дерева пошуку відсікається ціла гілка за один шаг. До других підходів відносяться методи: динамічного програмування, методи відсічень та метод Лагранжа.

Підходи, які відносяться до другої категорії, застосовуються виключно до оптимізаційних задач і включають прийом, що називається “зниженням вимог”. Він полягає у відмовленні від оптимального розв’язку та в знаходженні “доброго” розв’язку за прийнятний час. Алгоритми, засновані на цьому прийомі, звично називають евристичними. Методи, які застосовують для побудови таких алгоритмів, досить сильно залежать від специфіки конкретних задач.

Хоча на практиці такі алгоритми виявляються досить задовільними, їх теоретична оцінка є доволі складною. Однак, в деяких випадках, вдається довести, що розв’язку, отримані евристичним алгоритмом, завжди будуть відрізнятися в процентному відношенні від оптимального розв’язку не більше, ніж на певну величину. Цей результат будемо розглядати як оцінку огріхи алгоритму.

Комбінаторна оптимізаційна задача П є або задачею мінімізації, або задачею максимізації і складається з 3 частин:

багатомножина D_п індивідуальних задач;

для кожної ІD_п кінцевої чисельності S_п(І) допустимих рішень індивідуальної задачі І;

функції т_п, що зіставляє кожній індивідуальній задачі ІD і кожному допустимому рішенню S_п(І) деяке додатне ціле число т_п(І, ), називається величиною розв’язку .

Якщо П - задача мінімізації (максимізації), то оптимальним розв’язкам індивідуальної задачі ІD_п є таке допустиме розв’язку *S_п(І), що для  S_п(І) виконана нерівність т_п(І,*) т_п(І,) (т_п(І,*) т_п(І,)). Для позначення оптимального розв’язку будемо використовувати ОРТ_п(І).

Алгоритм А називається наближеним алгоритмом розв’язку задачі П, якщо для  індивідуальні задачі ІD_п він шукає деяке допустиме розв’язку S_п(І). Величину т_п(І,) будемо позначати через А(І). Якщо А(І)=ОРТ(І) для  ІD_п то А називається точним алгоритмом.

Розглянемо задачу про “упаковку в контейнеры”.

Задана кінцева множина - “предметів” та “розміри” S(u)[0,1] для uU (раціональні числа).

Потрібно знайти таке розбиття чисельності U на неперетинні підчисельності U₁, ... , U_к, щоб сума розмірів предметів в  підчисельності U_і не перебільшувала І та щоб к було найменшим з можливих.

Алгоритм “в перший, який підходить”: Черговий предмет u: переноситься в контейнер з найменшим номером, в якого сума розмірів перенесеним предметів не перебільшує 1-S(u_i).

Позначимо функцію розв’язку цієї задачі FF(I), тоді (в результаті роботи алгоритму не може бути одного контейнера, заповненого наполовину).

Для оптимального розв’язку: ОРТ(І) ( ціла частина зі збільшенням)  для всіх індивідуальних задач FF(I)<2ОРТ(І), але можна краще.

Теорема. Для всіх індивідуальних задач І про “упаковку” має місце нерівність . (*є результат без 2*).

Більш того  індивідуальні задачі, для яких ОРТ(I) як завгодно велике та .

Тобто, величина FF(I) ніколи не відрізняється від оптимуму, більша ніж на 70% та в деяких випадках така відміна дійсно можлива.

Приклад. Індивідуальні задачі І з довільно великим значенням ОРТ(І), для яких FF(I) дорівнює 5/3 ОРТ(І).

ОРТ (І)=	1/2+Å	1/3+Å	1/7+Å	6т конт.
ОРТ (І)=	6т

т - контейнерів

1/7+Å6

1/3+Å

1/3+Å

3т - контейнерів FF(I)=10т

1/2+Å

6т - контейнерів

Незначне покращення алгоритму по правилу “в найкращий з підходящих” не є успішним. В найгіршому випадку цей алгоритм має по суті ті ж характеристики, що і алгоритм “в перший підходящий”.

Упорядкуємо предмети в порядку зменшення їх розмірів S(u₁) S(u₂) ...  S(u_n).Алгоритм будемо називати “в перший підходящий в порядку убування” - FFD(I).

Теорема. Для всіх індивідуальних задач про “упаковку” виконується нерівність .

Більш того, існують індивідуальні задачі І, для яких ОРТ(І) достатньо велике і .

Таким чином, ми маємо гарантію, що алгоритм навіть в найгіршому випадку відрізняється від оптимального не більш, чім на 22%.

Приклад. ОРТ(І)=9m

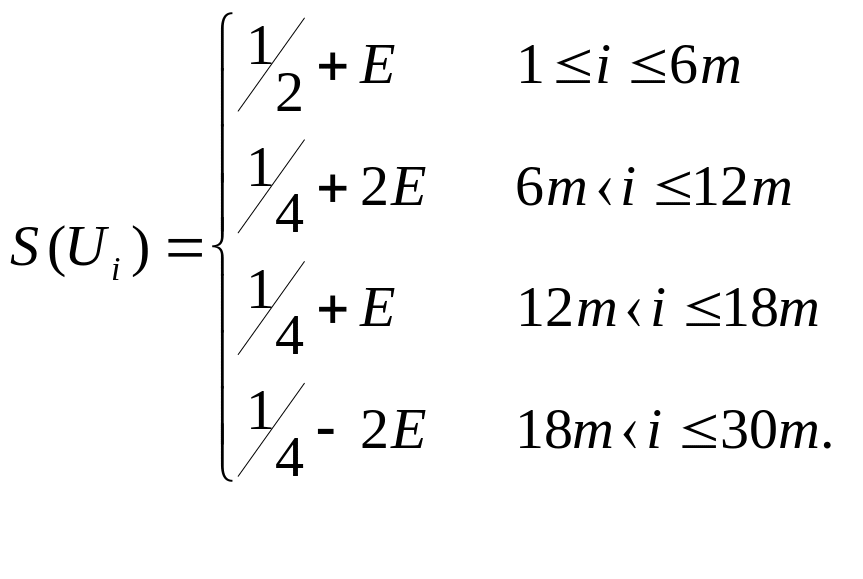
1/2+Å

1/4+Å

1/4-2Å

6т - контейнерів

1/4-2Å

1/4+2Å

1/4-2Å

1/4-2Å

3m - контейнерів

FFD(I)=11m.

1/2+Å

1/4+2Å

6m - контейнерів

1/4+Å

1/4+2Å

1/4+2Å

2m - контейнерів

1/4-2Å

1/4-2Å

1/4-2Å

1/4-2Å

3m - контейнерів

Для формалізації методики проектування наближених алгоритмів дамо ще декілька визначень.

Нехай П - задача мінімізації (максимізації), а І - довільна індивідуальна задача з Dп. Визначимо відношення R_A(I)=A(I)/OPТ(I) (або ОРТ(І)/A(I)).

Огріхою наближеного алгоритму А розв’язку задачі П назвемо величину R_A так, що

Асимптотичною погрішністю наближеного алгоритму А назвемо величину

Розглянемо задачу про комівояжера. Введемо допоміжні умови (“нерівність трикутника”). Потребуємо, щоб для кожної трійки місць a,b,c було виконано.

d(a, c)  d(a, b) + d(b, c).

При такому обмеженн³ задача залишаºться NP-важкою. Для ус³х алгоритм³в, як³ ми будемо розглядати в подальшому . Розглянемо алгоритм «найближчий сус³д» (NN), що полягаº у наступному:

в якост³ першого м³ста С_ï(1) в³зьмемо м³сто С₁;

якщо частковий маршрут побудовано, <C_Ï(1), Ñ_Ï(2), ..., Ñ_Ï(ê)> К<m вже побудовано, то в якост³ м³ста С_Ï(ê+1) вибираºмо м³сто С, найближче до м³ст С_Ï(ê).

Теорема Äëÿ ID_Ï - задач³ о ком³вояжер³, при виконанн³ нер³вност³ трикутника, з m-м³стами

NN(I)  ([log₂m] + 1)OPT(I)

Б³льш того, для пов³льно великих значень m ³снують так³ ³ндив³дуальн³ задач³ ² з m м³стами, що

NN(I)  (log₂(m+1) + )OPT(I)

З ц³º¿ теореми випливаº R_NN = .

Приклад

Оптимальний маршрут по периметру дорівнює 15, а NN(I) = 27. RNN(I) =  = (log2(m+1) + ) /* (4+ )= * = = = ; */ Демонстрація факту: вельми розумні евристики можуть приводити до поганих результатів, що відрізняються від оптимуму в довільно велику кількість разів.

Для цієї задачі існують алгоритми з огріхою R_A=2. Існує алгоритм, що заснований на понятті «мінімальне остовнее дерево». У повному графі відповідної здачі комівояжера  очевидна взаємо-однозначна відповідність між усякими можливими маршрутами і гамільтоновими циклами.

Означення. Остовним деревом називається зв’язний підграф, що містить усі вершини й не містить циклів ( він повинен мати m-1 ребро ). Мінімальним остовним деревом називається остовне дерево, сума довжин ребер котрого мінімальна.

Мінімальне остовне дерево можна побудувати поліноміальним алгоритмом. Довжина МОД для  графа менше довжини мінімального маршруту ( остовне дерево можна отримати відкиданням одного ребра ). Короткий маршрут можна побудувати по МОД в результаті подвійного обходу дерева.

В результаті такого підходу деякі міста доводиться відвідувати більше одного разу, однак отриманий маршрут можна скоротити, якщо кожний раз йти до ще невідвіданого міста.

З нерівності трикутника випливає, що довжина такого маршруту не збільшилась. Таким чином, довжина маршруту по алгоритму MST ( Minimum Spanning Tree ) не перевершує подвоєної довжини мінімального маршруту.

Теорема. Для усіх індивідуальних задач про комівояжера ІD_п , для котрих виконується нерівність трикутника, має місце нерівність:

MST(I)  2  OPT (I),

причому ця оцінка найкраща з можливих.

Позначимо алгоритм, побудований із застосуванням техніки паросполучення - ММ(І), тоді:

Теорема 2. ММ(І)  ОРТ(І).

В наш час алгоритмів з найкращою оцінкою не існує.

На жаль, мається велика кількість NP-важких задач, для котрих невідомі поліноміальні алгоритми, навіть з такою оцінкою похибки.

Наприклад – задача про розмалювання графа:

Задано граф G = ( V, E ). Потрібно знайти таку функцію f: V (1, 2, ..., k ), що f(u)  f(v), якщо u, v  E і k найменш можливе.

Найкраща з відомих в теперішній час оцінок похибки для поліноміальних алгоритмів А розв’язку задачі про розмалювання графа має вигляд

Іншими словами, для задачі про розмалювання графа не відомий поліноміальний наближений алгоритм з оцінкою похибки R_A 8. Такими ж, більш «складними» задачами являються задача комівояжера ( без нерівності  ), побудова максимальної за потужністю множини незалежних вершин в графі.

Необхідно відмітити, що підрозділ задач на задачі, що добре і погано розв’язуються наближеними методами не мають відношення до того факту, що задачі зв’язані поліноміальною зводимістю. Можна було б припускати, що така зводимість дозволяє перетворити добрий наближений алгоритм розв’язання однієї задачі в добрий наближений алгоритм розв’язання іншої.

Розглянемо задачі, що розв’язуються наближеними алгоритмами набагато краще. Повернемось до задачі про РЮКЗАК.

Задано кінцева множина U «предметів» для кожного з uU «розмір» S(a)I⁺ й вартість V(u) I⁺, а також додатне число BmaxS(u): uU – “ємність “ рюкзака. Потрібно знайти таку підмножину U’ U, що , і величина приймає максимальне значення.

Існує “жадібний алгоритм” (GA) - розвязання цієї задачі. Упорядкуємо множину U=u₁,u₂, ..., u_n за зменшенням “питомої цінності”, тобто т.ч. . Потім, починаючи з пустої множини U , послідовно додаємо до нього предмети зі списку, причому при додаванні предмету U_i перевіряємо, чи не перевищує сума розмірів, що вже містяться в U’ предметів, величини B – S(U_i). Такий алгоритм має похибку R_GA = 2.

Однак, Сахні показав, що для усіх K  1 існує такий наближений поліноміальний алгоритм А_к, що . Час роботи такого алгоритму поліноміально залежить від n, log V, log S, (де , ), але ці поліноми містять К в показнику степені.

Інший підхід, що дозволяє досягнути цієї ж точності більш швидким алгоритмом, базується на тому, що задача про рюкзак може бути розв’язана псевдополіноміальним оптимізаційним алгоритмом. Завдяки округленню та масштабуванню подібний алгоритм може бути перетворений в поліноміальний.

IA – псевдополіноміальний оптимізаційний алгоритм розв’язання задачі про рюкзак, часова складність якого

Кожну індивідуальну задачу про рюкзак можна модифікувати, замінюючи вартості усіх предметів для будь-якого фіксованого К>0. Для застосування алгоритму А_К задачі, що виникла потрібен час

.

Більш того, так як оптимальний розв’язок не може містити більш n предметів, то вартість оптимального розв’язку початкової задачі і модифікованої пов’язані наступним способом

OPT(I) – K  OPT(I’)  K_n

Відмітимо, що K  OPT(I’) не перебільшує вартості оптимального розв’язку задачі I’, що виражається в початковій вартості. Таким чином, якщо взяти оптимальний розв’язок U’ задачі I’ в якості наближеного розв’язку задачі І, то його вартість буде відрізнятись від вартості оптимального розв’язку задачі І не більш, ніж на K_n.

Воберемо К, що залежить від початкової задачі І. , де k-фіксоване додатнє ціле число. В результаті отримаємо наближений алгоритм, що має часову складність . Оскільки отримаємо

Означення Апроксимаційною схемою для оптимізаційної задачі назвемо алгоритм А для кожної індивідуальної задачі видає такий припустимий розв’язок , що .

Наближена схема А називається наближеною схемою з поліноміальним часом роботи, якщо для кожного алгоритм, що йому відповідає, має поліноміальну часову складність.

Для оптимізаційної задачі назвемо асимптотично найкращою досяжною відносною похибкою величину

Для розв’язку задачі існує такий наближений поліноміальний алгоритм A, r .

Можна припустити, що існують NP-складні задачі, для яких і існує т.ч. .

Розглянемо оцінку виду для усіх індивідуальних задач”І має місце оцінка , де К константа.

Теорема. Якщо P  NP, то не існує поліноміального наближеного алгоритму А для розв’язання задачі про рюкзак з оцінкою

де К – константа.

Доведення. Від противного. Нехай А – такий алгоритм, покажемо що його можна застосувати для точного розв’язку задачі. Задана індивідуальна задача І, побудуємо задачу І’, замінюючи вартість кожного предмету V(U) величиною (K+1)V(U). Припустимі розв’язки задачі І будуть такими ж, що й у задачі І, а величина розв’язку задачі І’ рівно в К + 1 разів більше величини розв’язку задачі І, що їй відповідає. Оскільки величина любого розв’язку задачі І – ціле кратне величини К+1, то із співвідношення виходить, що і, отже

що суперечить тому, що P  NP.

Те саме можна показати і для задачі про максимально незалежну множину. Взагалі, так як основна властивість, що використовується при доведенні, – множина припустимих розв’язків не змінюється, то доведення такого типу широко поширені.