1.4.Поліноміальна зведеність np-повної задачі

Якщо P не зпівпадає з NP, то розбіжності між P та NP\P значно суттєві. Всі задачі із P можуть бути розв'язані поліноміальними алгоритмами, а всі задачи NP\P важкорозв'язувані. Тому, якщо P  NP, то для кожної конкретної задачі П  NP важливо знати, яка із двух можливостей реалізується. До тих пір, поки не доведено, що P  NP, немає надії показати, що деяка конкретна задача належить NP\P. З цієї причини мета теорії складності полягає в доведенні більш слабких результатів виду: “якщо P  NP, то П  NP\P”.

Основна ідея подібного умовного підходу основана на перетворені задач та понять поліноміальної зведенності

Задача П₁ перетворюється в задачу П₂, якщо будь-яка індивідуальна задача І  П₁ перетворюється за поліноміальний час в деяку індивідуальну задачу J  П₂, т.щ. розв'язок задачі П₁ можна отримати за поліноміальний час з розв'язок задачі J  П₂. В цьому випадку будемо казати, що П₁ поліноміально зводиться до задачі П₂ і позначимо це як — П₁  П₂.

Вихід П₁

Вихід П₂

Вхід П₂

Вхід П₁

Алгоритм

для П₂

Алгоритм

для П₂

Перетвор.

за пол. час

Перетвор.

за пол. час

Р

Перетвор.

за пол. час

ис. 1.1. Схема поліноміального перетворення задачі П₁ в задачу П₂ [2]

Нехай П₁ та П₂ — задачі розпізнавання властивостей. Тоді поліноміальна зведенність задачі П₁ до задачі П₂ означає наявність функції : D_П1  D_П2, яка задовольняє двом умовам:

а) — обчислюється поліноміальним алгоритмом

б) для всіх D_П1 , Y_П1 тоді і тільки тоді, коли ( ) Y_П2 .

Щоб отримати конкретне уявлення про смисл цього визначення, розглянемо приклад.

Нехай — граф з множиною вершин та множиною ребер . Простим циклом в називаеться така послідовність < , , > різноманітних вершин із , що  ,  ,  < k , і  ,  Гальмітоновим циклом в називаеться простий цикл, який містить всі вершини графа

Задача гамільтонів цикл полягає в відповеді на питання — чи вірно, що граф . містить гамільтонів цикл.

Покажемо, що задача гамільтонів цикл (ГЦ), зводиться до задачі комівояжор (КМ). Для цього побудуемо функцію , яка відображає кожну індивідуальну задачу із ГЦ у відповідну індивідуальну задачу із КМ і задовольняє двом умовам поліноміальної зведенності.

Функція визначається наступним чином.

Нехай ,   = — фіксована індивідуальна задача із ГЦ. Відповідна задача із КМ будується так: множена графів C співпадає з ; для будь-яких двох міст , C відстань . між ними покладемо рівною 1, якщо  ,  , i 2 в іншому випадку. Межа для довжини шуканого маршруту береться рівною .

Легко помітити, що функція здійснює зведеність і може бути обчислена за поліноміальний час. Для перевірки другої вимоги необхідно показати, що містить гамільтонів цикл тоді і тільки тоді, коли в є маршрут який проходить через всі міста і не перевищує .

Нехай < , ,…, > — гамільтонів цикл тоді < , ,…, > маршрут в , а його довжина рівна ( = ). Так як відстань між будь-якими сусідніми містами маршрута рівна 1. Навпаки, нехай < , ,…, >. — маршрут в , довжина якого не перевишує Оскільки відстань між мистами рівна або 1, або 2 і при обчислені довжини маршрута сумується рівно відстаней, то із того, що = випливає, що відстань між парою сусідніх міст в маршруті рівна 1. По визначенню випливає що  ,  1  <  , — є ребрами графа , і, от же, < , ,…, > — гамільтонів цикл в Таким чином ГЦ  КМ.

Задача розпізнавання П називається NP-повною, якщо П  NP і будь-яка інша задача розпізнавання П  NP зодиться до П. Таким чином NP-повні задачі ніби “найважчі задачі із NP”. Якщо хочаб одна NP повна задача може бути розв'язана за поліноміальний час, то і всі задачі із NP також можуть бути розв'язані за поліноміальний час. Отже, будь-яка NP-повна задача П володіє властивістю: П  P. тоді і тільки тоді, коли P = NP.

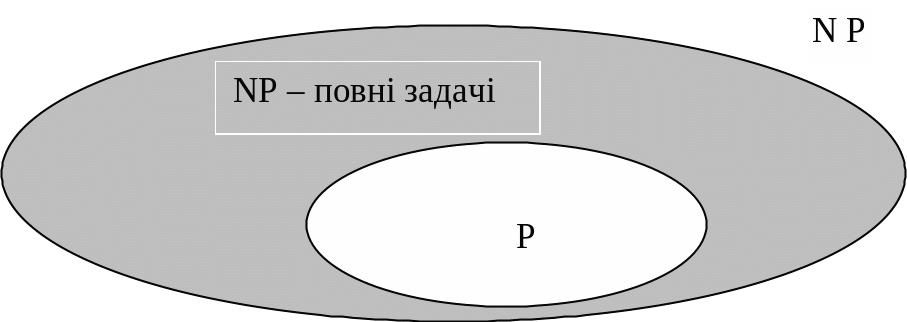
Рис. 1.2. Співідношення между класами P i NP задач