Уравнение токов транзистора.

Для вывода уравнений токов транзистора заменим его идеализи­рованной эквивалентной схемой, показанной на рис.4.8.

Модель транзистора, представленная на рис.4.8, получила название модели Молла-Эберса.

В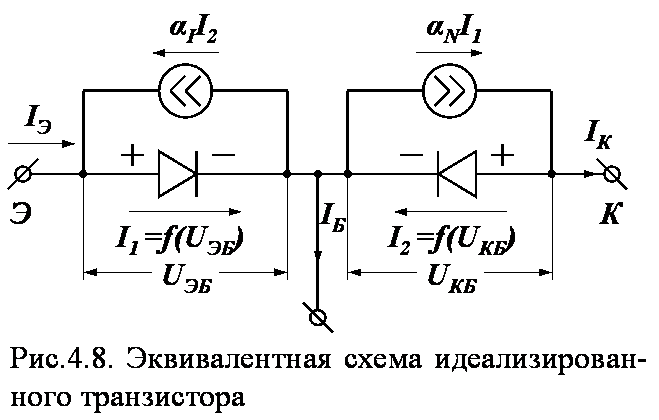 этой схеме не учитываются объемные сопротивления эмиттерной и коллекторной областей (их влияние несущественно), а также с целью упрощения анализа, не учитывается сопротивление базы. В дальнейшем сопротив­ление базовой области будет учтено особо. Кроме того, при выводе уравнений токов транзистора не учитывается эффект модуляции ширины базы.

Каждый из p-n пере­ходов транзистора представ­лен на эквивалентной схеме в виде диода, а взаимодейст­вие переходов отражено генераторами тока, включенными параллельно соответствующим диодам. Из эквивалентной схемы следует, что

, (4.10)

. (4.11)

Как видно, в общем случае токи и складываются из двух составляющих: инжектируемой ( или ) и собираемой ( или ). Величины и представляют собой коэффици­енты передачи тока для нормального или обычного - и инверсно­го - включения транзистора (в инверсном включении эмиттер выполняет функцию коллектора, а коллектор - эмиттера).

Токи или зависят от напряжений так же, как в обычном диоде:

, (4.12)

(4.I3)

В эти выражения входят и - тепловые токи эмиттерного и коллекторного диодов, измеряемые соответственно при .и . Их можно легко выразить через токи и , проте­кающие в цепи эмиттер - база или коллектор - база в режиме холосто­го хода, либо коллекторной ( ), либо эмиттерной ( ) цепи. Например, полагая , из (4.10) получаем . Из (4.13) при следует, что . С учетом этого из (4.12) имеем . Следовательно,

(4.14)

Аналогично можно получить

(4.15)

Подставляя (4.12) и (4.13) соответственно в (4.10) и (4.11), получаем:

; (4.16)

. (4.17)

Так как , то, с учетом (4.16) и (4.17), будем иметь:

(4.18)

Формулы (4.16)-(4.18) получили название формул Молла-Эберса. Несмотря на свою приближенность, они достаточно хорошо отражают основные особенности работы транзисторов при любых сочетаниях напряжений и .

Ниже проводится анализ статических характеристик транзистора для трех схем включения, показанных на рис.4.9.

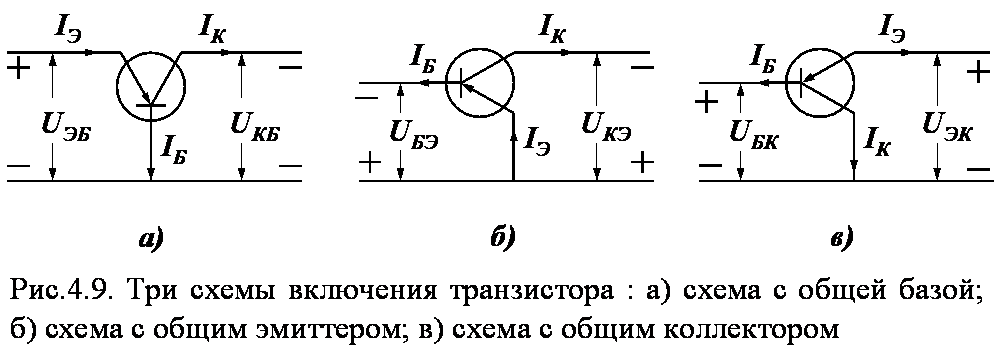
Статические характеристики выражают функциональную связь между постоянными токами и напряжениями транзистора. Заметим, что физические процессы в транзисторе не зависят от схемы включения. Вид статических характеристик определяется выбором независимых переменных.

Статические характеристики тран­зистора, включенного по схеме с общей базой.

В схеме с общей базой используются следующие семейства характеристик:

, при - входные характеристики;

, при - характеристики передачи по току;

, при - выходные характеристики;

, при - характеристики обратной связи по напряжению.

Из этих четырех семейств наибольшее применение на практике находят входные выходные характеристики транзистора.

Идеализированные статические характеристики.

Входные характеристики идеализирован­ного транзистора определяются зависимостью (4.16). Если, учесть (4.14) и (4.15), то будем иметь следующее выражение для входных характеристик:

. (4.19)

Выразив из (4.16) двучлен и подставив его в (4.17), получим выражение для выходных характеристик транзистора

. (4.20)

Семейства входных и выходных характеристик, построенные в соответствии с (4.19) и (4.20), показаны на рис.4.10.

Относительно семейства входных характеристик можно заметить следующее. Характеристика, соответствующая , является характеристикой обычного p-n перехода. При положительных нап­ряжениях на коллекторе кривые сдвигаются вправо и вниз. Это объясняется нарастанием собираемой компоненты эмиттерного тока (второй член в выражении 4.19). При отрицательных напряже­ниях на коллекторе кривые незначительно смещаются вле­во и вверх.

Если , то влияние изменения коллекторного напряже­ния практически отсутствует.

Выходные характеристики представлены на рис.4.10,б. Для удобства обратное напряжение на коллекторе (отрицательное для транзистора p-n-p и положительное дня транзистора n-p-n) принято откладывать вправо. При изменении тока эмиттера на одинако­вую величину характеристики оказываются эквидистантными, так как коэффициент передачи тока эмимера предполагается постоянным. На рис.4.10,б можно видеть различные режимы работы транзистора: активный режим, соответствующий напряжению (первый квадрант), режим насыщения, соответствующий напря­жению (второй квадрант) и режим отсечки, границей которо­го является кривая .

Для активного режима работы выполняются условия и . Поэтому формулы (4.19) и (4.20) упрощаются:

(4.21)

(4.22)

При выводе (4.21) использовано выполняющееся в транзисторах соот­ношение и для простоты положено . Заметим, что из (4.22) следует независимость тока от напряжения , т.е. кривые параллельны оси напряжений.