Применение обобщенного метода оценивания параметров моделей на практике (некоторые случаи).
А) Эконометрические модели с коррелирующими ошибками
При наличии автокорреляционных взаимосвязей в ряду ошибки ковариационная матрица формально может быть представлена в виде:
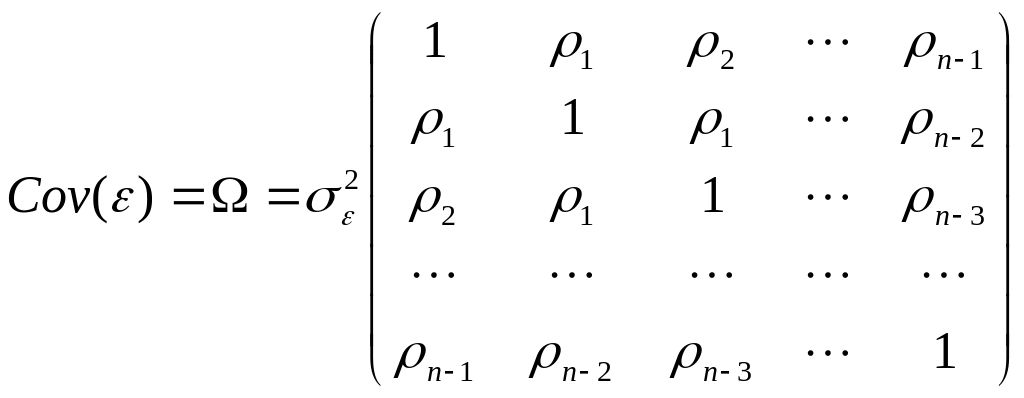
Можно
воспользоваться следующим практическим
подходом
к оценке недиагональной ковариационной
матрицы
ошибок эконометрической модели,
отражающей существование корреляционной
зависимости между ее значениями. Этот
подход не требует предварительной
информации относительно характера
взаимосвязей между ее последовательными
значениями
.
Согласно этому подходу матрица Cov(e)
рассматривается как оценка ковариационной
матрицы истинной ошибки модели
Cov(ε),
находится эмпирическим путем в несколько
этапов:
1)
на основании исходных данных – вектора
у
и матрицы Х
– формируется уравнение эконометрической
модели, затем с помощью МНК оцениваются
ее параметры, определяется вектор
фактической ошибки е,
значения которого проверяют с помощью
критериев (например, Дарбина – Уотсона)
на наличие автокорреляции. В том случае,
если факт корреляции установлен, то на
основе эмпирического ряда ошибки
оцениваются элементы ее ковариационной
матрицы по формуле
,
k=1,
2,…
2)
определенную таким образом ковариационную
матрицу фактической ошибки
используют для оценки параметров той
же модели с помощью ОМНК (формула (4)).
Далее вычисляется новый ряд фактической
ошибки, происходит проверка на наличие
автокорреляции и, в случае подтверждения
этой гипотезы, определяется новая
матрица
.
Затем с помощью ОМНК вычисляется третий
вариант оценок параметров.
Процедура построения модели завершается, если критерий Дарбина – Уотсона не подтверждает наличие автокорреляции в ряду ошибок очередного этапа оценивания модели. На практике чаще всего достаточно произвести одну итерацию.
Б) Эконометрические модели с гетероскедастичными ошибками
В случае гетероскедастичности ошибок ковариационная матрица имеет вид:
Для
эконометрических моделей с
гетероскедастичными ошибками может
быть применена процедура последовательных
этапов расчетов, как и в случае
автокорреляции между ошибками модели.
Для этого на первом этапе по результатам
применения обыкновенного МНК должны
быть сформированы оценки
матрицы Cov(e).
Сделать это на основе значений фактической
ошибки
для каждой точки t
= 1, 2,…, n
невозможно. Вследствие этого приходится
привлекать некоторые дополнительные
гипотезы относительно характера
изменения дисперсии ошибки, например,
гипотезу о линейном законе ее изменения.
При
таком предположении оценки дисперсий
могут быть определены следующим образом.
Для двух непересекающихся интервалов
и
по значениям фактических ошибок
и
могут быть получены оценки дисперсий
и
,
которые соотносятся с моментами t
= l
и
t
= m,
являющимися серединами этих рядов.
Далее на основе этих двух значений
строится линейная зависимость
,
аппроксимирующая изменение дисперсии
на интервале (1,
T).
Каждое из найденных значений
будет представлять собой оценку
соответствующего элемента диагональной
матрицы Ω.
Эта матрица затем используется на втором
этапе вычислений оценок параметров
модели при помощи ОМНК.
Подобная процедура может быть реализована при любых правдоподобных гипотезах о закономерности изменения дисперсии ошибок, например, для квадратичной закономерности, для логарифмической зависимости и т.д.