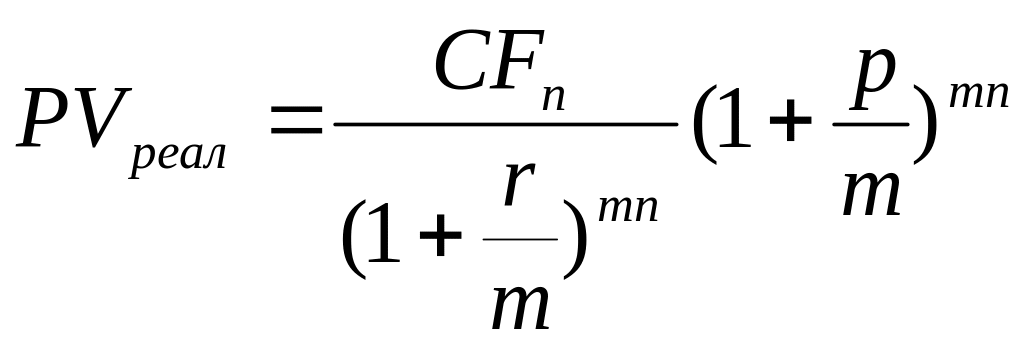11. Учет инфляции в финансовых расчетах

Инфляционные процессы, характерные для экономики многих стран, требуют того, чтобы они учитывались в финансовых расчётах. Особенно необходимо рассчитывать воздействие инфляции при вычислении наращенных сумм и определении действительной ставки процентов.

Внешними признаками инфляции являются, прежде всего, рост цен, и как следствие, снижение покупательной способности денег. Если индекс цен обозначим I_p, а покупательную способность денег через I_D, то I_D=1/I_p. Индекс покупательной способности денег есть величина, обратная индексу цен. Отсюда следует, что отношение наращенной суммы денег к индексу цен S/I_p характеризует реальную покупательную способность наращенной суммы.

Допустим, что в течение двух лет цены в среднем растут ежегодно на 58,11% (I_p=1,5811), тогда за два года они вырастут в 2,5 раза, так как (1+0,5811)²=2,5. Если первоначальная сумма P=2 млн. р. была помещена в банк под 120% годовых (сложные проценты) на 2 года, то по истечении этого срока наращена сумма составит S=2*(1+1,2)²=9?68 млн. р. Однако с учётом инфляции S_инфл=9,68/2,5=3,872 млн. р. Если принять 3,872 млн. р. за фактически наращенную сумму, то реальная доходность составит i=(S/P)^1/n-1=0.3914 (39,14%).

Так как темп прироста цен α в основном соответствует темпу прироста инфляции, то годовой индекс цен составит велинину α. За n лет индекс (1+α)ⁿ. Поэтому наращенная сумма за срок n лет, с учётом обесценивания составит: S_инфл=P(1+i)ⁿ/(1+α)ⁿ=P*[(1+i)/(1+α)]ⁿ. Величина множителя наращения [(1+i)/(1+α)]ⁿ зависит от изменения банковской стаки и темпа прироста инфляции. Если темп прироста инфляции равен ставке начисляемых процентов, то покупательная способность наращенной суммы будет равна покупательной способности денег. Если же α>I, то полученная наращенная сумма не компенсирует инфляции.

Уравнение Фишера — уравнение, описывающее связь между темпом инфляции, номинальной и реальной ставками процента:

i_a=i_r+a для значений которые меньше 10%,

либо более точная: i_a=i_r+a+i_r*a, где

i_a — номинальная ставка процента;

i_r — реальная ставка процента;

a — темп инфляции.

Уравнение показывает, что номинальная ставка процента может измениться по двум причинам:

из-за изменений реальной ставки процента;из-за темпа инфляции.

Например, если субъект положил на банковский счёт сумму денег, приносящую 10 % годовых ежегодно, то номинальная ставка составит 10 %. При уровне инфляции 6 % реальная ставка составит только 4 %.

Наращение по простым процентам (n>1) с учетом инфляции
Наращение по сложным процентам с учетом инфляции
Наращение по номинальной процентной ставке с учетом инфляции
Дисконтирование по простым процентам (n>1) с учетом инфляции
Дисконтирование по сложным процентам с учетом инфляции
Дисконтирование по номинальной процентной ставке с учетом инфляции
Коммерческий учет по простым процентам с учетом инфляции
Коммерческий учет по сложным процентам с учетом инфляции
где PV (Present Value)	текущая стоимость
FV (Future Value)	будущая стоимость
CFt (Cash Flow)	денежный поток в период t
n	число процентных периодов или интервал начисления
r (Rate of interest)	процентная ставка
d	учетная ставка
m	число начислений в году
p	уровень инфляции, выраженный в долях единицы