
- •Пояснювальна записка
- •Перелік лабораторних робіт включених у збірник
- •Лабораторна робота №1 тема: виконання операцій додавання та віднімання чисел з фіксованою та плаваючою комою
- •1. Мета роботи
- •2.Основні теоретичні відомості Форми представлення чисел в комп’ютерах
- •Кодування чисел та знаків в комп’ютерах
- •Алгоритми виконання операцій додавання і віднімання двійкових чисел
- •3. Домащнє завдання.
- •4. Виконання роботи.
- •5. Контрольні запитання.
- •Лабораторна робота №2 тема: виконання операцій множення та ділення чисел з фіксованою та плаваючою комою
- •1. Мета роботи
- •2.Основні теоретичні відомості Множення чисел, представлених у формі з плаваючою комою
- •Ділення чисел, представлених в формі з плаваючою комою
- •3. Домашнє завдання.
- •4. Виконання роботи.
- •5. Контрольні запитання.
- •Лабораторна робота №3 тема: мінімізація функцій алгебри логіки
- •1. Мета роботи
- •2.Основні теоретичні відомості
- •Мінімізація методом Квайна.
- •Мінімізація функцій Буля за допомогою карт Карно (табличний метод).
- •3. Домашнє завдання.
- •4. Виконання роботи.
- •5. Контрольні запитання.
- •Лабораторна робота №4 тема: синтез логічних схем та їх дослідження на лабораторному макеті
- •1. Мета роботи
- •2.Основні теоретичні відомості
- •Етапи синтезу кцп в базисі і, або, не.
- •3. Домашнє завдання.
- •4. Виконання роботи.
- •5. Контрольні запитання.
- •Лабораторна робота №5 тема: дослідження роботи дешифратора
- •1. Мета роботи
- •2.Основні теоретичні відомості
- •3. Домашнє завдання
- •4. Виконання роботи
- •5. Контрольні запитання.
- •Лабораторна робота №6 тема: дослідження перетворювача прямого коду в додатковий
- •1. Мета роботи
- •2.Основні теоретичні відомості
- •3. Домашнє завдання
- •4. Виконання роботи
- •5. Контрольні запитання.
- •1. Мета роботи
- •2.Основні теоретичні відомості
- •3. Домашнє завдання
- •4. Виконання роботи
- •5. Контрольні запитання.
- •Лабораторна робота №10 тема: дослідження лічильників з різними коефіцієнтами ліку
- •1. Мета роботи
- •2.Основні теоретичні відомості
- •3. Домашнє завдання
- •4. Виконання роботи
- •5. Контрольні запитання.
- •Рекомендована література
Мінімізація методом Квайна.
Мінімізацію по Квайну потрібно починати із ДДНФ функції. Якщо функція задається в довільній формі, то її необхідно перетворити до ДДНФ.
Для цього член в записі функції, який не містить якого-небудь аргумента, множимо на логічну одиницю , і таким чином одержуємо два члена, які містять весь набір аргументів, а потім до функції застосовуємо операції склеювання і поглинання, щоб одержати скорочену ДНФ функцію.
Розглянемо
етапи мінімізації логічної функції
![]() ,
заданій в ДДНФ.
,
заданій в ДДНФ.
В даній функції
- об'єднуємо елементарні добути, отримаємо
-
![]() ,
маємо
,
маємо
![]() .
.
У результаті застосування правила склеювання у виразі логічної функції зменшується число підсумовуваних добутків і число змінних.
Таким чином, мінімізація функцій Буля проводиться за допомогою законів і теорем алгебри логіки, теореми де Моргана, закона подвійного заперечення і правил поглинання і склеювання.
Мінімізація функцій Буля за допомогою карт Карно (табличний метод).
Карта Карно — це прямокутник, розбитий на квадрати (комірки), число яких дорівнює 2n , де n- число логічних змінних. Структура карт Карно для 2-х, 3-х, 4-х змінних показана на рис. 3.1.
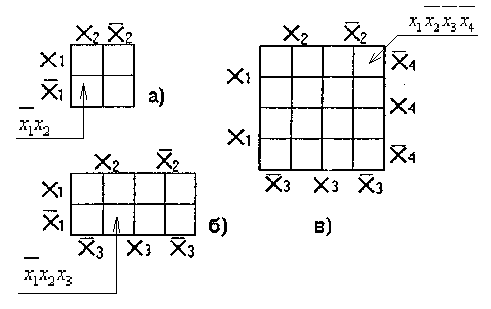
Рис.3.1. Карти Карно: а) для функції 2-х аргументів;
б) для функції 3-х аргументів;
в) для функції 4-х аргументів;
Комірки карти відповідають значенням вхідних змінних. Наприклад, верхній рядок карти для функції 3-х змінних відповідає "1", тобто значення х1=1, а нижній рядок - нульовому значенню х1=0 кожний стовпчик характеризується значенням двух змінних х2 і х3.
Для табличної заданої функції у комірки карта Карно проставляють значення функції для відповідних наборів аргументів, рис.2.
Пошуки мінімальної форми функції зводяться до визначення областей, які містять по 2k комірок, де 2- число, k-ціле число (0, 1, 2...). В області об'єднуються сусідні комірки, які відповідають сусіднім елементарним добуткам рис.3.
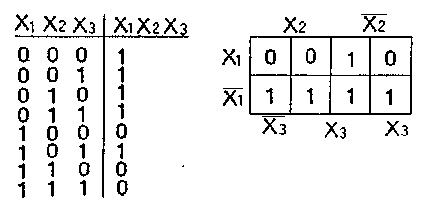
Рис. 3.1
Такій
мінімізації відповідає вираз:
![]() .
Карти Карно можна уявно звертати,
що дасть змогу побачити найбільш короткі
імплеканти результуючі кон'юнкції,
рис.3.2.
.
Карти Карно можна уявно звертати,
що дасть змогу побачити найбільш короткі
імплеканти результуючі кон'юнкції,
рис.3.2.
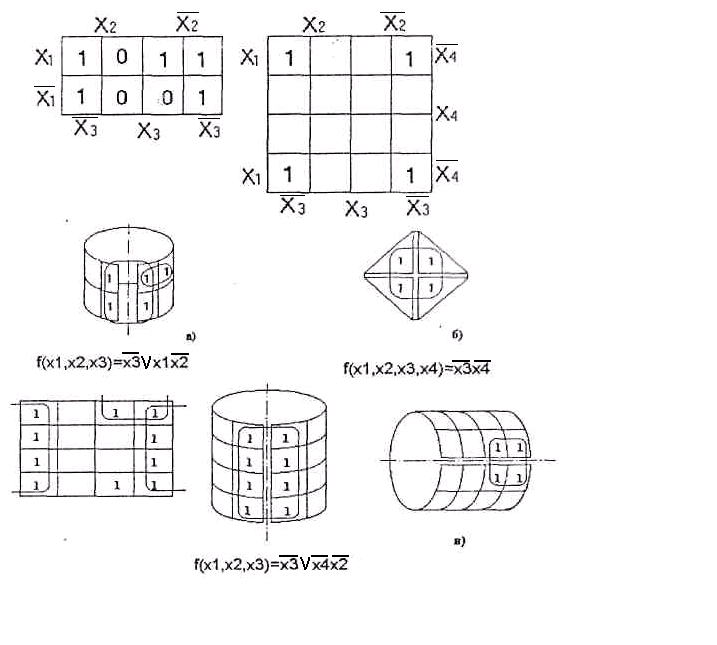
Рис. 3.2. Карти Карно і мінімальний запис логічних функцій:
а) для 3-х змінних; б),в) для 4-х змінних
Аналізуючи карти Карно, рис. 3, бачимо, що одна і таж комірка (наприклад, комірка з координатами х2х3) може покриватися два або декілька разів. Таким чином, формула, одержана в результаті мінімізації логічної функції за допомогою карт Карно, містить суму стількох елементарних добутків, скільки областей є в карті. Чим більше комірок в області, тим меньше змінних міститься у відповідному йому симентарному добутку.
3. Домашнє завдання.
3.1. Вивчити за опорним конспектом способи мінімізації логічних функцій.
3.2.Довести
тотожність, відмічаючи закон і правила
алгебри логіки застосовувані на кожному
кроці перетворення:
![]() .
.
3.3. Логічна функція задана картою Карно. Вибрати правильну відповідь, що відповідатиме мінімізованій формі. На карті Карно проставити відповідні змінні та виділити відповідні області при мінімізації. .
А)
|
1.
2.
3.
4.
5.
|
Б)
|
1.
2.
3.
4.
5.
|
