Етапи синтезу кцп в базисі і, або, не.

Задача 1. Потрібно сконструювати пристрій на виході якого високий рівень напруги з'явиться тільки в тому випадку, якщо високий рівень напруги поступає на вхід X₁ і на будь-який другий вхід (Х₂ або Х₃). Складемо таблицю істинності роботи пристрою, табл.4.1.

Таблиця 4.1

х1	х2	х3	f(x1x2x3)
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 0 0 1 1 1

Звернемо увагу, що три комбінації х₁, х₂, х₃ дають на виході логічну 1. Алгебраїчний вираз для функції і f(х₁,х₂,х₃) в ДДНФ має вигляд . Із даного виразу видно, що при проектуванні пристрою потрібно використати два інвертора (НЕ), три - 3-х елемента кон'юнкції (І) - логічне множення та одного елементу диз'юнкції (АБО - логічне додавання).

Використовуючи ці елементи будуємо цифровий пристрій, який зображено на рис. 4.1.

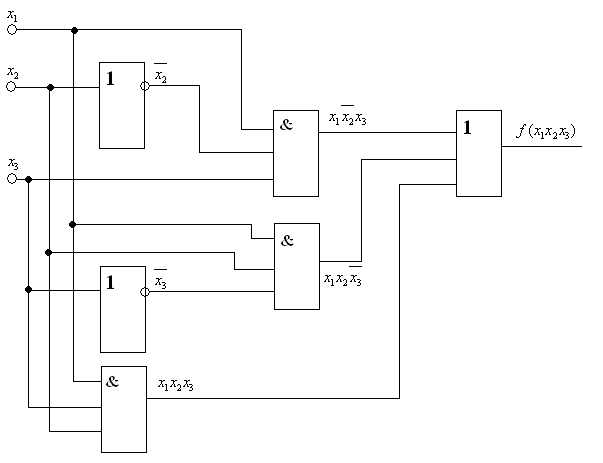
Рис.4.1

Як видно із логічного виразу структурна схема пристрою рис.4.1 не є оптимальною з точки зору числа логічних елементів і не є єдино-можливою схемою логічного пристрою, забезпечуючи обробку інформації відповідно з приведеною таблицею істинності (табл.4.1). Тому одним із важливих етапів є мінімізація логічного виразу, що зв'язано з використанням основних відношень законів та теореми алгебри логіки (метод Квайна).

Наприклад:

Якщо кількість змінних (х<6) тобто не велика, то вірні результати мінімізації дає метод з використанням карт Карно. рис.4.2.

Заповнимо карту Карно по таблиці 4.1.

Рис. 4.2

fМДНФ(х1х2х3)= х1х2۷ х1х3; fМКНФ(х1х2х3)= х1(х2۷х3);

Об'єднуємо одиниці в області (в область об'єднуються по 1,2,4,8 одиниць, або нулів), наступним етапом являється одержання мінімізованої диз'юнктивно-нормальної форми (МДНФ) логічної функції, або мінімізованої кон'юнктивно- нормальної форми (МКНФ) логічної функції. Таким чином для пред'явлених областей карт Карно МДНФ заданої функції має вигляд , яка співпадає з одержаною алгебраїчним методом мінімізованою формою. Логічний пристрій побудований по одержаному логічному виразу одержується більш простим, рис.4.3.

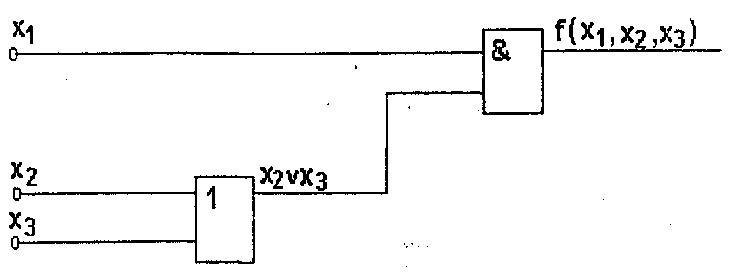
Рис. 4.3

В більшості випадків конструювання логічних схем починається з складання таблиці істинності, в якій для деяких заперечених наборів змінних .функція виходу недовизначена, тому необхідно уміти перетворювати інформацію в формі таблиці істинності в булевий алгебраїчний вираз. Невизначеність функції означає, що заперечені набори ніколи не з'являються в процесі роботи пристрою. Значить таку функцію можна до визначити, встановивши її значення (0 або 1) на заперечених наборах і це не впливає негативно на роботу пристрою, та полегшить його реалізацію

Задача 2. Побудувати пристрій, робота якого задана таблицею істинності, рис.4.4.

Рис.4.4

Рис.4.5

В клітках карт Карно, що відповідних запереченим набором, замінимо ті, які полегшать об'єднання одиниць, логічними 1, рис.4.5.

Якщо по карті Карно, рис.4 мінімізувати області, які задані тільки одиницями, то функція має вигляд , якщо ж до визначеної функції по карті Карно на рис.4.5 то її значення прийме вигляд: . Функція значення якої співпадає з значенням заданої функції на цих наборах називається еквівалентною.

Таким чином наша задача зводиться до відшукування такої еквівалентної функції, яка має простішу форму, а значить і пристрій буде біліш простішим, рис6

Рис.4.6

Для синтезу логічних пристроїв в базисі І-НЕ /АБО-НЕ/ необхідно виконати перетворення логічних виразів, заданих у МДНФ або МКНФ

МДНФ - мінімальна диз'юнктована нормальна форма;

МКНФ - мінімальна кон'юнктована нормальна форма.

В основу перетворення логічних виразів покладені:

• закон подвійного заперечення;

• формули де Моргана.

Нехай, наприклад, логічний вираз заданий в МДНФ:

Для переходу до базису І-НЕ виконуємо наступні дії:

• по закону подвійного заперечення ;

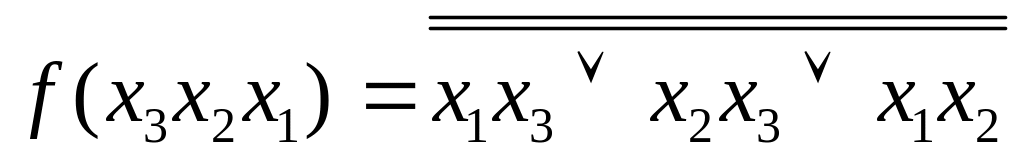• по формулі де Моргана

Для переходу до базису АБО-НЕ виконуємо наступні дії:

• по закону подвійного заперечення ;

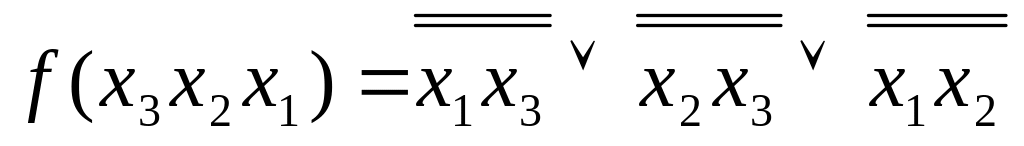• по формулі де Моргана .

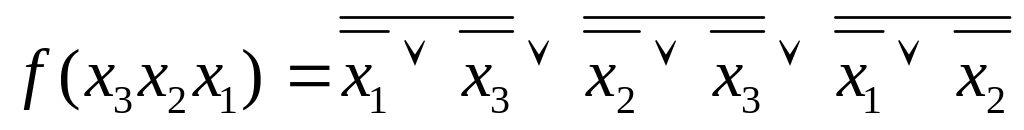• по закону подвійного заперечення .

Нехай, наприклад, логічний вираз заданий в МКНФ:

.

Для переходу до базису І-НЕ виконуємо наступні дії:

• по закону подвійного заперечення ;

• по формулі де Моргана ;

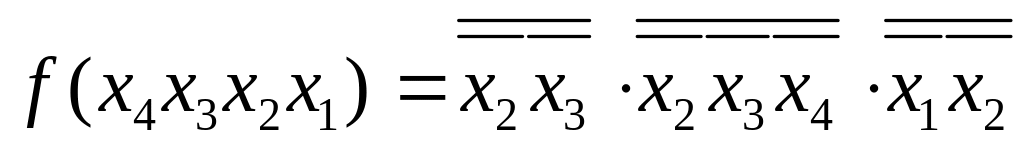• по закону подвійного заперечення .

Для переходу до базису АБО-НЕ виконуємо наступні дії:

• по закону подвійного заперечення ;

• по формулі де Моргана

При виборі заданих серій мікросхем для синтезу логічних пристроїв може виявитись, що число входів вибраних мікросхем більше чи менше потрібних по запису логічних виразів.

Наприклад, для синтезу логічних пристроїв по виразу підібрана мікросхема КР1533 ЛА4.

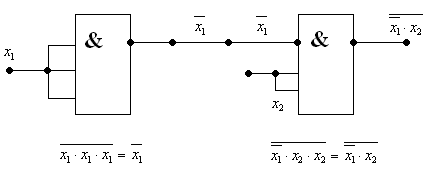
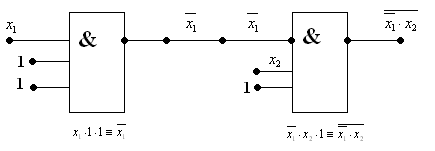
А)	Б)
Рис.4.7. Логічний пристрій на мікросхемі КР1533ЛА4

Нехай, наприклад, для синтезу логічного пристрою по виразу підібрана мікросхема КР1554 ЛЕ10, рис.4.8

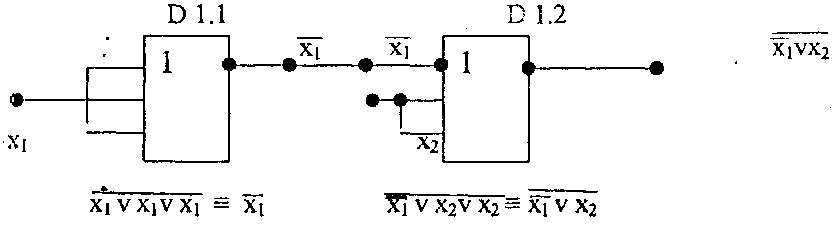
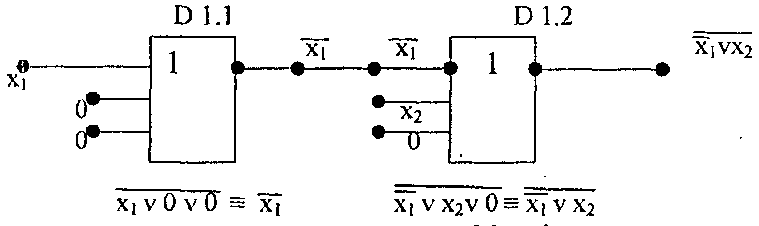
А)	Б)
Рис.4.8. Логічний пристрій на мікросхемі КР1554 ЛЕ10

Вхід мікросхем, який не використовується, залишати вільним небажано, із за впливу завад, які наводиться на цей вхід.

Спосіб об'єднання входів /Рис.7А, Рис.8А/ викликає збільшення навантаження для джерела вхідного сигналу, що приводить до зниження швидкодії за рахунок збільшення затримки розповсюдження сигналу. Спосіб подачі пасивних логічних рівнів на вхідних мікросхем, які не використовуються / Рис.7Б, Рис.8Б/ найбільш доцільний для практичного застосування.

Розглянемо випадок побудови логічних пристроїв на мікросхемах з недостатнім числом входів.

Наприклад, вибрана мікросхема КР1533 ЛАЗ для синтезу логічного пристрою по виразу: , рис.4.9.

Рис.4.9. Логічний пристрій на мікросхемі КР1533 ЛА3

Як видно із схеми Рис.4.9, синтез логічних пристроїв на мікросхемах зі зменшеним числом входів, потребує застосування більшого числа мікросхем.