Вопросы для самопроверки

1. Чем обусловлена необходимость применения моделей и моделирования?

2. Дайте определение модели, моделирования и теории моделирования.

3. Какие из известных методов моделирования наиболее широко используются при моделировании электроприводов?

4. Какое моделирование называют физическим?

5. Какое моделирование называют натурным?

6. Какое моделирование называют математическим и что является результатом математического моделирования?

7. Что такое иммитационное моделирование?

8. Назовите пакеты программ, с помощью которых наиболее эффективно может быть осуществлено моделирование электроприводов.

Р А З Д Е Л X

МОДЕЛИРОВАНИЕ РАЗОМКНУТЫХ ЭЛЕКТРОПРИ-ВОДОВ С ТРЕХФАЗНЫМ АСИНХРОННЫМ ДВИГАТЕЛЕМ

1. Математическая модель трехфазного асинхрон- ного двигателя с короткозамкнутым ротором в фазных осях

2. Виртуальная модель трехфазного асинхронного двигателя в MatLab 6.1

3. Результаты компьютерного моделирования пе- реходных и установившихся процессов в трех- фазном асинхронном двигателе с коротко- замкнутым ротором при питании от трех- фазного симметричного источника

4. Виртуальная модель трехфазного мостового автономного инвертора напряжения с широтно-импульсной модуляцией в MatLab 6.1

5. Результаты компьютерного моделирования переходных и установившихся процессов в трехфазном асинхронном двигателе с коротко- замкнутым ротором при питании от трех- фазного мостового автономного инвертора с широтно-импульсной модуляцией

1. Математическая модель трехфазного асинхронного двигателя с короткозамкнутым ротором в фазных осях

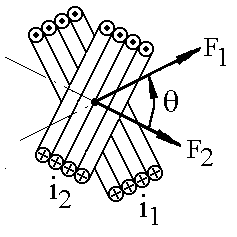
На рис. 66 показано пространственное расположение обмоток трехфазной идеализированной асинхронной электрической машины. На статоре имеются три обмотки с числом витков , на роторе - три обмотки с числом витков .

С осями обмоток совмещены координатные оси А, В, С статора и a, b, с ротора [7].

Рис. 66.

Здесь и далее условимся, что индексы указывают на принадлежность параметра соответствующей фазе статора; а индексы - на принадлежность параметра фазе ротора.

Система координат ротора перемещается относительно системы координат статора, их взаимное расположение характеризуется электрическим углом между осями.

Эти оси в теории электрических машин получили название естественных, или фазных, непреобразованных координат.

Исходная система дифференциальных уравнений трехфазного АД может быть записана в матричной форме на основании второго закона Кирхгофа с учетом уравнения Максвелла:

, (10.1)

где - матрица напряжений; - матрица активных сопротивлений; - матрица токов; - матрица потокосцеплений; - матрица индуктивностей.

Матрицы трехфазного АД, входящие в (10.1), имеют следующий вид:

; (10.2)

; (10.3)

; (10.4)

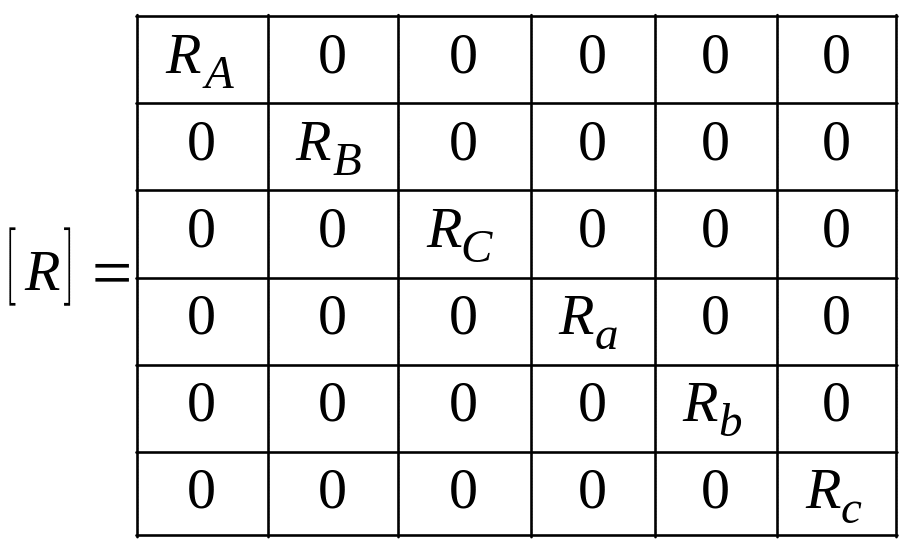; (10.5)

, (10.6)

где - знак транспонирования матрицы; М - взаимная индуктивность между обмотками.

При записи системы дифференциальных уравнений трехфазного АД с короткозамкнутым ротором в фазных координатных осях вводим следующие допущения:

1) обмотка статора получает питание от источника напряжения бесконечной мощности, внутреннее сопротивление которого равно нулю;

2) магнитодвижущие силы (МДС) обмоток синусоидально распределены по окружности статора и ротора;

3) машина симметрична;

4) оси обмоток сдвинуты на угол ;

5) воздушный зазор равномерный;

6) насыщение и потери в стали отсутствуют;

7) параметры обмотки ротора приведены к числу витков и количеству фаз статора.

Таким образом, в основу математической модели трехфазного АД положено не только пространственное расположение обмоток, но и параметры Т-образной схемы замещения фазы АД (рис. 67).

Далее, чтобы не перегружать уравнения множеством индексов, условимся значок приведения параметров « ¢ » не писать.

Обмотку статора подключаем к внешнему источнику, вырабатывающему синусоидальные напряжения

(10.7)

Угловую частоту определяем по формуле

, (10.8)

где - частота напряжения статора.

При короткозамкнутом роторе

. (10.9)

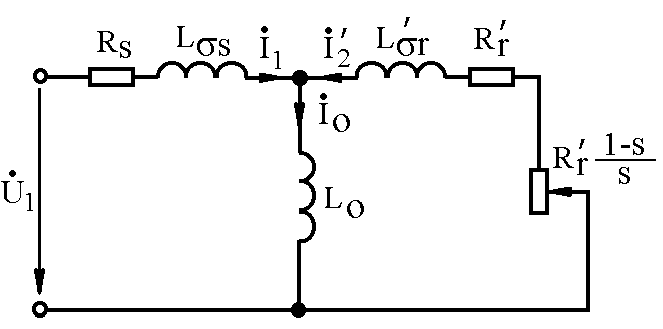
Рис. 67.

На рис. 67: - активное сопротивление обмотки статора; - индуктивность первичной обмотки от потока рассеяния ; - индуктивность намагничивающего контура; - приведенное к статору активное сопротивление обмотки ротора; - приведенная к статору индуктивность обмотки ротора от потока рассеяния ; - сопротивление, учитывающее нагрузку на валу; s – скольжение.

В соответствии с пространственным расположением фаз, указанным на рис. 66, магнитное поле статора будет вращаться против часовой стрелки. В этом же направлении с частотой вращения будет вращаться ротор.

Поскольку обмотки статора и ротора симметричны, то для их активных сопротивлений и индуктивностей можно записать [8]:

; (10.10)

; (10.11)

; (10.12)

. (10.13)

Так как нами было введено допущение о равномерности воздушного зазора, то все собственные индуктивности не зависят от углового положения ротора:

; (10.14)

, (10.15)

где - индуктивность от потока рассеяния; - индуктивность от основного потока.

Рис. 68. Взаимно перемещающиеся катушки

Прежде чем записать выражения взаимных индуктивностей обмоток, рассмотрим две взаимоперемещающиеся катушки с током (рис. 68). Первая катушка неподвижна, а вторая поворачивается относительно первой на некоторый геометрический угол . Каждая из катушек будет создавать свою силу. Направления этих сил указаны на рис. 68 в соответствии с выбранными направлениями токов.

Если вторая катушка вращается относительно первой, то взаимная индуктивность изменяется по закону

(10.16)

и достигает максимума при совпадении осей обмоток.

Таким образом, известная из курса электродинамики формула для электромагнитного момента, создаваемого этими катушками, имеет вид

, (10.17)

где М – взаимная индуктивность.

Взаимное расположение обмоток в электрических машинах переменного тока, как правило, характеризуется электрическим углом:

, (10.18)

тогда (10.17) будет иметь вид

, (10.19)

где - число пар полюсов.

Вернемся к обмоткам рассматриваемого двигателя.

Трехфазные обмотки статора и ротора смещены в пространстве на угол , поэтому

; (10.20)

. (10.21)

Взаимные индуктивности между обмотками статора и ротора являются функциями угла поворота ротора и поэтому являются также функциями времени. Очевидно, что период их изменения равен одному обороту ротора.

Согласно рис. 66 можно записать:

; (10.22)

; (10.23)

; (10.24)

; (10.25)

; (10.26)

. (10.27)

Величина в (10.20)-(10.27) представляет собой максимальное значение взаимной индуктивности и для приведенного АД совпадает по величине с индуктивностью от основного магнитного потока в (10.14), (10.15).

Геометрический угол поворота ротора определяют из уравнения

, (10.28)

где - частота вращения ротора.

Подставив (10.20)-(10.27) в (10.6), получим матрицу индуктивностей , которая записана на с.187.

Матрицу запишем следующим образом:

. (10.29)

Частная производная по углу поворота ротора от пятого элемента первой строки матрицы имеет вид

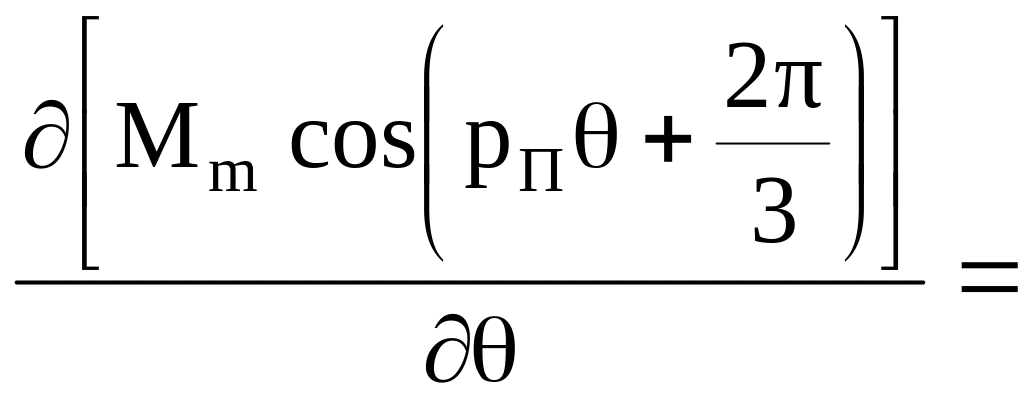
. (10.30)

Аналогично выполняется дифференцирование остальных элементов матрицы . Матрица записана на с. 187.

Таким образом, все матрицы, входящие в систему (10.1), определены.

Дополнив систему (10.1) выражением электромагнитного момента, уравнением движения и уравнением (11.28), получим математическую модель трехфазного АД с короткозамкнутым ротором в фазных осях.

Электромагнитный момент определяем через электромагнитную энергию , сконцентрированную в воздушном зазоре АД [24]:

. (10.31)

Перемножив матрицы в (11.31), получим аналитическое выражение электромагнитного момента трехфазного АД:

EMBED Equation.3 (10.32)

Согласно рекомендациям [12] при моделировании АД в уравнение движения необходимо ввести составляющую, которая учитывает момент трения (механические потери):

, (10.33)

где - номинальная частота вращения; - номинальный момент.

Наличие коэффициента 0,01 в формуле (10.33) оправдано для АД средней и большой мощности. Более значительная доля момента трения возникает в АД малой мощности [12].

Таким образом, система (10.1), уравнение движения (10.33), уравнение (10.28), а также уравнение электромагнитного момента (10.32) представляют собой математическую модель трехфазного АД с короткозамкнутым ротором.

Чтобы проинтегрировать систему (10.1) и уравнения (10.33), (10.28) с учетом (10.32), необходимо задать:

1) все параметры двигателя;

2) законы изменения напряжений , , и статического момента ;

3) начальные условия , , , , , , , ;

4) шаг интегрирования и конечное время.

В результате получим , , , , , , , .

Частота вращения ротора и скорость n связаны следующим соотношением:

, об./мин. (10.34)