3.9. Оптимизация управленческих решений на основе методов исследования операций

Аналитическая часть

Согласно № варианта раскройте один из следующих вопросов.

1. Задачи линейного программирования в операционном и производственном менеджменте.

2. Основные этапы операционного исследования.

3. Геометрическая интерпретация и симплекс-метод решения задач производственного планирования.

4. Задачи дробно-линейного, целочисленного, параметрического программирования.

5. Динамическое программирование в производственном менеджменте.

6. Задача распределения капиталовложений.

7. Задача календарного планирования численности рабочей силы.

8. Изменения в установках, регулирующих действие механизмов и пересмотр количества средств участвующих в операции.

9. Определение зависимости результатов операции от условий ее проведения.

10. Пересмотр использования оборудования.

11. Методы исследования операций.

12. Транспортная задача. Постановка, методы решения.

13. Элементы теории игр.

14. Блочное программирование.

15. Разновидности личностных профилей решений.

Практическая часть

Задание 18. На двух складах А и В имеется соответственно 50 и 40 тн. груза. Требуется спланировать перевозки к трем потребителям (С, D и E) так, чтобы потребитель С получил 30 тн., D–20 тн., E–40 тн., а затраты на перевозку были минимальными.

Исходные данные по вариантам

Таблица 17.

№ варианта	Потребитель С, тн.	Потребитель D, тн.	Потребитель E, тн.
1	10	10	70
2	15	15	60
3	20	10	60
4	25	15	50
5	30	10	50
6	35	25	30
7	40	10	40
8	45	15	30
9	50	10	30
10	55	15	20
11	60	10	20
12	15	25	50
13	20	25	45
14	40	30	20
15	30	30	30

Решение: Составим математическую модель этой задачи.

Математическая модель для решения транспортной задачи

Таблица 18.

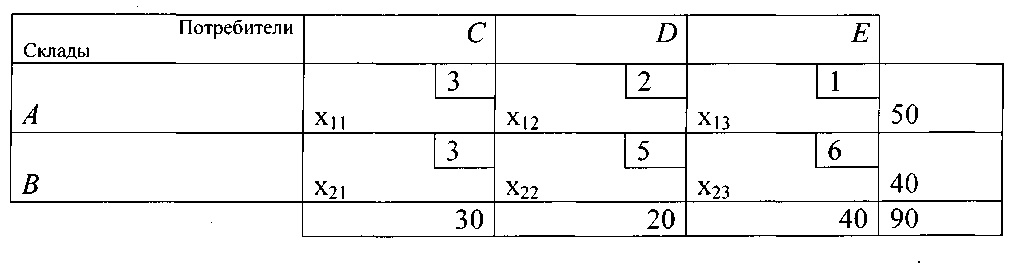
Найдем множество решений системы

(3.9.1)

, то есть все значения должны быть неотрицательными.

Найдем минимальное значение целевой функции

(3.9.2)

Составим методом северо-западного угла первое распределение поставок, начиная с заполнения верхней левой (северо-западной) клетки таблицы. Примем объем перевозки со склада А к потребителю С максимально возможным, исходя из условий задачи, равным 30. Потребитель С полностью удовлетворил свою потребность, соответственно столбец С в табл. 19 можно исключить из дальнейшего рассмотрения.

В таблице поставок найдем новый северо-западный угол – это клетка AD и укажем в ней максимально возможное значение, которое рассчитывается следующим образом: со склада А уже перевезено 30 тн. груза, значит, остаток составляет 50-30=20 тн. Весь груз со склада А перевезен потребителям, и первая строка таблицы поставок исключается из дальнейшего рассмотрения. Потребитель D полностью удовлетворил свою потребность в грузе, и столбец D в табл.19 можно исключить из дальнейшего рассмотрения. В оставшейся части таблицы найдем новый северо-западный угол – это клетка ВЕ и укажем в ней максимально возможное значение (40 тн.). Итак, табл.19 является исходным распределением поставок: .

Первое распределение поставок

Таблица 19.

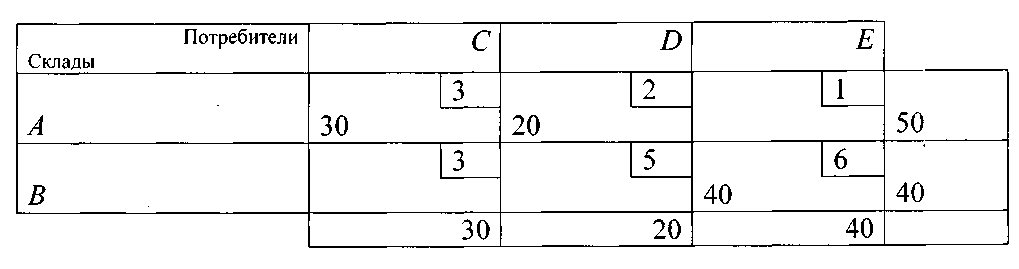
Получим следующее значение целевой функции:

F=30*3+20*2+40*6=370 (руб.).

Проверим полученный результат на оптимальность.

В этой задаче два поставщика (m=2) и три потребителя (n=3). Вычисляем значение выражения для нашей задачи: m+n–1=4.

Из построенной таблицы видно, что число занятых мест равно 3, т.е. меньше значения m+n–1.

Если число занятых клеток после некоторого распределения поставок (совсем необязательно, чтобы это происходило после первого распределения) окажется меньше, чем m+n–1, то с помощью условных поставок, равных нулю, надо заполнить недостающие для выполнения условия клетки, а затем решать как обычно.

Таким образом, по полученному оптимальному плану надо 10 тн. груза со склада А отправить потребителю D и 40 тн. – потребителю Е. Со склада В отправляется 30 тн. потребителю С, а 10 тн. – потребителю D.

Проверка результатов на оптимальность

Таблица 20.

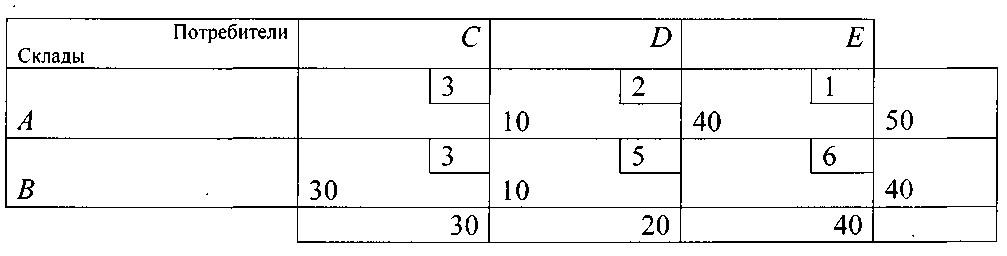
После некоторого числа распределений поставок описанным способом данная задача будет иметь следующее решение:

F=0*3+10*2+40*1+30*3+10*5+0*6=200 (руб.).