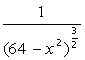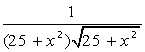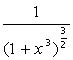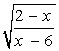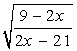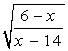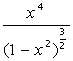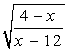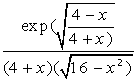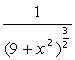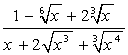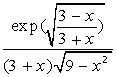Порядок выполнения задания

1. Установите автоматический режим вычислений и режим ото-бражения результатов по горизонтали.

2. Определите подынтегральную функцию как функцию пере-менной х и постройте ее график.

3. Вычислите определенный интеграл.

4. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в левом конце отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.

5. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в правом конце отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.

6. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в середине отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.

7. Сравните полученные значения пределов между собой и со значением интеграла.

8. Постройте графики интегральных сумм как функций числа разбиений отрезка интегрирования.

9. Постройте графики интегральных сумм как функций длины отрезка разбиений.

Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.

Индивидуальное задание к лабораторной работе 9.

Вычислить определенный интеграл непосредственно и с помощью замены переменных.

	f(x)	[a, b]		f(x)	[a, b]
1		[0, 16]	11		[0,4 ]
2		[0, 1]	12		[0,2 ]
3		[0, 5]	13		[0, ]
4		[3, 5]	14		[6, 9]
5		[0, ]	15		[8, 12]
6		[0, ]	16		[6, 10]
7		[0, 4]	17		[0, 3]
8		[0, 2]	18		[1, 64]
9		[0, 4]	19		[0, 3]
10		[0, 5]	20		[0, 1]