
- •Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Случайная величина задана рядом распределения:
- •Найти функцию распределения f(X) и построить ее график.
- •Найти вероятность попадания случайной величины в интервал [2;4).
- •Случайная величина задана рядом распределения:
- •Найти функцию распределения f(X) и построить ее график.
- •Найти вероятность попадания случайной величины в интервал [12;32).
- •Случайная величина задана рядом распределения:
- •Найти функцию распределения f(X) и построить ее график.
- •Найти вероятность попадания случайной величины в интервал [10;30).
- •Случайная величина задана рядом распределения:
- •Найти функцию распределения f(X) и построить ее график.
- •Найти вероятность попадания случайной величины в интервал [1;3).
КОНТРОЛЬНАЯ РАБОТА № 3, задачи 1-7.
Вариант № 1
Вычислить неопределенный интеграл


Вычислить неопределенный интеграл

Вычислить неопределенный интеграл

Вычислить определенный интеграл

Вычислить определенный интеграл

Вычислить определенный интеграл

Решить дифференциальное уравнение

Решить задачу Коши


Исследовать сходимость ряда:


Исследовать ряд на абсолютную и условную сходимость:

Найти область сходимости ряда:

Разложить в ряд по степеням
 функцию:
функцию:

Записать ряд Фурье для периодической, с периодом
 ,
функции:
,
функции:
![]()
Вариант № 2
Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Решить дифференциальное уравнение
 .
.Решить задачу Коши

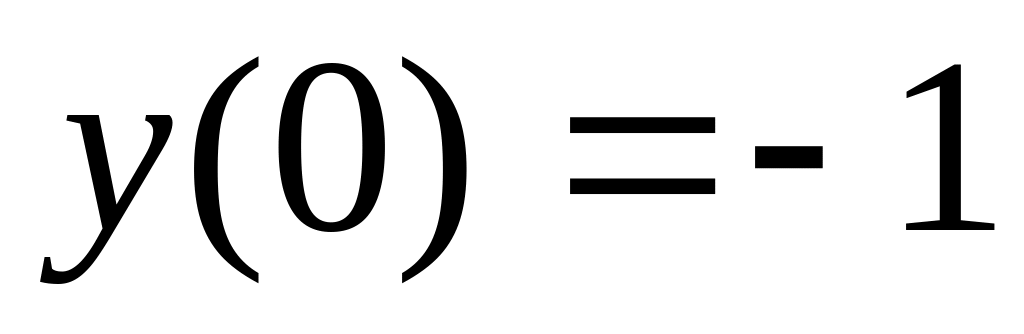 .
.Исследовать сходимость ряда:


 Исследовать
ряд на абсолютную и условную сходимость:
Исследовать
ряд на абсолютную и условную сходимость:
 .
.Найти область сходимости ряда:

Разложить в ряд по степеням функцию:

Записать ряд Фурье для периодической, с периодом , функции:
![]()
Вариант № 3
Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Решить дифференциальное уравнение
 .
.Решить задачу Коши

 .
.Исследовать сходимость ряда:


Исследовать ряд на абсолютную и условную сходимость:

Найти область сходимости ряда:

Разложить в ряд по степеням функцию:

Записать ряд Фурье для периодической, с периодом , функции:
![]()
Вариант № 4
Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Решить дифференциальное уравнение
 .
.Решить задачу Коши

 .
.Исследовать сходимость ряда:


Исследовать ряд на абсолютную и условную сходимость:

Найти область сходимости ряда:

Разложить в ряд по степеням функцию:

Записать ряд Фурье для периодической, с периодом , функции:
![]()
Вариант № 5
Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл .
Вычислить неопределенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Решить дифференциальное уравнение
 .
.Решить задачу Коши

 .
.Исследовать сходимость ряда:


Исследовать ряд на абсолютную и условную сходимость:

Найти область сходимости ряда:

Разложить в ряд по степеням
 функцию:
функцию:

Записать ряд Фурье для периодической, с периодом , функции:
![]()
ВАРИАНТ
№
Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Решить дифференциальное уравнение
 .
.Решить задачу Коши

 .
.Исследовать сходимость ряда:


Исследовать ряд на абсолютную и условную сходимость:

Найти область сходимости ряда:
Разложить в ряд по степеням
 функцию:
функцию:

Записать ряд Фурье для периодической, с периодом , функции:
![]()
ВАРИАНТ
№
Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл

Решить дифференциальное уравнение
 .
.Решить задачу Коши
 .
.Исследовать сходимость ряда:


Исследовать ряд на абсолютную и условную сходимость:

Найти область сходимости ряда:

Разложить в ряд по степеням функцию:

Записать ряд Фурье для периодической, с периодом , функции:
![]()
ВАРИАНТ
№
Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Решить дифференциальное уравнение
 .
.Решить задачу Коши
 .
.Исследовать сходимость ряда:


Исследовать ряд на абсолютную и условную сходимость:

Найти область сходимости ряда:

Разложить в ряд по степеням функцию:

Записать ряд Фурье для периодической, с периодом , функции:
![]()
ВАРИАНТ
№
Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Решить дифференциальное уравнение
 .
.Решить задачу Коши.
 .
.Исследовать сходимость ряда:


Исследовать ряд на абсолютную и условную сходимость:

Найти область сходимости ряда:

Разложить в ряд по степеням функцию:

Записать ряд Фурье для периодической, с периодом , функции:
![]()
ВАРИАНТ
№
Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить неопределенный интеграл
 .
.Вычислить определенный интеграл

Вычислить определенный интеграл
 .
.Вычислить определенный интеграл
 .
.Решить дифференциальное уравнение
 .
.Решить задачу Коши

Исследовать сходимость ряда:


Исследовать ряд на абсолютную и условную сходимость:

Найти область сходимости ряда:

Разложить в ряд по степеням функцию:

Записать ряд Фурье для периодической, с периодом , функции:
![]()
КОНТРОЛЬНАЯ РАБОТА № 4, задачи 1-6
ВАРИАНТ № 1
В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Из ящика вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.
В квадрат со стороной а вписана окружность. Какова вероятность того, что точка, появляющаяся случайным образом в пределах квадрата, окажется внутри круга?
В группе 12 студентов, среди которых 8 отличников. По списку вызывают 9 студентов. Найти вероятность того, что среди вызванных студентов окажется 5 отличников.
Круговая мишень состоит из 3-х зон. Вероятность попадания в I-ю зону - 0,15, во II-ю зону - 0,23, в III-ю зону - 0,17. Какова вероятность промаха?
Таможня имеет 3 таможенных поста. В течение месяца с 1-го поста поступило 40 %, а со 2-го 30 % всех ГТД. Известно, что процент ГТД, оформляемых на экспортные товары на 1-м посту, составляет 20 % от всех ГТД, на 2-м – 30 %, а на 3-м – 10 %. В отделе таможенного оформления из всей совокупности ГТД наудачу выбирается одна декларация. Найти вероятность того, что отобранная декларация относится к экспортному товару.
Случайная величина задана рядом распределения:
xi |
0 |
1 |
2 |
3 |
4 |
рi |
0,01 |
0,25 |
0,35 |
0,26 |
0,13 |
Найти функцию распределения F(x) и построить ее график.
Найти вероятность попадания случайной величины в интервал [1;3).
Определить числовые характеристики случайной величины: математическое ожидание (Mx), дисперсию (Dx), среднее квадратическое отклонение (x).
Решить геометрически задачу линейного программирования: найти mах L, если дано L= – х + З у, х 0,5; 0 y 4; х + у 2; х – y 0
Два типа товаров перевозятся по железной дороге. Для их погрузки выделяются три станции. В таблице указаны:
кол-во перевозимых товаров каждого типа;
возможности станции и время (в сутках), затрачиваемое на погрузку товара на каждой станции.
товары |
станции погрузки |
кол-во перевоз. груза |
||
|
П1 |
П2 |
П3 |
|
Т1 |
1,75 |
2,0 |
1,5 |
13 |
Т2 |
3,5 |
3,0 |
2,5 |
15 |
возможности станции |
14 |
8 |
6 |
|
Определить практически оптимальный вариант использования станции по критерию суммарных затрат времени на погрузку методом линейного программирования.
Найти нижнюю и верхнюю цены игры и минимаксные стратегии. Имеет ли игра решение в чистых стратегиях? (Матрица I).
Решить игру в смешанных стратегиях аналитическим и графическим методами (матрица II).
I. II.
|
|
|
|
|
|
|
|
|
|
3 |
7 |
-1 |
2 |
|
|
0,68 |
1,00 |
А |
-4 |
8 |
3 |
-6 |
|
А |
1,00 |
0,44 |
|
9 |
5 |
-2 |
4 |
|
|
||
ВАРИАНТ № 2
Брошен игральный кубик. Найти вероятность того, что выпадет четное число очков.
В окружность радиуса З см вписан квадрат. Найти вероятность того, что точка поставленная внутрь круга, не окажется в квадрате.
В группе из 30 слушателей на контрольной работе 6 слушателей получили оценку отлично, 10 слушателей - оценку хорошо. 9 слушателей – оценку удовлетворительно. Какова вероятность того, что все 3 слушателя, вызванных к доске, имеют неудовлетворительные оценки по контрольной работе?
Два стрелка, для которых вероятности попадания в мишень соответственно равны 0,7 и 0,8, производят по одному выстрелу по общей мишени. Определить вероятность поражения мишени.
В первой коробке содержится 20 деталей, из них 13 стандартных, во 2-й коробке - 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята деталь и переложена в первую. Найти вероятность того, что деталь, наудачу извлеченная из первой коробки, будет стандартной.
Случайная величина задана рядом распределения:
xi |
0 |
1 |
2 |
3 |
4 |
рi |
0,01 |
0,15 |
0,35 |
0,26 |
0,23 |
Найти функцию распределения F(x) и построить ее график.
Найти вероятность попадания случайной величины в интервал [0;3).
Определить числовые характеристики случайной величины: математическое ожидание (Mx), дисперсию (Dx), среднее квадратическое отклонение (x).
Решить геометрически задачу линейного программирования: найти min L, если дано L= х+Зу, х0, х+4у 4, x+y 6, 0 y 2
Два соединения к новому месту дислокации перевозятся по железной дороге. Для их погрузки выделяются три станции. В таблице указаны:
кол-во перевозимых частей в каждом из соединений;
возможности станции и время ( в сутках), затрачиваемое на погрузку любой части на каждой станции.
соединения |
станции погрузки |
кол-во перевоз. частей |
||
|
П1 |
П2 |
П3 |
|
С1 |
3,0 |
4,0 |
2,5 |
6 |
С2 |
4,5 |
6,5 |
3,5 |
9 |
возможности станции |
6 |
6 |
4 |
|
0пределить практически оптимальный вариант использования станции по критерию суммарных затрат времени на погрузку методом линейного программирования.
Найти нижнюю и верхнюю цены игры и минимаксные стратегии. Имеет ли игра решение в чистых стратегиях? (Матрица I).
Решить игру в смешанных стратегиях аналитическим и графическим методами (матрица II).
I. II.
|
|
|
В |
|
|
|
В |
|
3 |
6 |
1 |
|
|
3 |
2 |
А |
5 |
2 |
3 |
|
А |
-2 |
6 |
|
4 |
2 |
-5 |
|
|
||
ВАРИАНТ № 3
Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.
В круг радиусом R вписан равносторонний треугольник. Какова вероятность того, что поставленная внутри круга точка окажется и внутри треугольника.
Набирая номер телефона, абонент забыл последние две цифры. Какова вероятность, что на6ирая наудачу, номер будет набран правильно, если все цифры номера различные?
Вероятность появления события в одном опыте равна 0,05. Сколько нужно произвести опытов, чтобы событие появилось хотя бы один раз с вероятностью 0,95?
Таможня имеет 3 таможенных поста. В течение месяца с 1-го поста поступило 30 %, со 2-го 10 % всех ГТД. Известно, что процент ГТД, оформляемых на экспортные товары на 1-м посту, составляет 10 % от всех ГТД, на 2-м – 15 %, а на 3-м – 20 %. В отделе таможенного оформления из всей совокупности ГТД наудачу выбирается одна декларация. Найти вероятность того, что отобранная декларация относится к экспортному товару.
Случайная величина задана рядом распределения:
xi |
10 |
15 |
20 |
30 |
40 |
рi |
0,11 |
0,20 |
0,30 |
0,36 |
0,03 |
Найти функцию распределения F(x) и построить ее график.
Найти вероятность попадания случайной величины в интервал [10;30).
Определить числовые характеристики случайной величины: математическое ожидание (Mx), дисперсию (Dx), среднее квадратическое отклонение (x).
Решить геометрически задачу линейного программирования: найти max L, если дано L=х+2у, х0, y0, 4х-2y12, -x+3y6, 2x+4y16.
На складе горючего имеются два пункта налива различной производительности. На склад за горючим прибывает автотранспорт трех типов: 35 - первого, 20-второго и 30 - третьего. Производительность пунктов в минутах и возможности пунктов налива даны в таблице.
Пункты налива |
типы транспорта
|
возможности пункта налива |
||
|
I |
II |
III |
|
№1 |
4 |
6 |
10 |
40 |
№2 |
6 |
9 |
12 |
45 |
количество машин |
35 |
20 |
30 |
|
Используя метод линейного программирования, определить оптимальную организацию налива горючего по критерию времени.
Найти нижнюю и верхнюю цены игры и минимаксные стратегии. Имеет ли игра решение в чистых стратегиях? (Матрица I).
Решить игру в смешанных стратегиях аналитическим и графическим методами (матрица II).
I. II.
|
|
|
В |
|
|
|
|
В |
|
3 |
7 |
-1 |
3 |
|
|
0,608 |
1,000 |
А |
4 |
8 |
0 |
-5 |
|
А |
1,000 |
0,440 |
|
6 |
-9 |
-2 |
4 |
|
|
||
ВАРИАНТ № 4
Брошено две монеты. Какова вероятность появления к гербов (к = 0, 1, 2)?
В треугольник со сторонами, равными а, вписана окружность. Найти вероятность того, что точка, поставленная наудачу внутри треугольника, окажется в круге.
Для участия в шахматном турнире записалось 20 человек. Организаторы отобрали из них команду в 9 человек. Какова вероятность того, что два наиболее сильных шахматиста попадут в команду?
Три стрелка стреляют в одну мишень, при этом известно, что вероятности попадания с одного выстрела соответственно равны: 0,8; 0,7; 0,6. Найти вероятность появления в мишени одной пробоины в результате одновременного выстрела всех трех стрелков.
На склад поступили изделия одного типа, изготовленные на 3-х заводах, причем: с 1-го завода – 50 %, со 2-го завода – 30 % и с 3-го завода 20 %. Известно по статистике, что 1-ый завод в среднем поставляет 0,025 нестандартных изделий, 2-й завод – 0,020 и 3-ий завод – 0,015. Найти вероятность того, сто наудачу взятое изделие со склада соответствует стандарту.
Случайная величина задана рядом распределения:
xi |
11 |
25 |
30 |
35 |
45 |
рi |
0,10 |
0,15 |
0,25 |
0,35 |
0,15 |
Найти функцию распределения F(x) и построить ее график.
Найти вероятность попадания случайной величины в интервал [10;30).
Определить числовые характеристики случайной величины: математическое ожидание (Mx), дисперсию (Dx), среднее квадратическое отклонение (x).
Решить геометрически задачу линейного программирования: найти min L, если дано L= – 2х+у, х0, y0, 3х-2y12, -x+2y8, 2x+3y6.
На двух станциях отправления сосредоточено соответствующее число груза двух типов, который следует доставить в три пункта назначения в количествах, указанных в таблице.
типы груза |
пункты назначения
|
запасы |
||
|
I |
II |
III |
|
1 |
4 |
9 |
3 |
20 |
2 |
4 |
8 |
1 |
30 |
потребности (тыс. тонн) |
10 |
30 |
10 |
|
Используя метод линейного программирования, определить оптимальный план перевозок с минимальными затратами, если в таблице указаны стоимости единицы груза.
Найти нижнюю и верхнюю цены игры и минимаксные стратегии. Имеет ли игра решение в чистых стратегиях? (Матрица I).
Решить игру в смешанных стратегиях аналитическим и графическим методами (матрица II).
I. II.
|
|
|
В |
|
|
|
|
В |
|
-1 |
9 |
6 |
8 |
|
|
0,5 |
0,83 |
А |
-2 |
10 |
4 |
6 |
|
А |
0,75 |
0,5 |
|
5 |
3 |
0 |
7 |
|
|
||
|
7 |
-2 |
8 |
4 |
|
|
||
ВАРИАНТ № 5
