
- •Введение
- •Рекомендуемая литература
- •Тема 1. Кинематика поступательного и вращательного движения §1.1. Кинематика поступательного движения
- •§1.2. Кинематика вращения
- •§1.3. Центр масс
- •Тема 2. Динамика поступательного движения. Элементы специальной теории §2.1. Законы Ньютона
- •§2.2. Силы взаимодействия
- •§2.3. Элементы специальной теории относительности
- •Тема 3. Динамика вращательного движения
- •Тема 4. Работа и энергия. Законы сохранения в механике §4.1. Работа, мощность
- •§4.2. Энергия
- •§4.3. Импульс
- •Тема 5. Распределение Максвелла и Больцмана
- •Тема 6. Средняя энергия молекул
- •Тема 7. Первое начало термодинамики. Работа при изопроцессах
- •Тема 8. Второе начало термодинамики. Энтропия
- •Тема 9. Электростатическое поле в вакууме
- •Тема 10. Законы постоянного тока
- •Закон Ома для неоднородного участка цепи:
- •Тема 11. Магнитостатика. Явление электромагнитной индукции
- •Тема 12. Электрические и магнитные свойства вещества
- •Тема 13. Уравнения Максвелла
- •Тема 14. Свободные и вынужденные колебания. Сложение гармонических колебаний §14.1. Свободные гармонические колебания и их характеристики
- •§14.2. Гармонические осцилляторы
- •§14.3. Сложение свободных гармонических колебаний
- •§14.4. Вынужденные колебания, резонанс
- •Тема 15. Волны. Уравнение волны
- •2.Взаимосвязь длины волны, периода и частоты: , .
- •Тема 16. Электромагнитные волны
- •Тема 17. Интерференция и дифракция света
- •Тема 18. Поляризация и дисперсия света
- •Тема 19. Тепловое излучение. Фотоэффект. Эффект Комптона. Световое давление
- •Тема 20. Спектр атома водорода. Правило отбора
- •Тема 21. Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема 22.Уравнение Шредингера
- •Тема 23. Ядро. Элементарные частицы. Фундаментальные взаимодействия
- •Тема 24. Ядерные реакции. Законы сохранения в ядерных реакциях
Тема 4. Работа и энергия. Законы сохранения в механике §4.1. Работа, мощность
Элементарная
работа силы равна
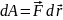 ,
работа на всем перемещении равна
интегралу
,
работа на всем перемещении равна
интегралу
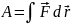 .
.
Работа постоянной силы - скалярное произведение силы и перемещения:
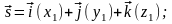

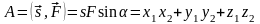
(Скалярное произведение векторов – скалярная величина равная произведению длин векторов на синус угла между ними или сумме произведений соответствующих координат).
Работа переменной силы интеграл от силы по перемещения:
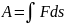 геометрически,равная
площади фигуры под графиком зависимости
силы от перемещения.
геометрически,равная
площади фигуры под графиком зависимости
силы от перемещения.
Мощность – работа, совершаемая за одну секунду
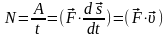 .
.
Единица измерения работы – Джоуль - [A]= Дж; единица измерения мощности – ватт - [N]=Вт.
§4.2. Энергия
В любой физической системе при совершении работы происходит изменение энергии. Энергия – физическая величина, характеризующая состояние системы.
Кинетическая энергия – энергия движения:
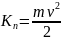 -
кинетическая энергия поступательно
движущегося тела;
-
кинетическая энергия поступательно
движущегося тела;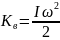 -
кинетическая энергия вращающегося
тела;
-
кинетическая энергия вращающегося
тела;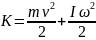 – КЭ
тела движущегося поступательно и
вращающегося (например, колесо автомобиля)
– КЭ
тела движущегося поступательно и
вращающегося (например, колесо автомобиля)
Теорема о кинетической энергии – приращение кинетической энергии частицы на некотором перемещении равно алгебраической сумме работ всех сил, действующих на том же перемещении
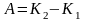 .
.
Отметим, что мощность всех сил, действующих на тело равна скорости изменения кинетической энергии тела
 .
.
Потенциальная энергия – энергия взаимодействия, расчетные формулы для разных видов взаимодействия будут разными, например
а)
потенциальная энергия тела массы m,
поднятого на высоту h над поверхностью
Земли: 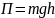
б)
ПЭ гравитационного взаимодействия
двух тел - 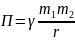 ;
;
в)
ПЭ упруго деформированной пружины - 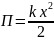 .
.
Теорема о ПЭ – изменение потенциальной энергии взятое с противоположным знаком равно работе сил, действующих на тело:
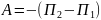 .
.
Если тело движется в потенциальном поле, на него со стороны поля действует сила равная градиенту потенциала поля и направленная противоположно направлению увеличения потенциальной энергии:
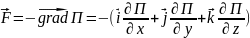 .
.
Закон сохранения механической энергии: в замкнутой системе энергия не исчезает, она превращается из одного вида в другой, полная механическая энергия не изменяется: Е = П+К =const
П ример
4.1.
На рисунке изображены зависимости
ускорений трех прямолинейно движущихся
материальных точек одинаковой массы
от координаты х.
ример
4.1.
На рисунке изображены зависимости
ускорений трех прямолинейно движущихся
материальных точек одинаковой массы
от координаты х.
Для работ A1, A2, A3 сил, действующих на точки, справедливо следующее соотношение:
А1> А2> А3 А1< А2> А3
А1< А2< А3 А1> А2< А3
Решение: по второму закону Ньютона F=ma, т.е. график зависимости ускорения от времени имеет вид графика зависимости силы от времени. Мы отмечали, что работа геометрически равна площади фигуры под графиком зависимости силы от перемещения, т.е. фигура между осью х и линией силы. Самая большая площадь под линией 1, затем 2 и 3, следовательно s1>s2>s3, А1> А2> А3.
П ример
4.2.
На рисунке показан вектор силы, действующей
на частицу. Чему равна работа, совершенная
этой силой при перемещении частицы из
начала координат (0,0) в точку с координатами
(5,2)?
ример
4.2.
На рисунке показан вектор силы, действующей
на частицу. Чему равна работа, совершенная
этой силой при перемещении частицы из
начала координат (0,0) в точку с координатами
(5,2)?
Решение:
по определению
.
Сила постоянна и равна
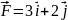 (см.
рис.),
(см.
рис.),
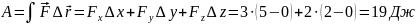 .
.
Пример
4.3.
Частица совершила перемещение из точки
1 с радиус-вектором
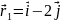 в
точку 2 радиус-вектором
в
точку 2 радиус-вектором
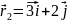 .
При этом на нее действовала сила
.
При этом на нее действовала сила
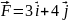 .
Чему равна работа силы7
.
Чему равна работа силы7
Решение: воспользуемся формулой из предыдущего примера
 .
.
Пример
4.4.
Частица движется в двумерном поле,
причем ее потенциальная энергия задается
функцией
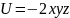 .
Чему равна работа сил поля (в Дж) по
перемещению частицы из точки С(1,1,1) в
точку В(2,2,2)?
.
Чему равна работа сил поля (в Дж) по
перемещению частицы из точки С(1,1,1) в
точку В(2,2,2)?
Решение:
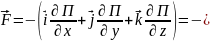 )
)
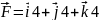 величина
силы равна длине вектора:
величина
силы равна длине вектора:
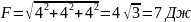 .
.
П ример
4.5.
В потенциальном поле сила Fпропорциональна
потенциальной энергии П. Если график
зависимости потенциальной энергии от
координаты имеет вид (см. рис.), то
зависимость проекции силы Fx
на ось х будет …
ример
4.5.
В потенциальном поле сила Fпропорциональна
потенциальной энергии П. Если график
зависимости потенциальной энергии от
координаты имеет вид (см. рис.), то
зависимость проекции силы Fx
на ось х будет …

Решение:
потенциальная энергия линейно зависит
от координаты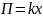 .
Проекция силы на ось х равна производной
энергии по координате, взятой с
противоположным знаком:
.
Проекция силы на ось х равна производной
энергии по координате, взятой с
противоположным знаком:
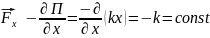 Ответ:
график (1).
Ответ:
график (1).
Пример 4.6.Тело массы m=100 г бросили с поверхности земли с начальной скоростью V0= 10 м/с под углом α=30° к горизонту. Если пренебречь сопротивлением воздуха, средняя мощность, развиваемая силой тяжести за время падения тела на землю, равна …
Решение:
мощность – это изменение энергии за
единицу времени
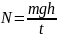 .
Потенциальная энергия в верхней точке
траектории равна кинетической энергии
в начальный момент
.
Потенциальная энергия в верхней точке
траектории равна кинетической энергии
в начальный момент 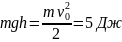 .
.
Время падения равно времени подъема. В верхней точке траектории vyобращается в ноль, используем формулу скорости:
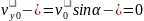 ;
; 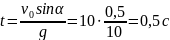
Ответ: 
Пример 4.7. Диск в одном случае скатывается без проскальзывания с наклонной плоскости высотой h, а в другом случае соскальзывает с нее. Если трением можно пренебречь, то отношение скоростей диска v1/v2у основания наклонной плоскости будет равно:
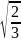
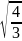

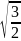
Решение:
1) диск скатывается без проскальзывания
т.е. движется поступательно и вращается
– кинетическая энергия
,
вспомним  , момент
инерции диска
.
Кинетическая энергия
внизу равна потенциальной энергии в
верхней точке наклонной плоскости:
, момент
инерции диска
.
Кинетическая энергия
внизу равна потенциальной энергии в
верхней точке наклонной плоскости:
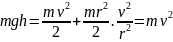 ,
, 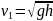 .
.
2)диск соскальзывает, т.е. движется поступательно -
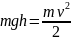 ,
, 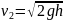 .
.
Отношение
скоростей, равно: 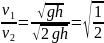 .
.
Пример 4.8.Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки высотой h. Тогда верным утверждением относительно времени скатывания к основанию горки является следующее:
быстрее скатится полый цилиндр
быстрее скатится сплошнойцилиндр
оба тела скатятся одновременно
Решение: время скатывания тем меньше, чем больше скорость тела к конце горки. При скатывании происходит превращение потенциальной энергии в кинетическую
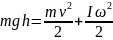 ,
, 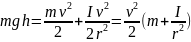 ,
,
Из
последнего выражения следует, что
конечная скорость будет больше для тела
с меньшим моментом инерции. Момент
инерции полого цилиндра(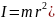 большемомента
инерции сплошного цилиндра (
),
значит, сплошной цилиндр скатится
быстрее.
большемомента
инерции сплошного цилиндра (
),
значит, сплошной цилиндр скатится
быстрее.
Пример 4.9.Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Если начальные скорости тел одинаковы, то какой цилиндр поднимется выше и чему равно отношение высот h1/h2 …
7/10 14/15 ¾ 1
Решение:
при движении вверх происходит превращение
кинетической энергии в потенциальную,
см. формулы предыдущего задания:  ,
выше
поднимется тело с большей кинетической
энергией, т.е. большим моментом инерции
- полый цилиндр. Отношение
высот равно:
,
выше
поднимется тело с большей кинетической
энергией, т.е. большим моментом инерции
- полый цилиндр. Отношение
высот равно:
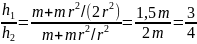 .
.
