§2.3. Элементы специальной теории относительности
При описании движения тел со скоростями близкими с скорости света в вакууме необходимо перейти от классической механики к релятивистской, в основе которой лежат постулаты Эйнштейна:
Принцип относительности – никакие опыты, проведенные внутри инерциальной системы отсчета, не дают возможности обнаружит, покоится эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой;
Принцип инвариантности скорости света – скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.
Это означает, что для наблюдателя находящегося внутри движущегося со скоростью близкой к скорости света космического корабля все процессы происходят так как если бы он был неподвижен. Для наблюдателя на Земле длины предметов на корабле уменьшаются, а массы тел и интервалы времени событий увеличиваются:
; 
; 
,
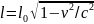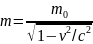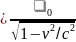где m0, l0 , 0 – масса, длина тела, длительность промежутка времени в системе относительно которой тело покоится.
Релятивистский закон сложения скоростей:
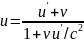
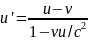
скорость тела относительно неподвижной системы отсчета (u), скорость тела относительно движущейся системы отсчета (u’), скорость подвижной системы отсчета относительно неподвижной (v)
Пример 2.7. Скорость света в вакууме:
зависит от длины волны
одинакова во всех инерциальных системах отсчета
различна в разных системах отсчета
зависит от скорости источника
П
ример
2.8.На
борту космического корабля нанесена
эмблема в виде круга (рис. а).Если корабль
движется в направлении, указанном на
рисунке стрелкой, со скоростью, сравнимой
со скоростью света, то какую форму примет
эмблема в неподвижной системе отсчета?
Ответ:из-за релятивистского сокращения длины в направлении движения корабля эта эмблема примет форму эллипса сжатого в направлении скорости (рис.б).
Пример 2.9.Космический корабль с двумя космонавтами летит со скоростью V=0,8c (c - скорость света в вакууме). Один из космонавтов медленно поворачивает метровый стержень из положения 1, параллельного направлению движения, в положение 2, перпендикулярное этому направлению. Тогда длина стержня с точки зрения другого космонавта …
Ответ: не изменится, так как оба наблюдателя находятся в одной системе отчета, относительно которой стержень неподвижен.
Пример 2.10.Космический корабль пролетает мимо Вас со скоростью 0,8с. По Вашим измерениям его длина равна 90 м. Чему равна его длина в состоянии покоя?
Решение: выведем формулу для расчета длины корабля относительно неподвижной системы отсчета из формулы: ,
получим
выражение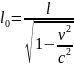 
,
подставим значение скорости
.
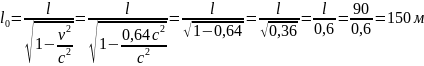Пример 2.11. Релятивистское сокращение длины ракеты составляет N=20%. При этом скорость ракеты равна…
Решение:релятивистское сокращение длины ракеты выраженное в процентах – это отношение изменения длины ракеты к ее первоначальной длине умноженное на сто
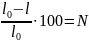
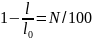
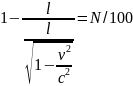
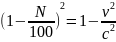
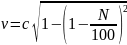
Ответ: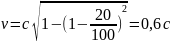 
Пример 2.12.Ускоритель сообщил радиоактивному ядру скорость 0,4с (с – скорость света в вакууме). В момент вылета из ускорителя ядро выбросило в направлении своего движения -частицу, скорость которой 0,75с относительно ускорителя. Скорость -частицы относительно ядра равна…
Решение: при решении задачи нужно найти скорость тела (-частицы, u’=?) относительно подвижной системы отсчета (относительно ядра, v=0,4c), если известна скорость частицы относительно неподвижной системы отсчета (u=0,75с).Воспользуемся формулой
Ответ:
.
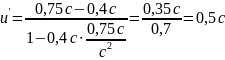Пример 2.13.Движущееся со скоростью 0,6с ядро испустило частицу в направлении своего движения. Скорость частицы относительно ядра 0,3с. Тогда ее скорость относительно неподвижной системы отсчета равна…
Решение: u=?; v=0,6c; u’=0,3c.
Ответ:
=