
- •Введение
- •Рекомендуемая литература
- •Тема 1. Кинематика поступательного и вращательного движения §1.1. Кинематика поступательного движения
- •§1.2. Кинематика вращения
- •§1.3. Центр масс
- •Тема 2. Динамика поступательного движения. Элементы специальной теории §2.1. Законы Ньютона
- •§2.2. Силы взаимодействия
- •§2.3. Элементы специальной теории относительности
- •Тема 3. Динамика вращательного движения
- •Тема 4. Работа и энергия. Законы сохранения в механике §4.1. Работа, мощность
- •§4.2. Энергия
- •§4.3. Импульс
- •Тема 5. Распределение Максвелла и Больцмана
- •Тема 6. Средняя энергия молекул
- •Тема 7. Первое начало термодинамики. Работа при изопроцессах
- •Тема 8. Второе начало термодинамики. Энтропия
- •Тема 9. Электростатическое поле в вакууме
- •Тема 10. Законы постоянного тока
- •Закон Ома для неоднородного участка цепи:
- •Тема 11. Магнитостатика. Явление электромагнитной индукции
- •Тема 12. Электрические и магнитные свойства вещества
- •Тема 13. Уравнения Максвелла
- •Тема 14. Свободные и вынужденные колебания. Сложение гармонических колебаний §14.1. Свободные гармонические колебания и их характеристики
- •§14.2. Гармонические осцилляторы
- •§14.3. Сложение свободных гармонических колебаний
- •§14.4. Вынужденные колебания, резонанс
- •Тема 15. Волны. Уравнение волны
- •2.Взаимосвязь длины волны, периода и частоты: , .
- •Тема 16. Электромагнитные волны
- •Тема 17. Интерференция и дифракция света
- •Тема 18. Поляризация и дисперсия света
- •Тема 19. Тепловое излучение. Фотоэффект. Эффект Комптона. Световое давление
- •Тема 20. Спектр атома водорода. Правило отбора
- •Тема 21. Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема 22.Уравнение Шредингера
- •Тема 23. Ядро. Элементарные частицы. Фундаментальные взаимодействия
- •Тема 24. Ядерные реакции. Законы сохранения в ядерных реакциях
Тема 16. Электромагнитные волны
1. Уравнение плоской электромагнитной волны
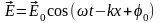 ;
;
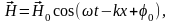
где и
и
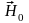 ―
соответственно амплитуды напряженности
электрического и магнитного полей
волны.
―
соответственно амплитуды напряженности
электрического и магнитного полей
волны.
2. Скорость распространения электромагнитной волны:
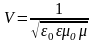 ,где
— диэлектрическая проницаемость среды;
0
― электрическая постоянная;
— магнитная проницаемость среды; 0
― магнитная постоянная;
;
,где
— диэлектрическая проницаемость среды;
0
― электрическая постоянная;
— магнитная проницаемость среды; 0
― магнитная постоянная;
;
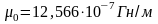 .
Для вакуума
.
Для вакуума
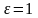 ;
;
;
;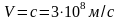 .
.
3. Плотность энергии электромагнитной волны
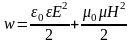 или
или
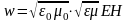 ,
,
где
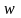 ― плотность энергии электромагнитной
волны,
— абсолютный показатель преломления
среды.
― плотность энергии электромагнитной
волны,
— абсолютный показатель преломления
среды.
Пример
16.1.Если
в электромагнитной волне, распространяющейся
в среде с показателем преломления n=2,
значения напряженностей электрического
и магнитного полей соответственно равны
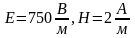 ,
то плотность энергии составляет …
,
то плотность энергии составляет …
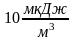
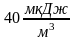
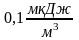
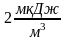
Решение: связь плотности энергии электромагнитной волны с показателем преломления среды можно выразить соотношением , где ― плотность энергии электромагнитной волны, — абсолютный показатель преломления среды.
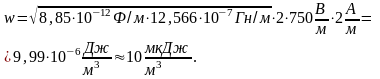
Пример
16.2.
Если в электромагнитной волне,
распространяющейся в вакууме. Значение
напряженности электрического поля
равно:
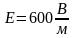 ,
плотность энергии электромагнитной
волны
,
плотность энергии электромагнитной
волны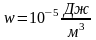 ,
то напряженность магнитного поля
составляет …
,
то напряженность магнитного поля
составляет …
0,37А/м 3,66 А/м 36,60 В/м 0,37 В/м
Решение:
плотность
энергии электромагнитной волны
,
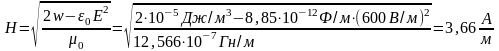 4.
Плотность
потока энергии электромагнитной волны
(векторУмова - Пойнтинга):
4.
Плотность
потока энергии электромагнитной волны
(векторУмова - Пойнтинга):  .
.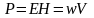
Пример 16.3. При уменьшении в 3 раза амплитуды колебаний векторов напряженности электрического и магнитного полей плотность потока энергии …
уменьшится в 6 раз; увеличится в 6 раз;
уменьшится в 9 раз; не изменится
Решение:
плотность потока энергии электромагнитной
волны
 .
.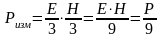 ,
плотность потока энергии уменьш. в 9
раз.
,
плотность потока энергии уменьш. в 9
раз.
Тема 17. Интерференция и дифракция света
Интерференция наблюдается при наложении двух или нескольких световых пучков. Необходимым условием интерференции волн - является когерентность, т.е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.
Уравнение
монохроматической волны:
где
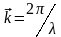 -
волновой вектор и
-
волновой вектор и
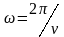 - циклическая частота волны. При
сложении двух волн:
- циклическая частота волны. При
сложении двух волн:
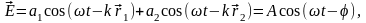
амплитуда результирующей волны:
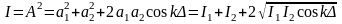 ,
,
где
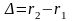 - разность хода двух волн.
- разность хода двух волн.
Интерференционный максимум наблюдается при условии, что разность хода двух лучей кратна длине волны (=m, m=0, ±1, ±2, …)
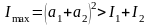 ,
,
Интерференционный минимум при условии, что на разности хода лучей укладывается нечетное число полуволн (=(2m+1)/2),
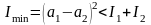 .
.
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Согласно принципу Гюйгенса–Френеля: каждая точка, до которой доходит волна, становится центром вторичных волн, а вторичные волны, приходя в точку наблюдения, интерферируют друг с другом.
Пример 17.1. На дифракционную решетку по нормали к ее поверхности падает плоская световая волна с длинной волны λ. Если постоянная решетки d = 4,5λ, то наибольший порядок максимума, наблюдаемого в фокальной плоскости собирающей линзы, равен …
Решение:
Условие
главных максимумов для дифракционной
решетки имеет вид 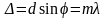 ,
где d –
период решетки, φ –
угол дифракции, m –
порядок максимума, λ –
длина световой волны. Из этого условия
следует, что наибольший порядок
дифракционного максимума будет при
максимальном значении синуса.
Поскольку sin φ не
может быть больше единицы, d ≥ mλ.
Из условия d = 4,5λ;
следует, что m ≤ d/λ=4,5.
Если
учесть, что порядок максимума является
целым числом, то mmax =
4. Тогда общее число максимумов, получаемых
при дифракции на решетке, N = 2mmax+1 = 9.
,
где d –
период решетки, φ –
угол дифракции, m –
порядок максимума, λ –
длина световой волны. Из этого условия
следует, что наибольший порядок
дифракционного максимума будет при
максимальном значении синуса.
Поскольку sin φ не
может быть больше единицы, d ≥ mλ.
Из условия d = 4,5λ;
следует, что m ≤ d/λ=4,5.
Если
учесть, что порядок максимума является
целым числом, то mmax =
4. Тогда общее число максимумов, получаемых
при дифракции на решетке, N = 2mmax+1 = 9.
П ример
17.2.
При
дифракции на дифракционной решетке с
периодом d,
равным 0.004 мм, наблюдается зависимость
интенсивности монохроматического
излучения от синуса угла дифракции,
представленная на рисунке (изображены
только главные максимумы).Длина волны
монохроматического излучения равна
_____ нм.
ример
17.2.
При
дифракции на дифракционной решетке с
периодом d,
равным 0.004 мм, наблюдается зависимость
интенсивности монохроматического
излучения от синуса угла дифракции,
представленная на рисунке (изображены
только главные максимумы).Длина волны
монохроматического излучения равна
_____ нм.
Решение:
Условие
главных максимумов для дифракционной
решетки имеет вид
,
где d –
период решетки, φ –
угол дифракции, m –
порядок максимума, λ –
длина световой волны.
Отсюда
длина волны монохроматического излучения
равна: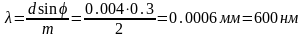
Пример 17.3.На узкую щель шириной d падает нормально плоская световая волна с длиной волны λ. На рисунке схематически представлена зависимость интенсивности света от синуса угла дифракции. Тогда отношение d/λ равно…
Р ешение:
Ширина центрального максимума равна
расстоянию между минимумами первого
порядка. Условие
главных максимумов для дифракционной
решетки имеет вид
,
где d –
период решетки, φ –
угол дифракции, m –
порядок максимума, λ –
длина световой волны. Из
рисунка для минимума первого порядка
sin φ1 = 0.2.
Bз
условия минимумов для дифракции
sin φ1 = λ/d = 0.2,
тогда d/λ = 5.
ешение:
Ширина центрального максимума равна
расстоянию между минимумами первого
порядка. Условие
главных максимумов для дифракционной
решетки имеет вид
,
где d –
период решетки, φ –
угол дифракции, m –
порядок максимума, λ –
длина световой волны. Из
рисунка для минимума первого порядка
sin φ1 = 0.2.
Bз
условия минимумов для дифракции
sin φ1 = λ/d = 0.2,
тогда d/λ = 5.
Пример
17.4.Тонкая
стеклянная пластинка с показателем
преломления n = 1.5 и
толщиной d = 2 мкм помещена
между двумя средами с показателями
преломления n1 = 1.2 и n2 = 1.3 На
пластинку по нормали падает свет с
длиной волны λ = 600 нм.
Разность
хода интерферирующих отраженных лучей
( в нм)
равна …
в нм)
равна …
Решение:
разность
хода лучей, отраженных от верхней и
нижней граней пластинки, равна Δ = 2dn .
С
учетом изменения фазы колебаний на π при
отражении от оптически более плотной
среды (в нашем случае при отражении от
верхней грани пластинки) разность хода
будет равна: 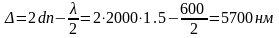 .
.
Пример 17.5. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке (установка для наблюдения колец Ньютона). Если на плоскую поверхность линзы падает нормально свет с длиной волны 0,6 мкм, то толщина воздушного зазора (в нм) в том месте, где в отраженном свете видно первое темное кольцо, равна
Решение:
Условие интерференционного минимума
для колец Ньютона:
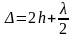 ,
где Δ –
оптическая разность хода интерферирующих
лучей, h –
толщина воздушного зазора, λ –
длина световой волны. Темные кольца
наблюдаются только в случае, когда
оптическая разность хода равна начетному
числу длин волн:
,
где Δ –
оптическая разность хода интерферирующих
лучей, h –
толщина воздушного зазора, λ –
длина световой волны. Темные кольца
наблюдаются только в случае, когда
оптическая разность хода равна начетному
числу длин волн:
 ,
где n –
порядок минимума.
,
где n –
порядок минимума.
Минимальной толщине воздушного зазора соответствует n = 1, тогда h = λ/2 = 300 нм.
