
- •Введение
- •Рекомендуемая литература
- •Тема 1. Кинематика поступательного и вращательного движения §1.1. Кинематика поступательного движения
- •§1.2. Кинематика вращения
- •§1.3. Центр масс
- •Тема 2. Динамика поступательного движения. Элементы специальной теории §2.1. Законы Ньютона
- •§2.2. Силы взаимодействия
- •§2.3. Элементы специальной теории относительности
- •Тема 3. Динамика вращательного движения
- •Тема 4. Работа и энергия. Законы сохранения в механике §4.1. Работа, мощность
- •§4.2. Энергия
- •§4.3. Импульс
- •Тема 5. Распределение Максвелла и Больцмана
- •Тема 6. Средняя энергия молекул
- •Тема 7. Первое начало термодинамики. Работа при изопроцессах
- •Тема 8. Второе начало термодинамики. Энтропия
- •Тема 9. Электростатическое поле в вакууме
- •Тема 10. Законы постоянного тока
- •Закон Ома для неоднородного участка цепи:
- •Тема 11. Магнитостатика. Явление электромагнитной индукции
- •Тема 12. Электрические и магнитные свойства вещества
- •Тема 13. Уравнения Максвелла
- •Тема 14. Свободные и вынужденные колебания. Сложение гармонических колебаний §14.1. Свободные гармонические колебания и их характеристики
- •§14.2. Гармонические осцилляторы
- •§14.3. Сложение свободных гармонических колебаний
- •§14.4. Вынужденные колебания, резонанс
- •Тема 15. Волны. Уравнение волны
- •2.Взаимосвязь длины волны, периода и частоты: , .
- •Тема 16. Электромагнитные волны
- •Тема 17. Интерференция и дифракция света
- •Тема 18. Поляризация и дисперсия света
- •Тема 19. Тепловое излучение. Фотоэффект. Эффект Комптона. Световое давление
- •Тема 20. Спектр атома водорода. Правило отбора
- •Тема 21. Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема 22.Уравнение Шредингера
- •Тема 23. Ядро. Элементарные частицы. Фундаментальные взаимодействия
- •Тема 24. Ядерные реакции. Законы сохранения в ядерных реакциях
Тема 15. Волны. Уравнение волны
1.Уравнение плоской бегущей волны, распространяющейся вдоль положительного направления оси х
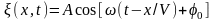 или
или
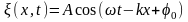 ,
,
г де
де
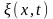 — смещение точек среды с координатой
х
в момент времени t;
A
― амплитуда;
— смещение точек среды с координатой
х
в момент времени t;
A
― амплитуда;
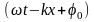 — фаза;
— фаза;
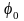 ― начальная фаза;
― начальная фаза;
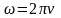 — круговая частота; =1/Т
– частота; Т – период колебаний;
— круговая частота; =1/Т
– частота; Т – период колебаний;
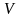 ― скорость распространения колебаний
в среде (фазовая скорость);
― скорость распространения колебаний
в среде (фазовая скорость);
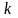 — волновое число
— волновое число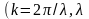 ― длина волны).
― длина волны).
Пример
15.1.
На рисунке представлен профиль поперечной
бегущей волны, которая распространяется
со скоростью
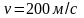 .
Амплитуда скорости колебаний точек
среды (в м/с) равна …
.
Амплитуда скорости колебаний точек
среды (в м/с) равна …
0,05 м/с 6,28 м/с
12,56 м/с 200 м/с
Решение:уравнение
плоской бегущей волны, распространяющейся
вдоль положительного направления оси
х:
.
В этом уравненииА
— амплитуда волны, а амплитуда скорости
колебаний точек среды, соответственно
составит Vm
= Aω.
Из рисунка можно определить λ=10
м. Известно соотношение между длиной
волны λ и циклической частотой: .
Амплитуду волны определим по рисунку:
А=0,05
м. Следовательно
.
Амплитуду волны определим по рисунку:
А=0,05
м. Следовательно
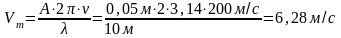 .
.
П ример 15.2. На рисунке представлен профиль поперечной упругой бегущей волны. Согласно рисунку значение волнового числа равно …
2,512 м-1 0,628 м-1 1,256 м-1 0,314 м-1
Решение:
уравнение
плоской бегущей волны, распространяющейся
вдоль положительного направления оси
х:
.
Из рисунка можно определить λ=10м.
Волновое число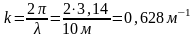 .с
периодом и частотой
.с
периодом и частотой
2.Взаимосвязь длины волны, периода и частоты: , .
3.
Разность фаз колебаний двух точек среды
: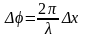 ,
,
Где х – расстояние между колеблющимися точками (разность хода).
4. Фазовая скорость волны:
а)
продольных волн (распространяющихся в
упругой среде и твердых телах):
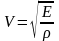 , гдеЕ
— модуль Юнга; ρ ― плотность вещества;
, гдеЕ
— модуль Юнга; ρ ― плотность вещества;
б) поперечных волн:
 ,где
G
— модуль сдвига;
,где
G
— модуль сдвига;
в)
в газах: 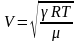 ,где
γ — показатель адиабаты (γ = ср
/ сv);
R
― универсальная газовая постоянная;
T—
термодинамическая температура; μ ―
молярная масса вещества.
,где
γ — показатель адиабаты (γ = ср
/ сv);
R
― универсальная газовая постоянная;
T—
термодинамическая температура; μ ―
молярная масса вещества.
5.
Плотность энергии упругой волны:
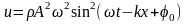 .
.
6.
Средняя
по времени плотность энергии волны: 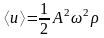 .
.
Пример
15.3.
В упругой среде плотностью
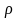 распространяется
плоская синусоидальная волна с частотой
распространяется
плоская синусоидальная волна с частотой
 и амплитудой
и амплитудой
 .
При переходе волны в другую среду,
плотность которой в 2 раза меньше,
амплитуду увеличивают в 4 раза, тогда
объемная плотность энергии, переносимой
волной, …
.
При переходе волны в другую среду,
плотность которой в 2 раза меньше,
амплитуду увеличивают в 4 раза, тогда
объемная плотность энергии, переносимой
волной, …
увеличится в4 раза, увеличится в 8 раз,
уменьшится в 2 раза, не изменится.
Решение: среднее значение объемной плотности энергии равно: . За счет уменьшения плотности среды объемная плотность энергии уменьшится в 2 раза, а за счет увеличения амплитуды – увеличится в 16 раз, следовательно, объемная плотность энергии увеличится в 8 раз.
7. Плотность потока энергии волны (вектор Умова)
а)
мгновенное значение
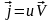 ,
,
где
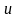 — плотность энергии упругой волны,
— плотность энергии упругой волны,
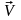 ― фазовая скорость (скорость распространения
волны).
― фазовая скорость (скорость распространения
волны).
б)
среднее значение
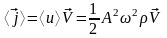 ,
,
где
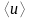 — средняя
по времени плотность энергии волны,
― фазовая скорость.
— средняя
по времени плотность энергии волны,
― фазовая скорость.
Пример 15.4. В физиотерапии используется ультразвук частотой 800 кГц и интенсивностью 1 Вт/м2. При этом скорость ультразвуковых волн в теле человека равна 1500 м/с. При воздействии таким ультразвуком на мягкие ткани человека плотностью 1060 кг/м3 амплитуда колебаний молекул будет равна …
2,2 Å 0,22 Å 44 Å 4,4 Å
Решение:
Интенсивностью волны называется
скалярная величина, равная модулю
среднего значения вектора плотности
потока энергии (вектора Умова)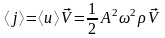 ,
где
— средняя
по времени плотность энергии волны, A
― амплитуда;
― фазовая скорость,
— круговая частота; ρ ― плотность
вещества (среды). Тогда из соотношения
,
где
— средняя
по времени плотность энергии волны, A
― амплитуда;
― фазовая скорость,
— круговая частота; ρ ― плотность
вещества (среды). Тогда из соотношения
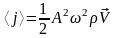 можно определить амплитуду
можно определить амплитуду
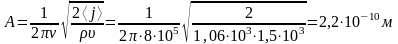 =
2,2
Å.
=
2,2
Å.
Пример
15.5.
Плоская
электромагнитная волна распространяется
в диэлектрике с проницаемостью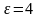 .
Если амплитудное значение электрического
вектора волны
.
Если амплитудное значение электрического
вектора волны
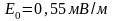 ,
то интенсивность волны равна …(
,
то интенсивность волны равна …(
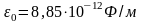 .)
.)
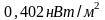

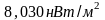

Решение:
интенсивностью
волны называется скалярная величина,
равная модулю среднего значения вектора
плотности потока энергии (вектора Умова
– Пойнтинга)
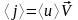 ,
где
—
средняя
по времени плотность энергии волны,
― фазовая скорость. Среднее значение
объемной плотности энергии электромагнитной
волны определяется выражением
,
где
—
средняя
по времени плотность энергии волны,
― фазовая скорость. Среднее значение
объемной плотности энергии электромагнитной
волны определяется выражением
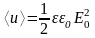 ,
а скорость волны в среде
,
а скорость волны в среде
 ,
где
,
где
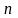 ― абсолютный показатель преломления
среды, причем
― абсолютный показатель преломления
среды, причем
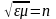 .
Для неферромагнитных сред
.
Для неферромагнитных сред
 .
Таким образом, выражение для интенсивности
электромагнитной волны можно представить
в виде
.
Таким образом, выражение для интенсивности
электромагнитной волны можно представить
в виде

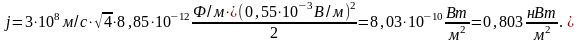
8.
Уравнение
стоячей волны
: 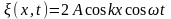 .
.
