Министерство образования и науки, молодёжи и спорта Украины
Севастопольский национальный технический университет
Факультет радиоэлектроники
Кафедра радиотехники и телекоммуникаций
Расчетно-Графическое Задание №1
по дисциплине
«Устройства СВЧ и антенны»
Вариант - 07
Выполнил: студент гр. Р-31д
Зименков Александр
Николаевич
Принял: Головин В.В.
Севастополь
2013
1. ЗАДАЧА №1
Исследование режимов работы линии передачи
Линия передачи
длиной
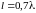с волновым сопротивлением ρ = 75 Ом
нагружена на сопротивление
.
Необходимо:
а) построить графики распределений вдоль линии передачи амплитуд напряжения и тока, когда значение сопротивления нагрузки:
;
;
;
б) построить графики распределений вдоль линии передачи активной и реактивной составляющих сопротивления Z(x), когда значение сопротивления нагрузки:
;
;
.
1.1. Сопротивление нагрузки
Для того чтобы построить необходимые зависимости, следует сначала определить модуль и аргумент коэффициента отражения сигнала в нагрузке по напряжению. Формула для расчета коэффициента отражения в нагрузке имеет вид
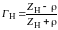(1.1)
Используя вычислительные возможности программного пакета MathCAD, получим:
; (1.2)
. (1.3)
Выражения для распределений напряжения и тока вдоль линии передачи в нормированном виде представлены ниже:
(1.4)
(1.5)
Подставляя в эти выражения рассчитанные значения 1.2 и 1.3, получим графики распределения напряжения и тока вдоль линии передачи (рис 1.1).
Рис. 1.1 ― График распределения напряжения и тока в линии передачи при нагрузке
Распределение комплексного сопротивления вдоль линии передачи можно рассчитать по формуле
(1.6)
Из этого выражения, известным способом, подставляя числовые значения, определим модуль и аргумент комплексного сопротивления, а также построим графики распределения модуля и аргумента комплексного сопротивления вдоль линии передачи (рис 1.2 и 1.3).
Рис. 1.2 ― График распределения активной составляющей комплексного сопротивления линии передачи при нагрузке
Рис. 1.3 ― График распределения реактивной составляющей комплексного сопротивления линии передачи при нагрузке
1.2. Сопротивление нагрузки
Модуль и аргумент коэффициента отражения в нагрузке определим так же, как и в предыдущем пункте. Получим:
; (1.7)
. (1.8)
Используя выражения 1.4 и 1.5, а также рассчитанные значения 1.7 и 1.8, построим графики распределения напряжения и тока вдоль линии передачи (рис 1.4).
Рис. 1.4 ― График распределения напряжения и тока в линии передачи при нагрузке
Используя выражение 1.6 и известные числовые значения, построим графики распределения модуля и аргумента комплексного сопротивления вдоль линии передачи (рис 1.5 и 1.6).
Рис. 1.5 ― График распределения активной составляющей комплексного сопротивления линии передачи при нагрузке
Рис. 1.6 ― График распределения реактивной составляющей комплексного сопротивления линии передачи при нагрузке