4.2 Проверка устойчивости аср по критерию Гурвица
Критерий Гурвица относится к алгебраическим критериям.
При его использовании из коэффициентов характеристического уравнения (9) составляют матрицу (главный определитель Гурвица) по следующему правилу: по главной диагонали слева направо выписывают все коэффициенты характеристического уравнения от а1 до an в порядке возрастания индексов. Затем каждый столбец дополняют так, чтобы вверх от диагонали индексы коэффициентов увеличивались на 1, а вниз уменьшались. Вместо коэффициентов с индексом меньше 0 и больше n пишут 0.
а1 а3
а5 . . 0
0
а0 а2
а4
. . 0 0
Δn = 0 а1 а3 . . . 0 0 (10)
. . . . . . . .
. . . . . . . .
0 0 0 . . .
аn-1 0
0 0 0 . . . an-2 an
Выделяя в главном определителе диагональные миноры, отчеркивая строки и столбцы, как показано в (10), получаем определители Гурвица низшего порядка
а1 а3
а1 а3
а5
Δ1 = а1 , Δ2 = , Δ3 = а0 а2 а4 , . . . . (11) а0 а2 0 а1 а3
Номер определителя Гурвица зависит от номера коэффициента по диагонали, до которого составляют данный определитель.
Для устойчивости системы необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры при а0 >0 были положительны, т.е. Δ1 > 0, Δ2 > 0, Δ3 > 0, . . . , Δn > 0.
Ниже приведены условия устойчивости для систем первого, второго, третьего и четвертого порядков:
- для системы первого порядка (n=1) а0 > 0 , а1 > 0;
- для системы второго порядка (n=2) а0 > 0 , а1 > 0, а2 > 0;
- для системы третьего порядка (n=3) а0 > 0 , а1 > 0, а2 > 0,
а3 > 0, а1 а3 - а0 а1 > 0 ;
- для системы четвертого порядка (n=4)
а0 > 0, а1 > 0, а2 > 0, а3 > 0, а4 > 0,
а3 (а1 а3 - а0 а1)- а12 а4 > 0.
Система находится на границе устойчивости, если Δn = 0, а все предыдущие определители положительны. Это возможно при аn = 0 (апериодическая граница устойчивости) или при Δn-1 = 0 (колебательная граница устойчивости).
Если при проверке устойчивости оказалось, что система неустойчива, необходимо найти критический коэффициент усиления системы, при котором система будет на границе устойчивости. Критический коэффициент находят из уравнения Δ n-1 = 0.
4.3 Проверка устойчивости по критерию Михайлова
Для оценки устойчивости по критерию Михайлова необходимо построить кривую, которую описывает конец вектора D(jω) на комплексной плоскости при изменении частоты ω от 0до ∞, называемую годографом Михайлова
Вектор D(jω) получают из характеристического полинома замкнутой системы (9) при подстановке р = jω:
D(jω) = а0 (jω) n + a1 (jω) n-1 +a2(jω) n-2 ... +a n-1 (jω) +an. (12)
Выражение (12) представляют в виде
D(jω)=Х(ω) + jY(ω),
где Х(ω) и Y(ω), – вещественная и мнимая части D(jω) соответственно:
Х(ω) = an - an-2 ω2 + an-4 ω4 - . . . ;
Y(ω) = ω ( an-1 - an-3 ω2+ an-5 ω4- . . .) . (13)
Задавая значения ω от 0 до ∞, вычисляют Х(ω) и Y(ω). Расчет оформляют в виде таблицы 1
Таблица 1 –Координаты годографа Михайлова
ω |
0 |
0,1 |
1 |
2 |
3 |
4 |
5 |
. . . |
∞ |
Х(ω) |
|
|
|
|
|
|
|
|
|
Y(ω) |
|
|
|
|
|
|
|
|
|
По данным таблицы 1 строят годограф Михайлова.
Для устойчивости системы необходимо, чтобы годограф Михайлова обошел в положительном направлении (против часовой стрелки) последовательно n квадрантов, нигде не обращаясь в нуль. Если это условие не выполняется, система не устойчива. Если годограф проходит через начало координат, система на границе устойчивости.
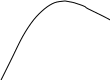
Приблизительный вид годографа Михайлова для устойчивых систем первого – четвертого порядков показан на рисунке 5.
Y(ω)
n=2 n=1
ω=0
Х(ω)
n=3
n=4
Рисунок 5 - Годографы Михайлова устойчивых систем