3.6 Основная часть

Основная часть содержит следующие разделы:

3.6.1 Анализ линейной системы автоматического регулирования.

3.6.2 Синтез линейной системы автоматического регулирования по заданным показателям качества.

3.6.3 Расчет переходного процесса скорректированной системы.

3.6.4 Выбор схемы и расчет параметров корректирующего устройства.

3.6.5 Анализ линейной системы автоматического регулирования включает следующие подразделы:

-преобразование структурной схемы и определение

передаточных функций системы;

- исследование системы на устойчивость по критерию Гурвица;

- исследование устойчивости системы по критерию Михайлова;

- исследование устойчивости системы по критерию Найквиста;

- определение устойчивости системы по логарифмическим частотным характеристикам;

-оценка точности системы в установившемся режиме.

3.6.6 Синтез линейной системы автоматического регулирования по логарифмическим частотным характеристикам включает подразделы:

- построение ЛАЧХ исходной системы;

- построение желаемой ЛАЧХ;

- проверка запаса устойчивости по фазе скорректированной системы;

- построение ЛАЧХ последовательного корректирующего устройства.

3.6.7 Расчет переходного процесса скорректированной системы содержит:

-определение передаточной функции замкнутой скорректированной системы;

- расчет вещественной характеристики замкнутой системы;

- расчет переходного процесса методом трапеций;

- оценка качества переходного процесса.

3.6.8 Выбор схемы и расчет параметров корректирующего устройства включает:

- определение передаточной функции корректирующего устройства;

- обоснование выбора схемы корректирующего устройства;

- принципиальную схему корректирующего устройства, наиболее точно реализующего требуемую передаточную функцию;

-расчет параметров корректирующего устройства.

3.7 Заключение

3.7.1 Заключение должно содержать выводы, сделанные на основании выполненной работы. В нем дается оценка полученных результатов.

3.8 Список использованных источников

3.8.1 Список использованных источников должен содержать перечень источников, ссылка на которые имеется в тексте. Сведения об источниках необходимо давать в соответствии с ГОСТ 7.1-84, СТП 3.4.204-01.

4 Методические указания к проектированию

4.1 Преобразование структурной схемы

Структурную схему любой сложности можно привести к одноконтурной (рисунок 1) с помощью последовательных преобразований.

Для преобразования структурной схемы прежде всего необходимо установить, какие имеются типовые соединения звеньев (последовательные, параллельные, встречно-параллельные). Каждое типовое соединение звеньев следует заменить эквивалентным звеном в соответствии с правилами структурных преобразований (Приложение Д).

f

W₀(p)

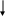
g

W₁(p)

W₂(p)

g х

y

– y

W₀(p)

Рисунок 1 - Одноконтурная структурная схема АСР

На рисунке 1 приняты следующие обозначения:

g - задающее воздействие;

f – возмущающее воздействие;

х – выходной сигнал (регулируемый параметр);

y – выходной параметр разомкнутой АСР, приведенный к виду, удобному для сравнения с g (сигнал обратной связи);

е –отклонение (рассогласование, ошибка), е(t)= g(t)- y_о(t);

W₁(p), W₂(p) – передаточные функции элементов прямой цепи;

W_о(p) – передаточная функция цепи обратной связи.

При определении передаточной функции замкнутой АСР по задающему воздействию относительно выходной величины (по входу g и выходу х) при условии f=0 исходную структурную схему (рисунок 1) представляем в виде, приведенном на рисунке 2.

g

W₁(p)

W₂(p)

е х

W₀(p)

y (t)

Рисунок 2 – Структурная схема АСР при управлении по задающему воздействию

Передаточная функция по определению представляет отношение изображения по Лапласу выходной величины Х(p) к изображению входной величины G(p) и выражается формулой

Х(p) W_П(p)

W_{х g} (p) = —— = ———— , (1) G(p) 1 + W(p)

где W_П(p) = W₁(p) * W₂(p) - передаточная функция прямой цепи;

W(p) - передаточная функция разомкнутой системы,

определяется как произведение всех последовательно соединенных звеньев, входящих в замкнутый контур:

W(p)= W₁(p)*W₂(p)*W₀(p). (2)

В случае единичной обратной связи W₀(p) =1 передаточная функция замкнутой системы

W(p)

W_{х g} (p) = ———— , (3) 1 + W(p)

а передаточная функция разомкнутой цепи

W(p)= W₁(p)*W₂(p). (4)

При определении передаточной функции по возмущающему воздействию полагают задающее воздействие равным нулю g = 0, тогда структурную схему можно преобразовать к виду, приведенному на

рисунке 3.

f

W₂(p)

W₃(p)

х

-

W₀(p)

W₁(p)

Рисунок 3- Структурная схема АСР по возмущающему воздействию

Далее, используя правило 7 переноса сумматора через звено (Приложение Д), получим эквивалентную структурную схему (рисунок 4).

f

W₃(p)

W₂(p)

х

-

W₀(p)

W₁(p)

W₄(p)

Рисунок 4 – Эквивалентная структурная схема АСР по возмущающему воздействию

Передаточная функция W₄(p)=1/ W₃(p).

Передаточная функция замкнутой системы по возмущающему воздействию относительно выходной величины х (по входу f и выходу х) в соответствии с (1) определяется выражением

Х(р) W₃(p)W₂(p)

W _хf (p) = —— = —————————————— = F(p) 1+W₁(p)W₂(p)W₃(p)W₀(p)W₄(p)

W₃(p)W₂(p) W_П(p)

= = , (5)

1+W₁(p) W₂(p) W₀(p) 1+W (p)

где W_П(p) = W₃(p)W₂(p) –передаточная функция прямой цепи;

W (p) = W₁(p) W₂(p) W₀(p) – передаточная функция разомкнутой системы.

Передаточная функция по ошибке для задающего воздействия

Е(р) 1

W_еg (p) = = . (6)

G(p) 1+W (p)

Передаточная функция по ошибке по возмущающему воздействию

F(р) W₃(p)W₂(p)

W_еf (p) = = - ————— . (7)

G(p) 1+W (p)

После подстановки передаточных функций звеньев выражения для передаточных функций системы приобретают вид сложных дробей, числитель и знаменатель которых представляют дробную структуру. Для дальнейших вычислений необходимо провести преобразования, в результате которых выражения (1-7) принимают вид простых дробей вида:

b₀ p^m+b₁p^m-1+b₂p^m-2+ … +b_m

W(p) = ————————————— , (8) а₀ рⁿ+a₁p^n-1+a₂p^n-2+ ... +a_n

где а_{0 ,} a_{1 ,}a₂ ... a_n , b_{0 ,} b_1, b₂ … b_m – постоянные коэффициенты, зависящие от параметров звеньев, составляющих структурную схему (постоянных времени Т и коэффициентов усиления К). Сначала коэффициенты передаточной функции системы необходимо записать в общем виде, выразив их через параметры звеньев, а затем подставить численные значения.

Характеристическое уравнение замкнутой АСР получается путем выделения знаменателя ее передаточной функции после преобразования ее к виду (8) и приравнивания его к нулю

а₀ рⁿ+a₁p^n-1+a₂p^n-2+ ... +a_n=0. (9)