5. Характеристика технологических процессов

Рассмотрим технологический процесс изготовления шоколада.

Технологический процесс - это упорядоченная последовательность взаимосвязанных действий, выполняющихся с момента возникновения исходных данных до получения требуемого результата.

Технологический процесс производства шоколада представляет сложно -линейную структуру производства.

INCLUDEPICTURE "http://uslugi-pomola.ru/img/000_wella_stat_plod_shema2.jpg" \* MERGEFORMATINET

рис 2. Сложно-линейная структура производства шоколада

1. При первичной подготовке какао бобов к обработке необходимо стремиться, прежде всего, к получению шоколада наивысшего качества. Качество шоколада будет тем выше, чем лучше будет измельчена какао-крупка. Крупные фракции крупки используются для получения плиточного шоколада, а менее ценные мелкие – для приготовления начинок, конфетных масс и шоколадной глазури.

2. В результате размола какао-крупки получается какао тертое, которое при температуре свыше + 40о С представляет собой густую сметанообразную жидкость, состоящую их какао-масла и измельченных клеточных стенок какао-бобов. Чем лучше будет измельчена твердая фаза какао тертого, тем мельче будут частицы, ложащиеся на рецепторы, тем более полным и тонким будет представляться человеку вкус шоколада.

3. Приготовление шоколадных масс это тонкодисперсная смесь,  для приготовления которой компоненты добавляют друг к другу в строго определенной последовательности: какао тертое, сахарная пудра, добавки, какао-масло.

4. После получения шоколадной массы следует механический процесс вальцевания, где твердые частицы еще больше измельчаются и шоколадная масса из пластической становится сыпучей и комкающейся. Затем полученную массу разжижают добавлением какао масла или пальмового масла. На этом этапе в массу попадают ароматизаторы, спирт, вина и тому подобные компоненты.

5. Шоколадные массы после разводки подвергаются коншированию - это весьма тонкая операция, от которой решающим образом зависит качество шоколада. Внешне конширование представляет собой непрерывное и очень длительное перемешивание подогретой шоколадной массы, которая постоянно соприкасается с воздухом.

6. Для получения качественного шоколада -  приготовленную шоколадную массу с температурой +40-45^оС сначала  быстро охлаждают до +33 ^оС, выдерживают минут 30-40  при этой температуре интенсивно перемешивания. За это время в шоколадной массе равномерно образуются центры кристаллизации  только бета-формы. Другие формы кристаллизации какао-масла (шоколад низкого качества)  при такой температуре не образуются.

7. Последние стадии процесса производства шоколада – завертывание и упаковывание. В соответствии с действующими в мире стандартами, шоколад, выпускаемый в плитках завертывают в алюминиевую фольгу и художественную этикетку. Обычно на современных фабриках эти процессы выполняются на поточных линиях механическим путем.

1.6 Характеристика тоу как объекта управления.

Главной целью данного объекта управления является обеспечение непрерывного качественного производства шоколада.

По способу организации такой процесс производства является дискретно-непрерывным, что в свою очередь, в сочетании с постоянным потребительским спросом, говорит о непрерывности и способствует автоматизации его управления.

Обычно разные сорта шоколада производят на разных линиях. Это дает возможность не изменять заданные единожды входные параметры сырья, при условии соответствия выходной продукции признанным нормам и требованиям.

Если проанализировать процесс производства шоколада как объект автоматического управления, то можно выделить следующие

Производство шоколада имеет три группы показателей: входные воздействия, условия протекания технологического процесса, выходные показатели.

К входным показателям относят: вид и сорт используемых какао бобов, качество какао бобов, температура сырья перед измельчением.

К условиям протекания технологического процесса относят: размер крупки и качество какао масла и т.д.

К выходным показателям относят: внешний вид, целостность, качество и температуру плавления на языке.

Из числа выходных показателей можно выделяют управляющие и возмущающие воздействия.

Управляющие воздействия можно изменять соответственно для изменения хода процесса. Например изменение времени конширования шоколада или измельчения крупки.

Возмущающие воздействия можно только учитывать. Они могут проявить себя в тот или иной момент. Например кратковременный перепад напряжения может вызвать кратковременную остановку работы оборудования, что не сильно скажется на качестве продукции. А вот отключение света на продолжительное время сильно отразится на процессе производства.

2. Анализ временного ряда по данным о работе ТОУ.

Цель данной работы: анализ временного ряда построенного в виде таблицы 1 и графика (см. рисунок 1) на основании данных промышленной эксплуатации действующего объекта – дуговой печи. Таблица составлена на основании данных химического анализа кремния на выпуске. Задачей данной работы является анализ показателей хода технологического процесса с использованием фильтров на примере определения нарушений процессов в виде тенденции.

Таблица 1. – Содержание кремния в песке на выпуске

t	Si %	t	Si %
1	0,660	26	0,380
2	0,370	27	0,500
3	0,570	28	0,460
4	0,560	29	0,600
5	0,580	30	0,580
6	0,420	31	0,720
7	0,450	32	0,670
8	0,470	33	0,870
9	0,460	34	0,670
10	1,100	35	0,560
11	0,660	36	0,690
12	0,760	37	0,700
13	0,570	38	0,690
14	0,590	39	0,560
15	0,800	40	0,590
16	0,810	41	0,690
17	0,690	42	0,670
18	0,710	43	0,580
19	0,660	44	0,780
20	0,740	45	0,770
21	0,620	46	0,820
22	0,510	47	0,470
23	0,460	48	0,420
24	0,620	49	0,460
25	0,450	50	0,440

Р исунок 1. – Содержание кремния в песке на выпуске

Алгоритм решения задачи.

Анализ временного ряда включает следующие этапы:

1. Краткое описание характерных особенностей ряда (визуальный анализ).

2. Выявление аномальных значений уровней ряда.

3. Сглаживание временного ряда.

4. Определение наличия тренда.

5. Формирование набора трендовых моделей.

6. Оценка адекватности и точности трендовых моделей.

1. Визуальный анализ.

На графике «Содержание кремния в песке на выпуске» изображенном на рисунке 1 можно увидеть отсутствие закономерности значений временного ряда. Значения рассеяны в диапазоне от 0,35% до 0,9%. Также на графике можно увидеть аномальное значение, которое равное 1,1% кремния при t=10.

2. Выявление аномальных значений уровней ряда.

Под аномальным уровнем понимается отдельное значение уровня временного ряда, которое не отвечает потенциальным возможностям исследуемой экономической системы и которое, оставаясь в качестве уровня ряда, оказывает существенное влияние на значения основных характеристик временного ряда, в том числе на соответствующую трендовую модель. Причинами аномальных наблюдений могут быть ошибки технического порядка, или ошибки первого рода: ошибки при агрегировании и дезагрегировании показателей, при передаче информации и другие технические причины. Ошибки первого рода подлежат выявлению и устранению. Кроме того, аномальные уровни во временных рядах могут возникать из-за воздействия факторов, имеющих объективный характер, но проявляющихся эпизодически, очень редко — ошибки второго рода; они устранению не подлежат.

Для выявления аномальных уровней временных рядов используется метод Ирвина. Он рассчитан для статических совокупностей, результаты которых приведены в таблице 2.

Таблица 2. – Содержание кремния в песке на выпуске (Аномальные значения уровней ряда – метод Ирвина).

t	Si	л(И)	t	Si	л(И)
1	0,660		26	0,380	0,484185397
2	0,370	2,005911423	27	0,500	0,830032227
3	0,570	1,383386976	28	0,460	0,27667734
4	0,560	0,069169283	29	0,600	0,968371001
5	0,580	0,138338566	30	0,580	0,138338981
6	0,420	1,106709567	31	0,720	0,968371277
7	0,450	0,207508057	32	0,670	0,34584683
Продолжение таблицы 2
8	0,470	0,138338774	33	0,870	1,383386907
9	0,460	0,069169283	34	0,670	1,383386907
10	1,100	4,426838475	35	0,560	0,760863013
11	0,660	3,043451292	36	0,690	0,899201579
12	0,760	0,691693246	37	0,700	0,069169283
13	0,570	1,314217693	38	0,690	0,069169283
14	0,590	0,138338566	39	0,560	0,899201579
15	0,800	1,452556674	40	0,590	0,207507849
16	0,810	0,069169283	41	0,690	0,69169373
17	0,690	0,830032227	42	0,670	0,138338566
18	0,710	0,138338566	43	0,580	0,622524447
19	0,660	0,345846415	44	0,780	1,383386976
20	0,740	0,55335468	45	0,770	0,069169283
21	0,620	0,830032296	46	0,820	0,34584683
22	0,510	0,760862944	47	0,470	2,42092726
23	0,460	0,345846623	48	0,420	0,34584683
24	0,620	1,106709567	49	0,460	0,276677547
25	0,450	1,175879058	50	0,440	0,138338774

В результате этого условия были определены аномальные значения ряда данных. В таблице 2 представлен результат определения аномальных значений ряда.

Также проверка производилась по методу трех сигм (3σ), суть которого в том, что случайная величина отклонится от своего математического ожидания на большую величину, чем утроенное среднее квадратичное отклонение, практически равна нулю. Правило справедливо только для случайных величин, распределенных по нормальному закону. С вероятностью 0,95 значение временного ряда должно попадать в интервал [ŷ-3σ; ŷ+3σ]. Если значение попадает в данный интервал, то речь идет о нормальном распределении случайной величины и не аномальном значении ряда, если же значение выходит за границы доверительного интервала, то значение – аномальное.

Вследствие этого условия были определены аномальные значения ряда данных. В таблице 3 представлен результат определения аномальных значений ряда.

Таблица 3. – Содержание кремния в песке на выпуске (Аномальные значения уровней ряда – метод трёх сигм).

t	Si	y	by	t	Si	y	by
1	0,660	0,0474	0,3511347	26	0,380	0,2326	0,3511347
2	0,370	0,2426	0,3511347	27	0,500	0,1126	0,3511347
3	0,570	0,0426	0,3511347	28	0,460	0,1526	0,3511347
Продолжение таблицы 3
4	0,560	0,0526	0,3511347	29	0,600	0,0126	0,3511347
5	0,580	0,0326	0,3511347	30	0,580	0,0326	0,3511347
6	0,420	0,1926	0,3511347	31	0,720	0,1074	0,3511347
7	0,450	0,1626	0,3511347	32	0,670	0,0574	0,3511347
8	0,470	0,1426	0,3511347	33	0,870	0,2574	0,3511347
9	0,460	0,1526	0,3511347	34	0,670	0,0574	0,3511347
10	1,100	0,4874	0,3511347	35	0,560	0,0526	0,3511347
11	0,660	0,0474	0,3511347	36	0,690	0,0774	0,3511347
12	0,760	0,1474	0,3511347	37	0,700	0,0874	0,3511347
13	0,570	0,0426	0,3511347	38	0,690	0,0774	0,3511347
14	0,590	0,0226	0,3511347	39	0,560	0,0526	0,3511347
15	0,800	0,1874	0,3511347	40	0,590	0,0226	0,3511347
16	0,810	0,1974	0,3511347	41	0,690	0,0774	0,3511347
17	0,690	0,0774	0,3511347	42	0,670	0,0574	0,3511347
18	0,710	0,0974	0,3511347	43	0,580	0,0326	0,3511347
19	0,660	0,0474	0,3511347	44	0,780	0,1674	0,3511347
20	0,740	0,1274	0,3511347	45	0,770	0,1574	0,3511347
21	0,620	0,0074	0,3511347	46	0,820	0,2074	0,3511347
22	0,510	0,1026	0,3511347	47	0,470	0,1426	0,3511347
23	0,460	0,1526	0,3511347	48	0,420	0,1926	0,3511347
24	0,620	0,0074	0,3511347	49	0,460	0,1526	0,3511347
25	0,450	0,1626	0,3511347	50	0,440	0,1726	0,3511347

3. Сглаживание временного ряда.

Уровни временных рядов часто колеблются. При этом тенденция развития явления во времени скрыта случайными отклонениями уровней в ту или иную сторону. Возникает потребность их разделения на несколько составляющих с различными темпами изменения, и тогда говорят о применении фильтров, реализуемых аппаратурными и алгометрическими средствами. Если есть основания принять математическую модель рядов данных в виде суммы медленноменяющихся полезных сигналов и относительно быстроменяющихся помех, то первичная обработка числовых данных может быть успешно сведена к их преобразованию в так называемых сглаживающих фильтрах. К настоящему времени разработано множество таких фильтров, отличающихся заложенными в них предпосылками, сложностью и точностью.

В работе сглаживание применялся метод скользящей средней по трём и пяти точкам в данной работе с использованием функции «срзнач» мастера функций Microsoft Excel. Результаты приведены в таблице 4 и на рисунках 2, 3.

Таблица 4. – Содержание кремния в песке на выпуске (скользящее среднее).

t	Si	Si(3)	Si(5)	t	Si	Si(3)	Si(5)
1	0,660			26	0,380	0,443	0,482
2	0,370	0,533		27	0,500	0,447	0,478
3	0,570	0,500	0,548	28	0,460	0,520	0,504
4	0,560	0,570	0,500	29	0,600	0,547	0,572
5	0,580	0,520	0,516	30	0,580	0,633	0,606
6	0,420	0,483	0,496	31	0,720	0,657	0,688
7	0,450	0,447	0,476	32	0,670	0,753	0,702
8	0,470	0,460	0,580	33	0,870	0,737	0,698
9	0,460	0,677	0,628	34	0,670	0,700	0,692
10	1,100	0,740	0,690	35	0,560	0,640	0,698
11	0,660	0,840	0,710	36	0,690	0,650	0,662
12	0,760	0,663	0,736	37	0,700	0,693	0,640
13	0,570	0,640	0,676	38	0,690	0,650	0,646
14	0,590	0,653	0,706	39	0,560	0,613	0,646
15	0,800	0,733	0,692	40	0,590	0,613	0,640
16	0,810	0,767	0,720	41	0,690	0,650	0,618
17	0,690	0,737	0,734	42	0,670	0,647	0,662
18	0,710	0,687	0,722	43	0,580	0,677	0,698
19	0,660	0,703	0,684	44	0,780	0,710	0,724
20	0,740	0,673	0,648	45	0,770	0,790	0,684
21	0,620	0,623	0,598	46	0,820	0,687	0,652
22	0,510	0,530	0,590	47	0,470	0,570	0,588
23	0,460	0,530	0,532	48	0,420	0,450	0,522
24	0,620	0,510	0,484	49	0,460	0,440
25	0,450	0,483	0,482	50	0,440

Как видно из графиков (см. рисунок 2, 3) сглаживание подтверждает предположение об отсутствии предположении закономерной изменяющейся составляющей в данном временном ряду. Графическое изображение сглаженного ряда напоминает прямую линию, что объясняется взаимопогашением случайных колебаний в среднем уровне и даёт представление поведения прямого ряда. По графикам видно, что ряд, полученный по пяти точкам, имеет более сглаженный вид.

Рисунок 2. – Содержание кремния в песке на выпуске (сглаживание временного ряда по трём точкам).

Рисунок 3. – Содержание кремния в песке на выпуске (сглаживание временного ряда по пяти точкам).

Помимо скользящей средней можно также использовать медиану значении, которые попали в окно.

В работе сглаживание осуществляется методом скользящей средней по 3 и 5 точкам. Было использована функция «медиана» из мастера функций Microsoft Excel. Ее результаты приведены в таблице 5 и на рисунках 4 и 5.

Таблица 5. Содержание кремния в песке на выпуске (медианное сглаживание).

t	Si	Si(3)	Si(5)	t	Si	Si(3)	Si(5)
1	0,660			26	0,380	0,450	0,460
2	0,370	0,570		27	0,500	0,460	0,460
3	0,570	0,560	0,570	28	0,460	0,500	0,500
4	0,560	0,570	0,560	29	0,600	0,580	0,580
5	0,580	0,560	0,560	30	0,580	0,600	0,600
6	0,420	0,450	0,470	31	0,720	0,670	0,670
7	0,450	0,450	0,460	32	0,670	0,720	0,670
8	0,470	0,460	0,460	33	0,870	0,670	0,670
9	0,460	0,470	0,470	34	0,670	0,670	0,670
10	1,100	0,660	0,660	35	0,560	0,670	0,690
11	0,660	0,760	0,660	36	0,690	0,690	0,690
12	0,760	0,660	0,660	37	0,700	0,690	0,690
13	0,570	0,590	0,660	38	0,690	0,690	0,690
14	0,590	0,590	0,760	39	0,560	0,590	0,690
15	0,800	0,800	0,690	40	0,590	0,590	0,670
16	0,810	0,800	0,710	41	0,690	0,670	0,590
17	0,690	0,710	0,710	42	0,670	0,670	0,670
18	0,710	0,690	0,710	43	0,580	0,670	0,690
19	0,660	0,710	0,690	44	0,780	0,770	0,770
20	0,740	0,660	0,660	45	0,770	0,780	0,770
21	0,620	0,620	0,620	46	0,820	0,770	0,770
22	0,510	0,510	0,620	47	0,470	0,470	0,470
23	0,460	0,510	0,510	48	0,420	0,460	0,460
24	0,620	0,460	0,460	49	0,460	0,440
25	0,450	0,450	0,460	50	0,440

И з этого можно сделать вывод: медианное сглаживание показывает более точное отражение тенденции изменения ряда.

Рисунок 4. Содержание кремния в песке на выпуске (медианное сглаживание по трём точкам).

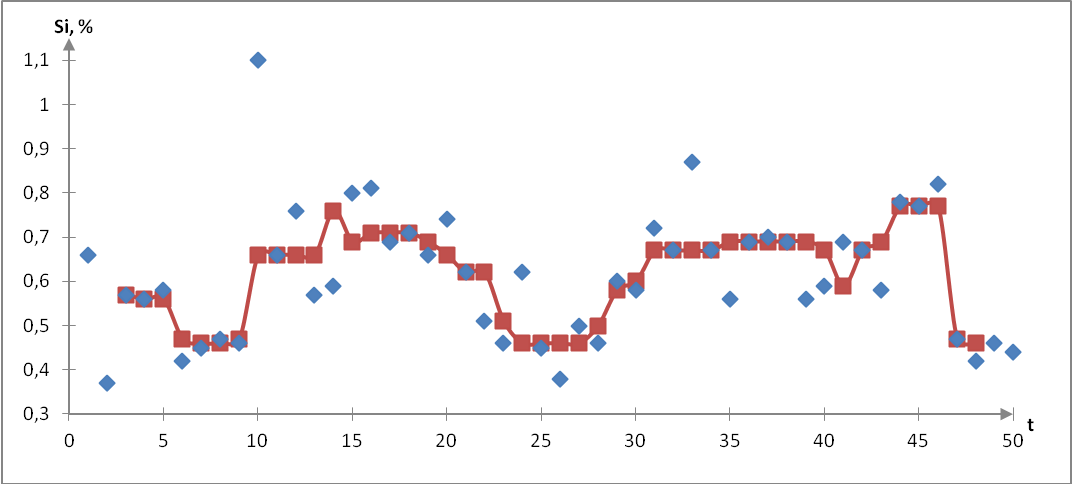
Рисунок 5. Содержание кремния в песке на выпуске (медианное сглаживание по пяти точкам).

4. Определение наличия тренда.

Важную роль в решении задач выявления и оценивания сезонной, трендовой, нерегулярной и циклической составляющих играет начальный этап анализа. На нем:

1. устанавливается факт наличия или отсутствия неслучайной и зависящей от времени (t) составляющей;

2. определяется оценка (аппроксимация) для неизвестной составляющей. Другими словами, решается задача (элиминирования) исключения случайных остатков (сглаживания) анализируемого временного ряда y(t);

Метод критерий серий и метод восходящей и нисходящей, применяется для определения наличия тренда в исходном временном ряду.

С целью проверки гипотезы о неизменности среднего значения временного ряда (случайности ряда) рассматривается критерий серий, основанный на медиане.

Значение временного ряда сопоставляется с выборочной медианой, и если x(t) > , то для соответствующего наблюдения член последовательности, образующего серии, принимает знак «+», если x(t) < , то – знак «-» (см. таблицу 6).

В методе критерий серий, основанном на медиане выборки, для того чтобы не была отвергнута гипотеза о случайности исходного ряда (об отсутствии систематической составляющей), должны выполняться следующие неравенства (для 5% уровня значимости):

₍₁₎

где:

• n – длина временного ряда;

• ν(n) – число серий;

• τ_max(n) – число подряд идущих плюсов или минусов в самой длинной серии;

• [ ] - целая часть числа.

Если хотя бы одно из неравенств нарушается, то гипотеза об отсутствии тренда отвергается с вероятностью ошибки α, заключенной между 0,05 и 0,0975. Следовательно, подтверждается наличие зависящей от времени неслучайной составляющей исследуемого ряда

В работе метод критерий серий осуществляется при помощи использования стандартных формул из математического и логического модулей. Результаты приведены в таблице 6.

Если хотя бы одно из неравенств (1) нарушается, то гипотеза об отсутствии тренда отвергается, в данном случае нарушены оба неравенства. Из этого следует вывод о наличии тренда.

t	Si	Медиана		t	Si	Медиана
1	0,660	0,595	+	26	0,380	0,595	-
2	0,370	0,595	-	27	0,500	0,595	-
3	0,570	0,595	-	28	0,460	0,595	-
4	0,560	0,595	-	29	0,600	0,595	+
5	0,580	0,595	-	30	0,580	0,595	-
6	0,420	0,595	-	31	0,720	0,595	+
7	0,450	0,595	-	32	0,670	0,595	+
8	0,470	0,595	-	33	0,870	0,595	+
9	0,460	0,595	-	34	0,670	0,595	+
10	1,100	0,595	+	35	0,560	0,595	-
11	0,660	0,595	+	36	0,690	0,595	+
12	0,760	0,595	+	37	0,700	0,595	+
13	0,570	0,595	-	38	0,690	0,595	+
14	0,590	0,595	-	39	0,560	0,595	-
15	0,800	0,595	+	40	0,590	0,595	-
16	0,810	0,595	+	41	0,690	0,595	+
17	0,690	0,595	+	42	0,670	0,595	+
18	0,710	0,595	+	43	0,580	0,595	-
19	0,660	0,595	+	44	0,780	0,595	+
20	0,740	0,595	+	45	0,770	0,595	+
21	0,620	0,595	+	46	0,820	0,595	+
22	0,510	0,595	-	47	0,470	0,595	-
23	0,460	0,595	-	48	0,420	0,595	-
24	0,620	0,595	+	49	0,460	0,595	-
25	0,450	0,595	-	50	0,440	0,595	-

Таблица 6. Содержание кремния в песке на выпуске (метод критерий серий)

Проверка гипотезы по «восходящей» и «нисходящей» серий основывается на том, что при условии случайности ряда (при отсутствии систематической составляющей) протяженность самой длинной серии не должна быть слишком большой, а общее число серий – слишком маленьким.

Каждое значение временного ряда сравнивается с предыдущим, и, если x_t > x_t-1, то для соответствующего наблюдения член последовательности, образующего серии, принимает знак«+», если x_t < x_t-1, то – знак «-» (см. таблицу 7).

Критерий «восходящих» и «нисходящих» серий устанавливается исходя из системы неравенств.

₍₂₎

где:

• n – длина временного ряда;

• ν(n) – число серий;

• τ_max(n) – число подряд идущих плюсов или минусов в самой длинной серии.

Следует отметить, что τ0 принимает значения в зависимости от n т.е.: если n ≤26, то τ₀ = 5; если 26< n ≤ 153, то τ₀ = 6; и если 153<n≤ 1170, то τ₀ = 7. Если хотя бы одно из неравенств окажется нарушенным, то гипотезу об отсутствии тренда следует отвергнуть, т.е. признать, что в анализируемом временном ряду присутствует неслучайная, зависящая от времени t компонента.

В работе метод восходящей и нисходящей осуществляется при помощи использования стандартных формул из математического и логического модулей. Результаты приведены в таблице 7.

Если хотя бы одно из неравенств (2) нарушается, то гипотеза об отсутствии тренда отвергается, в данном случае нарушено одно неравенство. Из этого следует вывод о наличии тренда

Таблица 7. Содержание кремния в чугуне на выходе(метод восходящей и нисходящей)

t	Si
1	0,660		26	0,380	-
2	0,370	-	27	0,500	+
3	0,570	+	28	0,460	-
4	0,560	-	29	0,600	+
5	0,580	+	30	0,580	-
6	0,420	-	31	0,720	+
7	0,450	+	32	0,670	-
8	0,470	+	33	0,870	+
9	0,460	-	34	0,670	-
10	1,100	+	35	0,560	-
11	0,660	-	36	0,690	+
12	0,760	+	37	0,700	+
13	0,570	-	38	0,690	-
14	0,590	+	39	0,560	-
15	0,800	+	40	0,590	+
16	0,810	+	41	0,690	+
17	0,690	-	42	0,670	-
18	0,710	+	43	0,580	-
19	0,660	-	44	0,780	+
20	0,740	+	45	0,770	-
Продолжение таблицы 7
21	0,620	-	46	0,820	+
22	0,510	-	47	0,470	-
23	0,460	-	48	0,420	-
24	0,620	+	49	0,460	+
25	0,450	-	50	0,440	-

2.5 Формирование набора трендовых моделей.

Набор моделей формируется на основе формализованных статистических процедур (исследование приростов уровней), интуитивных приемов (таких, например, как анализ графика динамики ряда), знания специфики используемых функций, их возможности отразить те или иные нюансы развития. Вспомогательную роль при выборе аналитической функции также играют механические приемы сглаживания (метод скользящего среднего, медианное и экспоненциальное сглаживание). Частично устраняя случайные колебания, они помогают более точно определить тренд и выбрать адекватную модель для аналитического выравнивания. При этом предпочтение отдается наиболее простым, содержательно интерпретируемым моделям, решаемым программным путем на ЭВМ с проведением вычислений по всем доступным моделям и методам.

В работе набор трендовых моделей рассчитан при помощи добавлении линии тренда на график. Результаты приведены в таблице 8 и на рисунках 4,5,6.

Таблица 8. Набор трендовых моделей

№	Вид зависимости	Уравнение зависимости
1	Линейная	y^ = 0,0005*Si + 0,601

Р исунок 6. Набор трендовых моделей (линейная).

Просмотрев и проанализировав графики построенных трендовых моделей, можно сказать, что адекватных моделей не найдено. Но для приведения примеров проверки точности и адекватности была выбрана линейная модель.

2.6 Оценка адекватности и точности трендовых моделей.

Основа для построения прогноза по лучшей модели, выбранной по критериям адекватности и точности – это информация, содержащаяся в рабочей базе моделей. При этом адекватность моделей оценивается по свойствам остаточной компоненты (расхождениям, рассчитанным по модели уровней и фактических наблюдений), а точность модели - по степени близости расчетных данных к фактическим.

Проверка случайности колебаний уровней остаточной последовательности означает проверку гипотезы о правильности выбора вида тренда. Для исследования случайности отклонений от тренда необходимо располагать набором разностей (Формула 5)

(t =1 , 2, . . ., n) (5)

Характер этих отклонений изучается с помощью ряда непараметрических критериев. Критерий пиков (поворотных точек) - является одним из таких критериев. Уровень последовательности _t считается максимумом, если он больше двух рядом стоящих уровней, т.е. _{t -1} < _t >_t+1, и минимумом, если он меньше обоих соседних уровней, т.е. _{t -1} > _t <_t+1. В обоих случаях _t считается поворотной точкой; общее число поворотных точек для остаточной последовательности _t обозначим через р.

Критерием случайности с уровнем значимости =0,05 является выполнение неравенства (6).

(6)

где квадратные скобки означают целую часть числа, это неравенство выполняется, 36 > 26 условие выполняется, трендовая модель считается неадекватной.

Проверка соответствия распределения случайной компоненты нормальному закону распределения может быть произведена по RS-критерию.

Этот критерий численно равен отношению размаха вариации случайной величины R= _max-_min к стандартному отклонению, вычисляемому по формуле 7.

(7)

σ=0,18

Вычисленное значение RS -критерия сравнивается с табличными значениями, которые равны 3,47 и 4,89, верхнее и нижнее соответственно. В данном случае рассчитанное значение не попадает в данный интервал, модель считается распределенной не по нормальному закону, т. е. не адекватной.

Проверка равенства математического ожидания случайной компоненты нулю, если она распределена по нормальному закону, осуществляется на основе t-критерия Стьюдента. Расчетное значение этого критерия задается формулой 8.

(8)

где — среднее арифметическое значение уровней остаточной последовательности _t;

_ — стандартное (среднеквадратическое) отклонение для этой последовательности.

Расчетное значение t = 4,22 больше табличного значения t=2,00 статистики Стьюдента с уровнем значимости 0,95 , гипотеза о равенстве нулю математического ожидания случайной последовательности принимается, модель не адекватна.

Проверка независимости значений уровней случайной компоненты, т.е. проверка отсутствия существенной автокорреляции в остаточной последовательности осуществляется через d-критерий Дарбина — Уотсона. Расчетное значение этого критерия определяется по формуле 9:

(9)

Расчетное значение критерия d =0,09 меньше нижнего табличного значения d₂ =1,35 то гипотеза о независимости уровней остаточной последовательности, т.е. об отсутствии в ней автокорреляции, отвергается, т.е. модель неадекватна.

Отсюда вывод, что модель является неадекватной по причине не выполнения всех критериев одновременно.

В качестве статистических показателей точности применяются следующие формулы:

• Среднеквадратичное отклонение (СКО). (Формула 10)

(10)

σ=1,02

• Средняя относительная ошибка аппроксимации (ошибка менее 5% свидетельствует об удовлетворительном уровне точности; ошибка в 10% и более считается большой). (Формула 11)

(11)

= 0,41%

• коэффициент сходимости (Формула 12).

(12)

ϕ² =-1,19

Коэффициент детерминации (трендовая модель адекватна изучаемому процессу и отражает тенденцию его развития во времени при значениях R², близких к 1). (Формула 13)

(13)

R² = 0,19

В приведенных формулах (7- 13): n — количество уровней ряда, k — число определяемых параметров модели, - оценка уровней ряда по модели, - среднее арифметическое значение уровней ряда.

Вывод: после проверки на точность и адекватность данной линейной модели временного ряда, определили, что она не адекватна и не точна.

Заключение

В курсовой работе «Анализ технологии производства шоколада как объекта автоматизации» изучен технологический процесс производства шоколада, характеристики сырья для изготовления шоколада и готовой продукции и описание основного оборудования данного производства.

За относительно коротки промежуток времени, технологически прорыв в области изготовления шоколада достиг очень больших высот. А именно:

• уменьшение затрат на производство;

• увеличение качества;

• увеличение вкуса и выбора;

• и т. д.

Современное производство шоколада.

Современная шоколадная фабрика представляет собой автоматизированную линию с электронным управлением, закрытую от любых внешних воздействий, техническое оснащение которой позволяет поддерживать заданные технологические параметры на разных этапах производства, что гарантирует выпуск высококачественной шоколадной продукции с длительным сроком годности без использования стабилизаторов и консервантов.

Её работа полностью контролируется компьютером: «Виртуальный мозг», в зависимости от типа производимой продукции выбирает одну из программ, хранящихся в его памяти, и сам осуществляет наблюдение за всеми процессами, следит за поддержанием наружного температурного режима и быстротой выполнения операций. В случае необходимости проводит проверку своей работы и вносит нужные коррективы.

Список использованных источников

1. Характеристика сырья и вспомогательных материалов [Электронный ресурс]. - http://baker-group.net/production-of-chocolate-and-cocoa/1431-characteristic-parts-cocoa-beans.html

2. Производство шоколада и шоколадных масс [Электронный ресурс]. - http://baker-group.net/products-and-technologies/569-preparation-of-chocolate-masses.html

3. Технология производства шоколада [Электронный ресурс]. - http://www.spartak.by/ru/press/publication/173

50