Лекция №3 Основные понятия теории погрешностей

Классификация погрешностей. Правила округления результатов измерений. Случайная и систематическая погрешности, промахи.

В результате проведения эксперимента всегда получается какое-либо число либо ряд чисел. Цель обработки результатов измерений – записать этот ряд чисел или число в виде, пригодном для непосредственного использования. Принципиальная трудность такой задачи состоит в том, что, согласно постулату теории измерений, мы никогда не получаем истинного значения измеряемой величины.

Степень близости результата измерения к истинному значению величины характеризуется погрешностью измерения.

Истинным называется значение ФВ, идеальным образом характеризующее свойство данного объекта как в количественном, так и в качественном отношении.

На практике это абстрактное понятие приходится заменять понятием «действительное значение».

Действительным называется значение ФВ, найденное экспериментально и настолько близкое к истинному, что в поставленной измерительной задаче оно может быть использовано вместо него.

Результат измерения представляет собой значение величины, полученное путем измерения.

Погрешность результата измерения – это отклонение результата измерения от истинного (или действительного) значения измеряемой величины.

Она указывает границы неопределенности значения измеряемой величины.

Близость к нулю погрешности результата измерения отражает точность результата измерений, которая является одной из характеристик качества измерения. Чем меньше погрешность измерения, тем больше его точность.

Погрешность средства измерений – разность между показанием СИ и истинным (действительным) значением измеряемой ФВ. Она характеризует точность средства измерений (характеристику качества СИ, отражающую близость его погрешности к нулю).

Понятия погрешности результата измерения и погрешности средства измерений во многом близки друг к другу и классифицируются по одинаковым признакам.

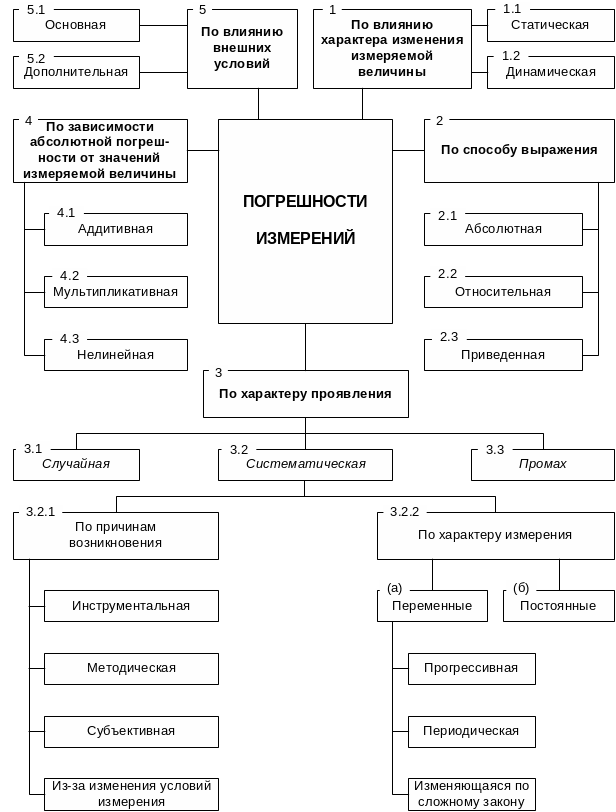
Рис. О-5 Классификация погрешностей измерений

1) В зависимости от влияния характера изменения измеряемых величин погрешности СИ делят на (1.1) статические и (1.2) динамические.

Статической называется погрешность результата измерений ФВ, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.

Динамической называется погрешность результата измерения изменяющейся по размеру ФВ.

2) По способу выражения различают (2.1) абсолютную, (2.2) относительную и (2.3) приведенную погрешности.

Абсолютная погрешность – погрешность измерения, выраженная в единицах измеряемой величины.

;

Относительная погрешность – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.

,

где Δ – абсолютная погрешность измерений; х – действительное или измеренное значение

Из этих отношений находят относительную погрешность в долях измеряемой величины или процентах.

Эта наглядная характеристика точности результата измерения не годится для нормирования погрешности СИ. В связи с этим для указания и нормирования погрешности СИ используется приведенная погрешность.

Приведенная погрешность средства измерений – это относительная погрешность, выраженная отношением абсолютной погрешности СИ к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона.

Условно принятое значение величины называют нормирующим значением. Часто за нормирующее значение принимают верхний предел измерений .

3) По характеру проявления погрешности делятся на (3.1) случайные, (3.2) систематические и (3.3) промахи (или грубые погрешности).

Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера ФВ, проведенных с одинаковой тщательностью в одних и тех же условиях. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения, однако их можно существенно уменьшить, увеличив число наблюдений.

Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики. Для получения результата, минимально отличающегося от истинного значения измеряемой величины, проводят многократные измерения требуемой величины с последующей математической обработкой экспериментальных данных.

Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же ФВ.

Их отличительный признак заключается в том, что они могут быть предсказаны, обнаружены и благодаря этому почти полностью устранены введением соответствующей поправки.

Грубая погрешность (промах) – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.

4) По зависимости абсолютной погрешности от значений измеряемой величины различают погрешности:

(4.1) аддитивные Δa, не зависящие от измеряемой величины;

(4.2) мультипликативные Δм, которые прямо пропорциональны измеряемой величине,

(4.3) нелинейные Δн, имеющие нелинейную зависимость от измеряемой величины.

Эти погрешности применяют в основном для описания метрологических характеристик СИ.

5) По влиянию внешних условий различают (5.1) основную и (5.2) дополнительную погрешности СИ.

Основная погрешность средства измерений – погрешность СИ, применяемого в нормальных условиях.

Дополнительная погрешность средства измерений – составляющая погрешности СИ, возникающая дополнительно к основной погрешности, вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений.