Классификация физических величин
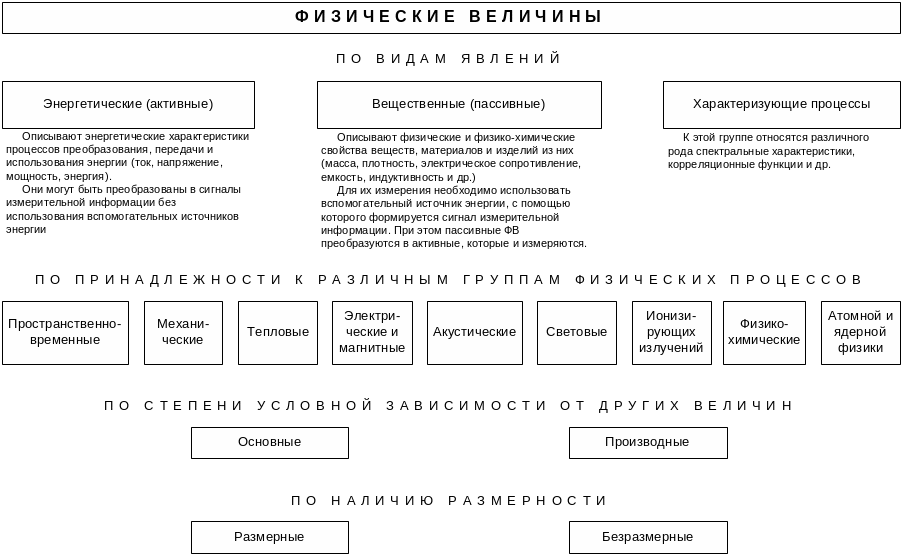
Рассмотрим КАЧЕСТВЕННЫЕ и КОЛИЧЕСТВЕННЫЕ характеристики измеряемых величин
Качественная характеристика измеряемых величин
Формализованным отражением качественного различия между измеряемыми физическими величинами служит их размерность. Размерность обозначается символом dim (dimension).
Размерность физической величины dim Q – выражение в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях и отражающее связь данной ФВ с ФВ, принятыми в данной системе за основные с коэффициентом пропорциональности, равным 1:
dim Q = LαMβTγ…,
где
L, M, T, … – размерности соответствующих основных ФВ;
α, β, γ, … – показатели размерности. Каждый из показателей размерности может быть положительным или отрицательным, целым или дробным числом, нулём. Если все показатели размерности равны нулю, то такую величину называют безразмерной. Она может быть относительной, определяемой как отношение одноимённых величин (например, относительная диэлектрическая проницаемость), или логарифмической, определяемой как логарифм относительной величины (например, логарифм отношения мощностей или напряжений).
При определении размерности производных ФВ руководствуются следующими правилами:
1. Размерности левой и правой частей уравнения равны между собой.
2. Алгебра размерностей мультипликативна, т.е. состоит из умножения.
3. Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между величинами имеет вид
Q = A⋅ B ⋅C , то
dimQ = dim A⋅dimB⋅dimC .
4. Размерность частного при делении одной величины на другую равна отношению их размерностей.
5. Размерность любой величины, возведенной в степень, равна её размерности в той же степени. Так, если Q = An, то
dim Q = ∏1n dim A = dimn A
Размерность является качественной характеристикой измеряемой величины. Она отражает её связь с основными ФВ и зависит от выбора последних.
Например, если скорость определяется по формуле V=l/t, то dim V = dim l / dim t = L/T = LT-1.
Таким образом, всегда можно выразить размерность производной ФВ через размерность основных ФВ с помощью выражения dim Q = LαMβTγ….
Понятие размерности используется:
– для перевода единиц из одной системы в другую
– для проверки правильности сложных расчетных формул
– при выяснении зависимости между величинами
Количественная характеристика измеряемых величин
Для того чтобы можно было установить для каждого объекта различия в количественном содержании свойства, отображаемого физической величиной, в метрологии введены понятия ее размера и значения.
Размер физической величины – это ее количественная определенность, присущая конкретному материальному объекту, системе, явлению или процессу.
Например, каждое тело обладает определенной массой, вследствие чего тела можно различать по их массе, т.е. по размеру интересующей нас ФВ.
Размер является объективной количественной характеристикой, не зависящей от выбора единиц измерений. Например, 1000 мг; 1 г; 0,001 кг – три варианта представления одного и того же размера. Каждый из них является значением физической величины (в данном случае – массы) – выражением размера в тех или иных единицах измерений.
Значение физической величины – это выражение размера физической величины в виде некоторого числа принятых для нее единиц.
Значение физической величины Q можно представить в виде произведения:
Q = q [Q], (основное уравнение измерения)
где q – отвлечённое число, называемое числовым значением,
[Q] – размер единицы измерения данной ФВ.
Значение ФВ находится путем измерения или вычисления в соответствии с основным уравнением измерения. Из приведённых примеров видно, что для одного и того же размера числовое значение тем меньше, чем больше единица измерения (и наоборот), так что произведение в правой части основного уравнения измерения остается постоянным.
Единица физической величины – это ФВ фиксированного размера, которой условно присвоено числовое значение, равное единице. Она применяется для количественного выражения однородных ФВ.
Размер единицы физической величины – количественная определенность единицы физической величины, воспроизводимой или хранимой средством измерений.
Не следует для выражения количественных соотношений применять словосочетания типа «величина массы», «величина длины», т.к. масса и длина сами являются величинами. Не принято говорить «размер массы (длины, силы,)», «значение массы (длины, силы, )», говорят просто «масса (длина, сила,)».
Из-за зависимости числовых значений от размеров единиц ФВ, роль последних очень велика. Если допустить произвол в выборе единиц, то результаты измерений будут несопоставимы между собой, т.е. нарушится единство измерений. Чтобы этого не произошло, единицы измерений устанавливаются по определённым правилам и закрепляются законодательным путём. Наличие законодательной метрологии отличает метрологию от других естественных наук (физики, химии и др.) и направлено на обеспечение единства измерений.