Ремизов а.Н., Максина а.Г., Потапенко а.Я. Медицинская и биологическая физика: учеб. Для вузов. – 9-е изд., м.: Дрофа, 2009. (см. Раздел по теории вероятностей и математической статистике).
Дополнительная:
Вентцель Е. С. Теория вероятностей: учебник для вузов / Вентцель Е. С. . - 7-е изд., стер. - М. : Высш. шк. , 2001 . - 575 с.
Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие / Гмурман В. Е. . - 8-е изд., стер. - М.: Высш. шк. , 2002. - 480 с. : ил.
Мятлев В. Д. Теория вероятностей и математическая статистика. Математические модели: учеб. пособие / Мятлев В. Д., Панченко Л. А., Ризниченко Г. Ю. и др. - М.: Академия , 2009 . - 316 с. : ил. . - Университетский учебник. Высшая математика и её приложения к биологии . - Библиогр.: с. 307-311.
К ЗАНЯТИЮ «УТВЕРЖДАЮ»
04.03.13-09.03.13 Зав. кафедрой С.А. Коробкова
Методические указания № 5 к занятию по математике для студентов лечебного факультета специальности – 060101 «Лечебное дело». Элементы математической статистики. Текущий контроль по математике
I часть
ОСНОВНЫЕ ВОПРОСЫ:
Предмет и задачи математической статистики.
Понятие генеральной и выборочной совокупности. Свойства выборки: репрезентативность и объем. Понятие малой и большой выборки.
Способы группировки исходных статистических данных: ранжирование, составление вариационного ряда, построение графиков вариационных рядов (полигонов и гистограмм).
Точечные оценки выборочной совокупности: выборочная средняя, дисперсия и исправленная дисперсия, мода, медиана.
Интервальные оценки генеральной совокупности по ее выборке: доверительная вероятность и доверительный интервал.
РЕШИТЬ ЗАДАЧУ: см. задание 3 задача 5) ВАРИАНТА 0.
II ЧАСТЬ
ЗАДАНИЕ: Самостоятельно подготовиться к выполнению контрольного задания по математике на занятии:
Повторить изученные вопросы по высшей математике и теории вероятностей.
Повторить правила решения типовых заданий по математике, ориентируясь на контрольное задание:
Вариант 0
1. Вычислить производные следующих функций:
1)
,
2)
,
3)
,
4)
.
2. Вычислить интегралы:
1)
2)
.
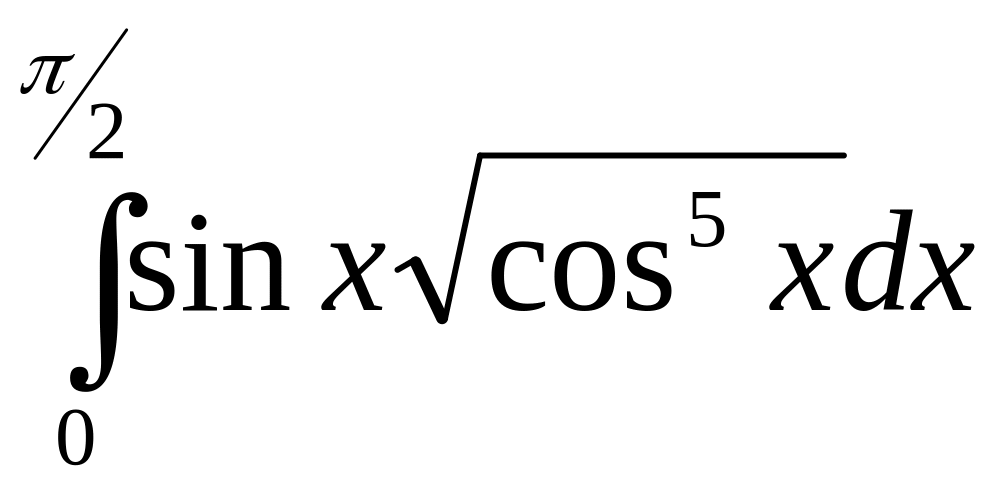3. Решить задачи:
Рабочий обслуживает два станка. Вероятность того, что в течение часа первый станок потребует внимания рабочего, равна 0,3, второй - 0,4. Найти вероятность того, что в течение часа а) ни один станок не потребует внимания рабочего; б) хотя бы один станок потребует внимания рабочего.
Принимая вероятность появления мальчика при рождении ребенка равной 0.5, найти вероятность того, что в семье с 7 детьми по крайне мере 5 девочек.
Случайная величина задана следующим законом распределения:
-
X
-10
-5
0
5
10
P
0.2
0.3
0.1
0.1
?
Найти неизвестную вероятность, математическое ожидание и среднеквадратическое отклонение, составить функцию распределения случайной величины.
В нормальном законе распределения математическое ожидание равно 35, дисперсия равна 6. Найти вероятность того, что случайная величина принимает значения больше 30.
У 15 матерей, имеющих порок сердца, родились дети с массой тела: 3.0 2.6 2.7 3.0 3.1 2.8 2.8 2.3 2.9 2.8 2.6 2.3 2.9 2.8 2.7. Вычислить числовые характеристики выборочной совокупности, найти доверительный интервал для генеральной средней
.
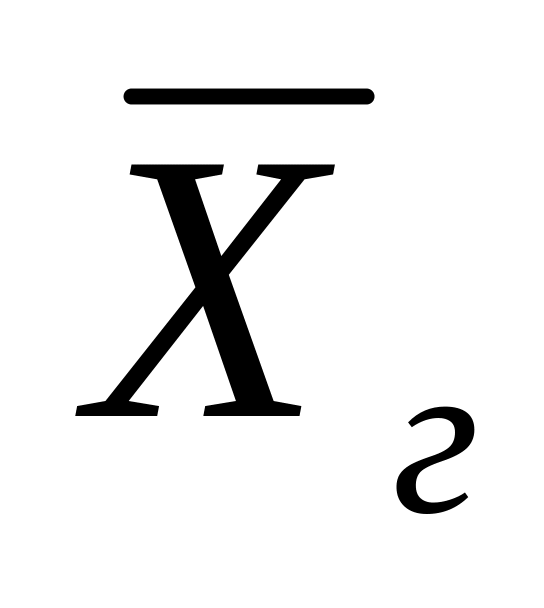Принять уровень значимости
к занятиям по физике
11.03.13-16.03.13 «Утверждаю»
18.03.13-23.03.13 Зав. каф. физики ВолгГМУ С.А. Коробкова