Міністерство освіти і науки, молоді та спорту україни

ІВАНО-ФРАНКІВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ НАФТИ І ГАЗУ

Кафедра комп’ютерних технологій в системах управління та автоматики

Дисципліна “Системи передавання даних”

ЛАБОРАТОРНА РОБОТА №4

Моделювання алгоритмів амплітудної, фазової і частотної маніпуляції сигналів в matlab 6.X

Івано-Франківськ

1. Тема: Моделювання алгоритмів амплітудної, фазової і частотної маніпуляції сигналів в matlab 6.X

2 Мета роботи:

• вивчення принципів цифрової модуляції і маніпуляції;

• програмна імітація цифрової модуляції і маніпуляції;

• розширення і поглиблення знань з відповідного розділу предмету.

3. Устаткування:

2.1 ПК ІВМ РС на базі x86 CPU.

2.2 ПЗ MathWorks MATLAB® 5.3.1/6.0/6.1/6.5/7.0

4.1 Теоретичні відомості:

В даний час все більше інформації, що передається по різноманітним каналам зв’язку, існує в цифровому вигляді. Це означає, що передачі підлягає не неперервний (аналоговий) модулюючий сигнал, а послідовність цілих чисел n₀, n₁, n₂, …, які можуть приймати значення із деякої фіксованої множини. Це числа, що називаються символами (symbol), надходять від джерела інформації з періодом T, а частота що відповідає відповідному періоду, називається символьною швидкістю (symbol rate): f_T = 1/T.

Зауваження. Часто використовуваною на практиці є двійкова (binary) послідовність символів, коли кожне із чисел n_і може приймати одне із двох значень – 0 або 1. Послідовність символів, що передаються є, очевидно, дискретним сигналом. Оскільки символи приймають значення із кінцевої множини, цей сигнал фактично є і квантова ним, тобто його можна назвати цифровим сигналом. Далі будуть розглядатися питання, пов’язані з перетворенням цього цифрового сигналу в аналоговий модульований сигнал.

Типовий підхід при здійсненні передачі дискретної послідовності символів полягає в наступному. Кожному із можливих значень символу співставляється деякий набір параметрів несучого коливання. Ці параметри підтримуються постійними на протязі інтервалу T, тобто до надходження наступного символу. Фактично це означає перетворення послідовності чисел {n_k} в ступінчатий сигнал s_n(t) з використанням кусочно-постійної інтерполяції:

s_n(t) = f(n_k), kT   t < (k + 1)T.

Тут f — деяка функція перетворення. Отриманий сигнал s_n(t) далі використовується в якості модулюючого сигнау звичайним способом.

Такий спосіб модуляції, коли параметр несучого коливання міняється скачкоподібно, називається маніпуляцією (keying). В залежності від того, які саме параметри міняються, розрізняють амплітудну (АМн), фазову (ФМн), частотну (ЧМн) маніпуляцію.

Амплітудна маніпуляція

Як буде показано далі, амплітудна маніпуляція (АМн; англійськй термін — amplitude shift keying, ASK), маніпуляція при якій скачкоподібно міняється амплітуда несучого коливання. Тут ми побудуємо в якості прикладу графік АМн-сигналу.

Приклад

Амплітудна маніпуляція здійснюється функціями dmod (формується дійсний вихідний сигнал) і dmodce (формується комплексна огинаюча) пакету Communications при вказанні в низ параметра типу модуляції 'ask'. Настуний за ним пераметр М вказує кількість використовуваних рівнів маніпуляції. Символи, що підлягають передачі повинні приймати цілочисельне значення, що лежать в діапазоні 0…M–1. Символу 0 відповідає значення амплітуди, рівне -1, а символу М-1 – значення амплітуди, рівне 1. Решта рівні рівномірно роз приділені між цими значеннями. Таким чином строго говорячи, в даному випаду може мінятися не тільки амплітуда, а ле й фаза несучого коливання (відємні амплітудні множники відповідають зміні фази на 180⁰).

В якості прикладу побудуємо графік сигналу, що буде містити всі можливі символи при 8-позиційній АМн:

M = 8; % кількість рівнів маніпуляції

sy = 0:M-1; % передаваємі символи

Fd = 1; % символьна швидкість

Fc = 4; % несуча частота

FsFd = 40; % відношення Fs/Fd

Fs = Fd * FsFd; % частота дискретизації

% формуємо АМн-сигнал

[s_ask, t] = dmod(sy, Fc, Fd, Fs, 'ask', M);

plot(t, s_ask)

grid on

На графіку добре видно викид фази в середині сигналу. Крім того, можна помітити що фази посилок в першій і другій половинах сигналу, що мають одинакову амплітуду, відрізняються на 180⁰.

Фазова маніпуляція

Фазова маніпуляція (ФМн); англійський термін - phase shift keying, PSK, при якій скачкоподібно змінюється фаза несучого коливання.

На прктиці фазхова маніпуляція використовується в невеликій кількості можливих значень початкової фази – як правило, 2, 4 або 8. Крім того, при прийомі сигналу складно виміряти абсолютне значення початкової фази; значно простіше визначити відносний фазовий зсув між двома сусідніми символами. Тому переважно використовується фазорізнецева маніпуляція.

Демодуляція фазової маніпуляції може виконуватись тим же методом, що і у випадку квадратурної маніпуляції (шляхом множення на несуче коливання). Застосовуючи до ФМн, даний метод демодуляції часто називають кореляційним.

Приклад

Фазова маніпуляція здійснюється функціями dmod (формується дійсний вихідний сигнал) і dmodce (форується комплексна огинаюча) пакету Communications при вказанні в них параметра типу модуляції 'psk'. Наступний за ним параметр M вказує на кількість значень градацій початкової фази. Символи що підлягають передачі, повинні приймати цілочисельне значення, що лежить в діапазоні 0…M–1. Символу k відповідає значення початкової фази, рівне 2 k/M радіан, або 360k/M градусів.

В якості прикладу побудумо графі сигналу, що містить всі можливі символи при 4-позиційній ФМн:

M = 4; % кількість позицій маніпуляції

sy = 0:M-1; % передаваємі символи

Fd = 1; % символьна швидкість

Fc = 4; % несуча частота

FsFd = 40; % відношення Fs/Fd

Fs = Fd * FsFd; % частота дискретизації

% формуємо ФМн-сигнал

[s_psk, t] = dmod(sy, Fc, Fd, Fs, 'psk', M);

plot(t, s_psk)

На графіку помітні скачки фази при переході від одного символу до другого.

Частотна маніпуляція

При частотній маніпуляції, кожному можливому значенню предаваємого символу співставляється своя частота. На протязі кожного символьного інтервалу передаються гармонічні коливання з частотою. Що відповідає текучому символу. При цьому можливі різні варіанти, що відрізняються вибором початкової фази окремих синусоїдальних посилок. Перший спосіб – коли всі посилки, що відповідають одному закону передаваємого символу, мають однакову початкову фазу, тобто є ідентичними. При цьому можна попередньо сформувати набори відліків для всіх можливих дискретних символів. Тоді здійснення частотної маніпуляції зводиться до послідовної передачі попередньо розрахованих послідовностей відліків, що відповідають поступаючим символам. Однак якщо використовувані частоти маніпуляції не кратні символьній швидкості, сформований таким чином ЧМн-сигнал буде містити розриви (скачки) на стиках символів. Внаслідок цього спектр сигналу буде мати всплески на частотах, кратних символьній швидкості. Другий спосіб – неперервна генерація коливань всіх необхідних частот і здійснення переключення між цими сигналами у відповідності з поступачими символами. Даний метод також не гарантує відсутність сачків на стиках символів, але внаслідок того, що початкові фази символів міняються від символу до символу, скачки виникають не на стиках а їх величина виявляється різною. В результаті виникаючі через скачки всплески спектри в даному випадку виражені слабо. Через це варіант формування ЧМн-сигналу використовується у функціях dmod і dmodce пакету Communications.

На кінець третій спосіб – коли поступаючи для передачі символи керують швидкістю лінійного наростання текучої фази, а частотно-маніпульований сигнал формується шляхом обчислення косинуса цієї фази. При цьому фазова функція, а отже і сам ЧМн-сигнал є неперервним (не має сачків). Даний спосіб складніший в реалізації, але він дає найбільш компактний спектр сигналу. ЧМн-сигнал, отриманий таким чином, називається частотно-маніпульованим сигналом з неперервною фазовою функцією.

Приклад

Частотна маніпуляція здійснюється функціями dmod (формується дійсний вихідний сигнал) і dmodce (формується комплексна огинаюча) пакета Communications при указании в них параметра типа модуляції 'fsk'. Наступні за ним параметри M і tone вказують відповідно кількість використовуваних частот маніпуляції і відстань між сусідніми частотами (по ізамовчуванню значення параметра tone рівне символьній швидкості Fd). Символи, що підлягають передачі, повинні приймати цілочисельне значення, що лежить в діапазоні 0…M–1. Символу k відповідає зміщення частоти (відносно несучої частоти Fc), рівне tone*(1–M+2*k)/2.

В якості прикладу сформуємо 2-позиійний (бінарний) ЧМн-сигнал, в якому можливим значенням символів 0 і 1 відповідають частоти 800 и 1600 Гц. Символьна швидкість буде рівна 400 символам в секунду, а частота дискретизації — 16 кГц:

bits = [0 1 0 0 1]; % цифрове повідомлення

N = length(bits); % довжина повідомлення

Fd = 400; % символьна швидкість

FsFd = 40; % відношення Fs/Fd

Fs = Fd * FsFd; % частота дискретизації

f0 = 800; % частота маніпуляції для символу "0"

f1 = 1600; % частота маніпуляції для символу "1"

Fc = (f0 + f1)/2; % несуча частота

tone = f1 – f0; % рознос частот

% формуємо ЧМн-сигнал

[s_fsk, t] = dmod(bits, Fc, Fd, Fs, 'fsk', 2, tone);

td = t * Fd; % час для графіку – в символах

plot(td, s_fsk)

xlabel('Symbols')

ylabel('s_{FSK}')

ylim([-1.1 1.1])

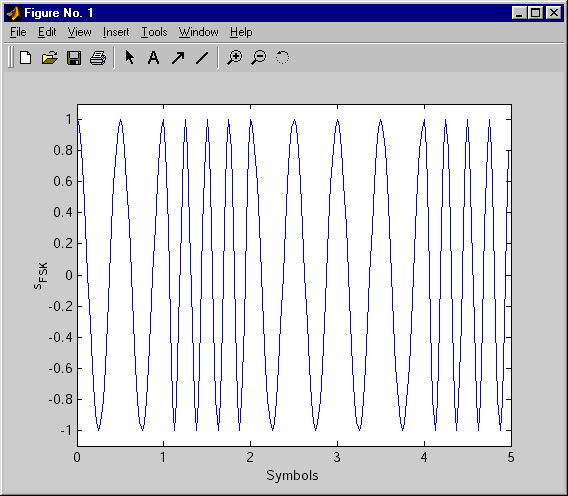
На графіку добре помітні двократні зміни частоти сигналу при зміні значення передаваємого біту. В даному прикладі на довжині символу укладається два періоди коливань при передачі нульового біту і чотири періоди — при передачі одиничного біту.