3.2. Индуктивности прямолинейных проводников прямоугольного поперечного сечения

В лабораторной работе исследуются индуктивные связи в системах па­раллельных проводников с прямоугольным поперечным сечением. Выраже­ния для индуктивностей в таких системах могут быть получены с примене­нием соотношений, приведенных выше при рассмотрении вспомогательной задачи, в ряде случаев в сочетании с методом наложения. Ниже приведены формулы для расчета индуктивностей для частных случаев системы провод­ников.

1. Собственная индуктивность плоского контура, образованного полосковыми проводниками на печатной плате (рис. 2.8)

Выражение для удельной (погонной), т. е. отнесенной к единице длины проводника, индуктивности такой системы [2, стр. 144] имеет вид:

, (2.10)

Полная индуктивность контура .

Рис. 2.8. Плоский контур, образованный параллельными полосковыми проводниками и перемычкой между ними

Выражение (2.10) получено в приближении нулевой толщины t полосковых проводников.

2. Взаимная индуктивность параллельных двухпроводных линий пере­дачи, образованных параллельными одинаковыми проводниками (рис. 2.9)

Рис. 2.9. Поперечное сечение двух индуктив­но связанных линий (I и II), образо­ванных из параллельно расположен­ных проводников с одинаковым поперечным сечением

В общем случае выражение для погонной (удельной) взаимной индук­тивности двух двухпроводных линий имеет вид [2, стр. 177]:

, (2.11)

где - произведение средних геометрических расстояний площадей поперечных сечений отдельных проводов первой линии от площадей попе­речных сечений отдельных проводов второй линии, причем в это произве­дение входят все расстояния для проводов с токами противоположного на­правления;

- произведение средних геометрических расстояний площадей поперечных сечений отдельных проводов первой линии от площадей попе­речных сечений отдельных проводов второй линии, причем в это произве­дение входят все расстояния для проводов с токами одинакового направле­ния.

Если все провода, как в нашем случае, прямолинейные, то отдельные средние геометрические расстояния , входящие в эти произведения, можно заменить расстояниями между центрами инерции (или осями) поперечных сечений соответствующих проводов.

Отметим, что после замены в формуле (2.11) средних геометрических расстояний на расстояния ; между центрами инерции поперечных сече­ний соответствующих проводов эта формула оказывается справедливой для линейных проводов при однородной плотности распределения тока по поперечному сечению проводников.

Полная взаимная индуктивность М двух таких контуров, образованных полосковыми проводниками одинаковой длины, рассчитывается по формуле , где l - длина линий передачи.

С учетом сказанного легко получить выражения для частных случаев связанных двухпроводных линий.

2.1. Взаимная индуктивность М двух контуров, образованных одина­ковыми полосковыми проводниками, лежащими в одной плоскости

Четыре полосковые проводника, лежащие в плоскости, позволяют сфор­мировать три типа связанных контуров, представленных на рис. 2.10.

а б

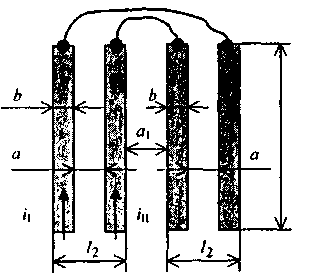
в

Рис. 2.10. Два плоских контура, образованные двумя парами одинаковых парал­лельных полосковых проводников и перемычками между проводниками каждой пары: а, б, в - варианты

2.1.1. Первый вариант образования контуров (см. рис. 2.10, а).

Взаимная индуктивность такой системы контуров

. (2.12)

Заметим, что выражение (2.12) определяет модуль взаимной индуктивности.

В частном случае равенства расстояний , что соответствует мо­дели, применяемой в данной лабораторной работе, выражение (2.12) запи­шется в виде:

2.1.2. Второй вариант образования контуров (см. рис. 2.10, б).

Взаимная индуктивность такой системы контуров

. (2.13)

Выражение (2.13) определяет модуль взаимной индуктивности.

В частном случае равенства расстояний , что соответствует мо­дели, применяемой в данной лабораторной работе, выражение (2.13) запи­шется в виде:

.

2.1.3. Третий вариант образования контуров (см. рис. 2.10, в).

Взаимная индуктивность такой системы контуров

. (2.14)

Выражение (2.14) определяет модуль взаимной индуктивности.

В частном случае равенства расстояний , что соответствует мо­дели, применяемой в данной лабораторной работе, выражение (2.14) запи­шется в виде:

.

2.2. Взаимная индуктивность М двух контуров, расположенных в параллельных плоскостях и образованных одинаковыми полосковыми проводниками, попарно лежащими в одной плоскости (рис. 2.11)

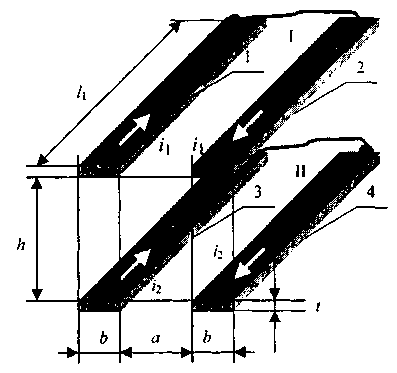
Рис. 2.11. Два плоских контура (I и II), образованные двумя парами одинаковых па­раллельных полосковых проводников и перемыч­ками между проводника­ми каждой пары и разме­щенные в параллельных плоскостях

Взаимная индуктивность системы контуров

. (2.15)

Выражение (2.15) определяет модуль взаимной индуктивности.

Анализ выражения (2.15) показывает, что при уменьшении , на­пример при стремлении этой суммы к нулю, подлогарифменное выражение стремится к бесконечности и, следовательно, стремится к бесконечности (резко возрастает) величина взаимной индуктивности М. Это соответствует положению теории (ожидаемой индуктивности), так как такой предельный переход обращает рассматриваемую систему в бесконечно тонкий (замкну­тый) проводник.