1. Система двух протяженных плоских параллельных проводников, размещенных в одной плоскости

Такая система проводников образует структуру полосковых линий свя­зи, которая в технике называется копланарной системой.

Погонная емкость между проводниками в такой системе: - в однородной среде с диэлектрической проницаемостью (рис.1.4):

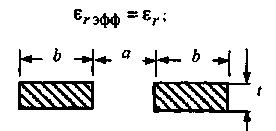
Рис.1.4. Поперечное сечение двух полосковых проводников в однородной среде

(1.2)

(1.3)

- на диэлектрическом основании (теоретически бесконечном диэлектрическом слое) с > 1 (рис. 1.5).

Рис.1.5. Поперечное сечение двух полосковых проводников на диэлектрическом основании

Эффективная диэлектрическая проницаемость определяется по приближенной формуле

,

а коэффициент формы sf определяется выражениями (1.2) и (1.3).

2. Система двух плоских параллельных полосковых проводников, расположенных параллельно один над другим

Рассмотрим погонную емкость этой системы проводников в разных сре­дах:

- в однородной среде с диэлектрической проницаемостью (рис. 1.6):

(1.4)

Рис.1.6. Поперечное сечение двух шин (системы параллельных плоских проводников), размещённых в однородной среде

ф- на бесконечной диэлектрической пластине с ег> 1, т.е. если плоские проводники разделены слоем диэлектрика (рис. 1.7):

(1.5)

а коэффициент формы также, как и предыдущем случае, определяется по формуле (1.4).

Рис.1.7. Поперечное сечение двух шин, разделённых слоем диэлектрика

3. Одиночный полосковый проводник над проводящей плоскостью

Такая конструкция (рис. 1.8) называется несимметричной полосковой линией или в технике сверхвысоких частот - микрополосковой линией. По­перечный размер L диэлектрической пластины и размер проводящей поверх­ности экрана теоретически бесконечны, а практически должны быть в 3-5 раз большими, чем поперечный размер b проводника, так как при этом электро­магнитное поле в поперечном сечении линии при удалении от продольной оси в поперечном направлении уже практически затухает более, чем на поря­док.

Рис. 1.8 Поперечное сечение несимметричной полосковой линии

Коэффициент формы несимметричной полосковой линии при b > h и b >> t имеет вид

(1.6)

а эффективная диэлектрическая проницаемость приближенно определяется формулой (1.5).

4 . Протяженная пластина, симметрично расположенная между параллельными проводящими плоскостями

Такая конструкция называется симметричной полосковой линией (рис. 1.9). Для симметричной полосковой линии при однородном за­полнении диэлектриком пространства между параллельными проводящими (экранирующими) плоскостями формула для расчета коэффициента формы при b> 1,117h и b>>t имеет вид

(1.7)

Эффективная диэлектрическая проницаемость равна диэлектрической проницаемости диэлектрика.

Рис.1.9. Поперечное сечение симметричной полосковой линии

Приведенные выражения исчерпывают известные приближенные соотношения для оценочного расчета конденсаторных емкостей простейших линий связи. Очевидно, что получаемые с применением этих формул вели­чины емкостей соответствуют нижней границе возможных реальных значе­ний (при выделении пары проводников в системе рис. 1.2), так как не учиты­вают параллельных емкостных связей между ними за счет соседних провод­ников. Это следует из аналогии задачи о рабочей емкости двухпроводной ли­нии над проводящей поверхностью [3]. Для более сложных вариантов линий, образованных протяженными (бесконечно длинными) параллельными по­лосками, размещенными в плоскости, необходимо использовать формулы для расчета частичных емкостей, приведенные в [2], которые дают точные выражения, полученные методом конформных преобразований.