2. Методические указания по выполнению контрольной работы
2.1. Статистический анализ в ms Excel. Надстройка Пакет анализа
2.1.1. Общие сведения о надстройке Пакет анализа
Пакет анализа – это надстройка MS Excel, обеспечивающая доступ к набору средств анализа, которые предназначены для решения сложных статистических и инженерных задач.
Для проведения анализа данных с помощью этих инструментов следует указать входные данные выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон.
Чтобы вывести список доступных инструментов анализа, необходимо выбрать в меню Сервис команду Анализ данных. Если указанная команда отсутствует, следует загрузить Пакет анализа, выполнив команду СервисНадстройкиПакет анализа.
После окончания загрузки в списке опций пункта Сервис появится строка Анализ данных. При выборе этой строки появляется диалоговое окно Анализ данных, в котором отображается список инструментов анализа данных.
2.1.2. Скользящее среднее
Инструмент Скользящее среднее является инструментов для прогнозирования и используется для сглаживания и прогнозирования очень изменчивого набора данных. Во многих случая скользящее среднее позволяет обнаружить тенденции, которые по-другому сложно заметить из-за большого разброса данных.
Сглаживание и прогнозирование ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень (значение) из определенного числа первых по порядку уровней (значений) ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее – начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
Например, если для сглаживания ряда вы выбрали скользящее среднее за три месяца (февраль, март, апрель), то средним значением за апрель будет среднее значение показателей за эти три месяца.
Для сглаживания ряда значение скользящей средней определяют по формуле:
, (6)
где Ft – прогнозируемое значение ряда;
m – число уровней интервала сглаживания, по умолчанию m =3;
Аt-i+1 – значение текущего уровня ряда динамики;
t – порядковый номер уровня ряда динамики;
i – порядковый номер уровня в интервале сглаживания, i=1, 2, …, m.
Интервал сглаживания, т.е. число входящий в него уровней m, определяют, используя следующее правило: если необходимо сгладить мелкие, беспорядочные колебания, то интервал сглаживания берут по возможности большим; если же нужно сохранить более мелкие волны и освободиться от периодически повторяющихся колебаний, интервал сглаживания уменьшают.
В качестве m выбирается нечетное число, обычно 3, 5 или 7, и эти схемы называют трехточечной, пятиточечной и т.д.
Например, если необходимо сгладить ряд динамики по трехточечной схеме (m=3), то первое значение сглаженного ряда будет вычисляться как средний уровень первых трех значений динамики ряда. Ряд будет начинаться со значения 3-го уровня:
t=3,
. (7)
Следующие значения сглаженного ряда вычисляются аналогично:
t=4,
, (8)
t=5,
и т.д. (9)
Для составления прогноза методом скользящего среднего значения ряда прогноза вычисляют как среднее трех предыдущих показателей ряда динамики. Например, если вы выбрали скользящее среднее за три месяца (февраль, март, апрель), то среднее значение показателей за эти три месяца будет прогнозом на май.
Для составления прогноза методом скользящего среднего используют формулу:
.
(10)
Если необходимо сгладить ряд динамики по трехточечной схеме (m=3), то первое прогнозируемое значение ряда будет вычисляться как средний уровень первых трех значений динамики ряда. Ряд прогноза будет начинаться со значения 4-го уровня:
t=3,
. (11)
Следующие значения прогноза вычисляются аналогично:
t=4,
, (12)
t=5,
и т.д. (13)
В пакете Анализ данных инструмент Скользящее среднее используется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов.
При необходимости в качестве параметров вывода Excel предлагает вывод Стандартных погрешностей. Значения стандартных погрешностей показывают степень различия между настоящими значениями и вычисленными средними.
Если предшествующих данных недостаточно для построения прогноза, Excel возвратит ошибочное значение #Н/Д.
Выходной диапазон и исходные данные должны находиться на одном листе. По этой причине параметры Новый лист и Новая книга недоступны.
Сглаживания ряда урожайности.
Имеются данные о средней урожайности зерновых культур в хозяйстве за 1990-2005 года (таблица 19).
Таблица 19
Год |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
Ср.урожайность, ц/га |
9,3 |
13,5 |
12,4 |
14,2 |
13,5 |
15,4 |
15,1 |
14,3 |
17,8 |
15,6 |
11,2 |
18,0 |
15,6 |
18,9 |
14,5 |
15,3 |
|
Сгладить временной ряд методом скользящей средней (трехточечная схема). Составить прогноз средней урожайности на 2006 г.
Пояснения к задаче.
Представленный временной ряд имеет изменчивые значения, поэтому для его сглаживания и прогнозирования целесообразно использовать метод скользящего среднего. Для данной задачи число уровней, входящих в интервал сглаживания m=3 (метод трехлетней средней).
Первой величиной сглаженного ряда будет значение за 1992 г., рассчитанное как среднее значение ряда динамики с 1990 г. по 1992 г.
Первой величиной ряда прогноза будет значение для 1993 г., рассчитанное как среднее значение ряда динамики с 1990 г. по 1992 г.. Прогноз на 2006 г. будет рассчитываться как среднее значение ряда динамики с 2003 г. по 2005 г.
В ходе решения задачи сначала вычислим значения скользящего среднего по соответствующим формулам, далее определим значения сглаженного ряда и ряда прогноза с помощью инструмента Скользящее среднее.
Ход решения задачи.
Создайте таблицу согласно рисунку 33.
В ячейке D6 по формуле (7) рассчитайте первое значение сглаженного ряда (рис. 34).
Рис. 33. Исходная таблица Сглаживание ряда урожайности
Рис. 34. Расчет значений ряда Скользящее среднее
Используя Автозаполнение скопируйте данную формулу в диапазон ячеек Е6:Q6 (см. рис. 34). Таким образом будут получены остальные значения сглаженного ряда.
Выполните команду СервисАнализ данных. В диалоговом окне Анализ данных выберите инструмент анализа Скользящее среднее.
В диалоговом окне Скользящее среднее укажите Входной интервал – диапазон ряда динамики (В5:Q5). Введите Интервал – число уровней интервала сглаживания m=3. Укажите первую верхнюю ячейку Выходного интервала – ячейку, соответствующую первому значению сглаженного ряда (B7). Выберите параметры Вывод графика и Стандартные погрешности. В результате диалоговое окно Скользящее среднее должно иметь вид, представленный на рисунке 35.
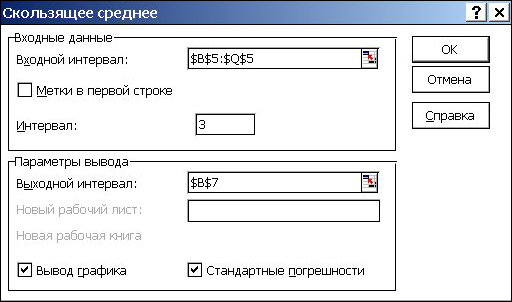
Рис. 35. Диалоговое окно Скользящее среднее
Нажмите кнопку ОК. Программа выведет значения сглаженного ряда и стандартных погрешностей (рис. 36).
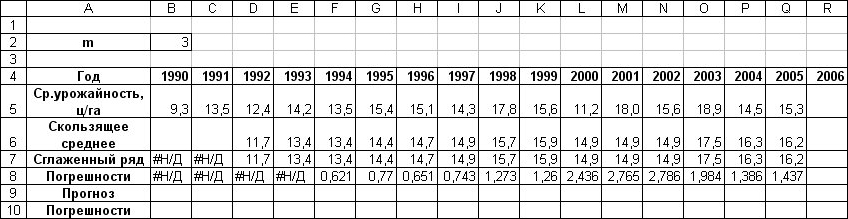
Рис. 36. Рассчитанные значения сглаженного ряда и стандартных погрешностей
Убедитесь, что значения скользящего среднего, рассчитанные по формулам и полученные с помощью Пакета анализа, идентичны.
Выполните команду СервисАнализ данных. В диалоговом окне Анализ данных выберите инструмент анализа Скользящее среднее.
Заполните диалоговое окно Скользящее среднее согласно рисунку 37. Обратите внимание, что в качестве Выходного интервала указывается вторая ячейка ряда прогноза.
Рис. 37. Диалоговое окно Скользящее среднее
Заметьте, что в таблице результатов каждый показатель скользящего среднего сдвинут на одну позицию по сравнению с рядом прогноза (рис. 38). Это значит, что прогнозом для четвертого периода является первое вычисленное скользящее среднее.
Добавьте ряд прогноза в диаграмму, отформатируйте диаграмму согласно рисунку 39.
Сохраните файл.
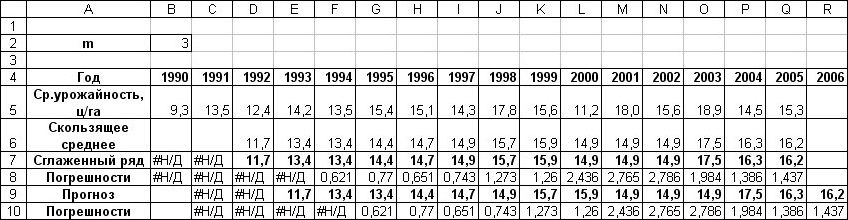
Рис. 38. Рассчитанные значения ряда Прогноз
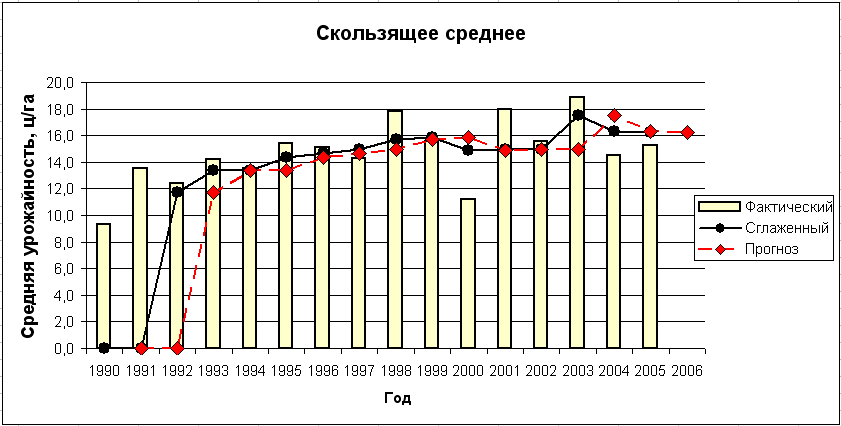
Рис. 39. Диаграмма Скользящее среднее