5. Поле волны н10 в прямоугольном волноводе

Основным, или низшим, типом волны называется такой тип волны, который обладает наибольшей критической длиной волны при данных размерах волновода. Поперечные размеры волновода для заданной частоты берутся наименьшие.

В прямоугольном волноводе низшим типом волны является волна Н₁₀, учитывая, что a > b. Для такой волны критическая длина имеет значение

(4.12)

Передачу энергии по прямоугольному волноводу производят часто с помощью волны Н₁₀. Структура поля волны Н₁₀ описывается формулами.

(4.13)

Поперечное волновое число g определяется формулой

(4.14)

Формулы (4.13), описывающие структуру поля волны Н₁₀ можно записать несколько иначе

(4.15)

Структура поля волны Н₁₀ приведена на рис. 4.8.

Рис. 4.8

Ф азовая скорость распространения волны Н₁₀ в волноводе определяется как

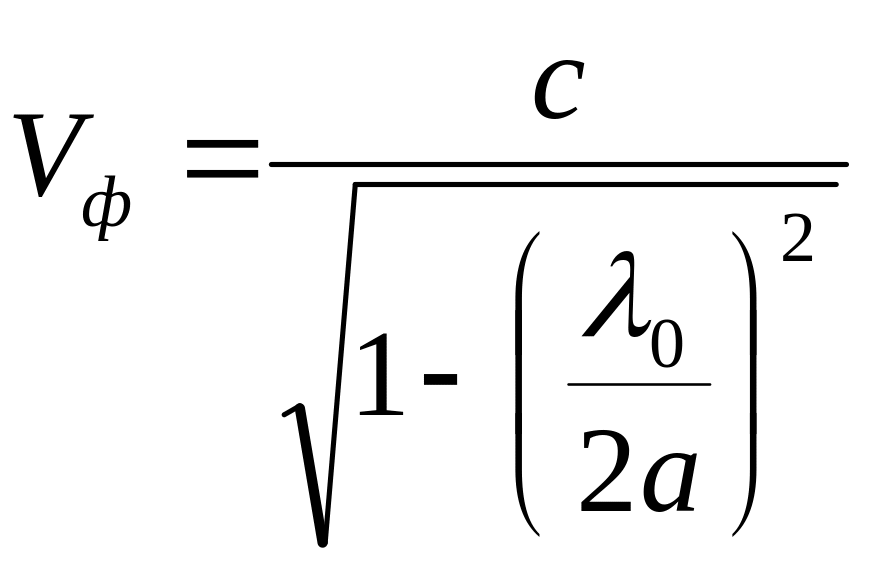(4.16)

Д лина волны в волноводе отличается от длины волны в свободном пространстве и определяется

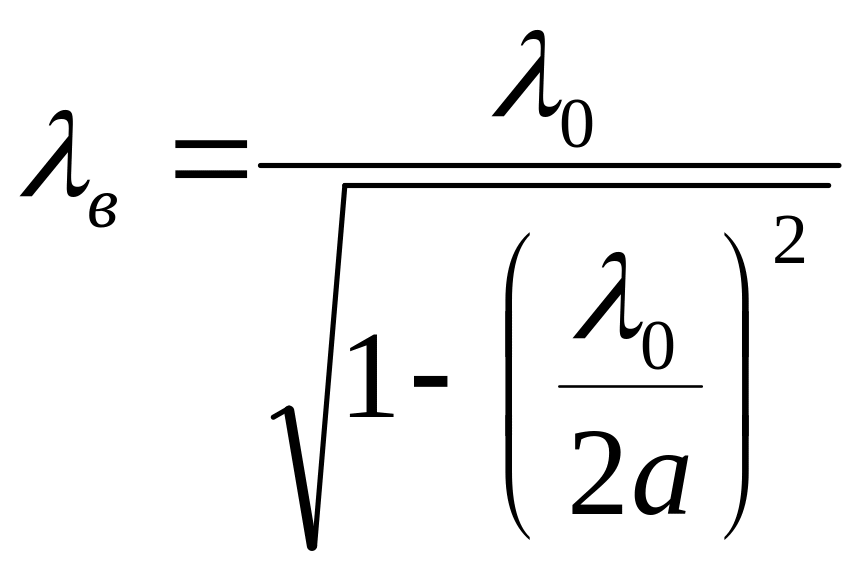(4.17)

В олновое сопротивление волновода находится из формулы

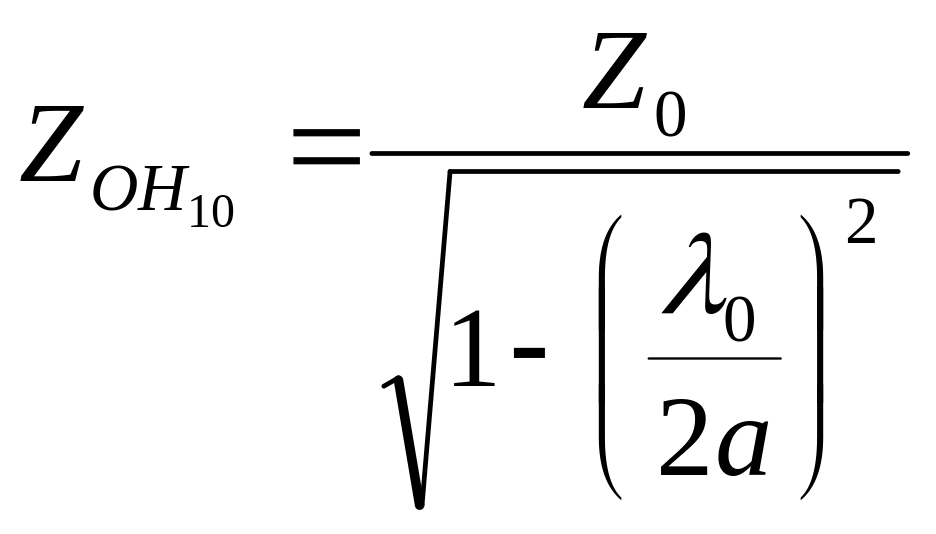(4.18)

где Z₀ – волновое сопротивление среды, заполняющей волновод, .

Заметим интересный факт. Магнитное поле, как следует из формул (4.13), (4.15) , имеет две составляющие, амплитуды которых зависят от координат рассматриваемой точки. Эти составляющие сдвинуты в пространстве и времени на 90^. Отсюда видно, что магнитное поле волны Н₁₀ имеет эллиптическую поляризацию.

Внутри волновода выполняются условия для протекания поверхностного тока . Картина поверхностных токов приведена на рисунке 4.9.

Рис. 4.9

Определим мощность, которая переносится основной волной Н₁₀. значение модуля вектора Пойнтинга определяется

(4.19)

Тогда мощность, переносимая через поперечное сечение проводника с учетом усреднения во времени, определяется формулой

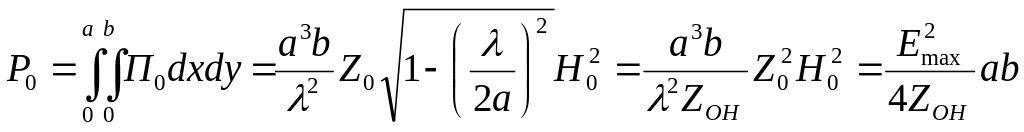
, (4.20)

где - максимальная амплитуда электрического поля при ,

- волновое сопротивление прямоугольного волновода при распространении волны Н₁₀.

При заданных размерах волновода диапазон рабочих длин волн определяется соотношением

(4.21)

В прямоугольном волноводе также существуют и волны Е-типа, в которых также имеются и продольная и поперечная составляющие поля. Так как волна распространяется вдоль оси z, то уравнение Гельмгольца для составляющей E_Z имеет вид

(4.22)

Решением уравнения Гельмгольца с учетом выполнения граничных условий имеет вид

(4.23)

Отметим, что для Е-волн в волноводе можно записать E_mn, где индексы m, n определяют конкретную структуру поля. Для Е-волн ни одно из чисел m, n не может быть равно нулю, в противном случае составляющая E_Z=0, следовательно и другие составляющие поля обратятся в нуль. Таким образом, волны Е-типа в прямоугольном волноводе вида Е_0n и E_m0 не существуют.

В таблице 4.1 показана структура поля волн Е- и Н-типа в прямоугольном волноводе, также приведены формулы, определяющие их основные характеристики.

Приведем пример расчета параметров волны, при ее распространении в прямоугольном волноводе .

Прямоугольный волновод, заполненный воздухом, имеет поперечное сечение .

Определить все типы волн, которые могут существовать в волноводе при частоте 5000 МГц. Для основной волны и для волны с наиболее высокими значениями и найти критическую длину волны в волноводе, фазовую и групповую скорости.

Решение.

1. Определяем длину волны в свободном пространстве:

Зная, что скорость света с=310⁸ м/с находим м.

2. Критическую длину волны в волноводе определяем по формуле:

.

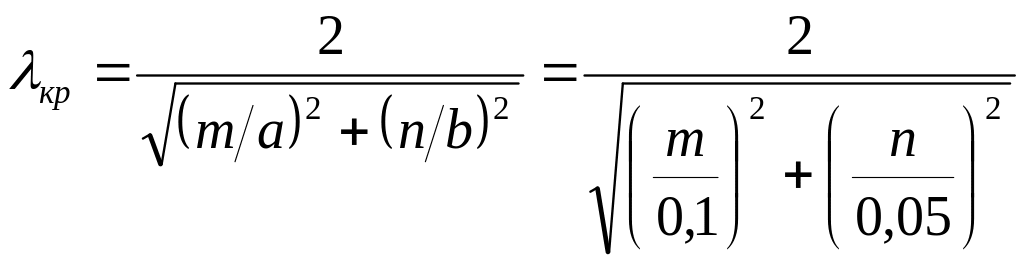По волноводу могут распространяться волны, которые удовлетворяют условию , или в нашем случае

Придавая и целые значения, найдём искомые типы волн. Так, при и получим м, т.е. в волноводе может существовать волна типа . Аналогично определяем, что по волноводу могут распространяться также волны типа и . Других типов волн в волноводе быть не может. Действительно, пусть и . Тогда получим

,

т.е. требуемое неравенство не соблюдается. Для волн типа и находим длину волны в волноводе, её фазовую и групповую скорости. Для волн типа ( или Н₁₀) имеем:

,

,

,

Для волны типа находим: ; , , .

Круглые волноводы