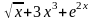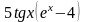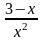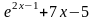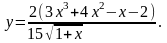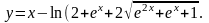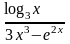Лекция___. Понятие производной. Дифференцирование функции одной переменной

Производная (функции в точке) - основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференцированием. Обратный процесс - интегрирование.

Определение 1. Пусть в некоторой окрестности точки определена функция Производной функции называется такое число , что функцию в окрестности U(x₀) можно представить в виде f(x₀ + h) = f(x₀) + Ah + o(h), если существует.

Определение 2. Пусть в некоторой окрестности точки определена функция Производной функции f в точке x₀ называется предел, если он существует,

Геометрический смысл производной функции в точке - это тангенс угла наклона между осью абсцисс и касательной к графику этой функции, проходящей через точку с абсциссой .

1. Если угол наклона касательной острый, то тангенс положительный, а значит, производная положительна.

2. Если угол наклона касательной тупой, то тангенс отрицательный, а значит, производная отрицательна.

3. Если угол наклона касательной равен нулю, то тангенс равен нулю, а значит, производная равна нулю.

4. Если угол наклона прямой, то тангенс не существует, а значит, производная не существует.

Пример 1

Найти производные следующих постоянных функций

Решение.

В первом случае мы имеем производную натурального числа 3, во втором случае нам приходится брать производную от параметра а, который может быть любым действительным числом, в третьем - производную иррационального числа , в четвертом случае имеем производную нуля (ноль является целым числом), в пятом – производную рациональной дроби .

Ответ: производные всех этих функций равны нулю для любого действительного x (на всей области определения)

Пример 2

Найти производные функций .

Решение.

Первую и третью функцию приведем к табличному виду , используя свойства степени, и применим формулу производной степенной функции:

Пример 3

Найти производные показательных функций

.

Решение.

Воспользуемся доказанной выше формулой производной показательной функции из таблицы и свойствами логарифма.

Пример 4

Вычислить производные логарифмических функций .

Решение.

Формулу мы уже вывели, так давайте ею и воспользуемся (в первом случае основание логарифма равно натуральному логарифму трех a = ln3, во втором a = e):

Пример 5.

Найти производную функции .

Решение.

Из таблицы производных для тригонометрических функций видим . Воспользуемся правилом вынесения множителя за знак производной:

Достаточно часто приходится сначала упрощать вид дифференцируемой функции, чтобы воспользоваться таблицей производных и правилами нахождения производных. Следующие примеры это наглядно подтверждают.

Пример 6

Выполнить дифференцирование функции .

Решение.

По свойствам логарифмической функции можно перейти к записи . Осталось вспомнить производную логарифмической функции и вынести постоянный множитель:

Пример 7

Найти производную функции .

Решение.

Преобразуем исходную функцию .

Применяем правило вынесения множителя за знак производной и из таблицы берем производную показательной функции:

Пример 8.

Найти производную функции .

Решение.

Упростим вид исходной функции

.

Используем правило производной суммы (разности):

В предыдущем пункте мы доказали, что постоянный множитель можно выносить за знак производной, поэтому

Осталось воспользоваться таблицей производных:

Пример 9

Продифференцировать функцию .

Решение.

В данном примере . Применяем правило производной произведения:

Обращаемся к таблице производных основных элементарных функций и получаем ответ:

Пример 10

Найти производную функции .

Решение.

В этом примере . Следовательно,

Пример 11

Найти производную функции .

Решение.

Функция представляет собой разность выражений и , поэтому

В первом выражении выносим двойку за знак производной, а ко второму выражению применяем правило дифференцирования произведения:

Домашнее Задание

Лекция________. Производные высших порядков

Пусть y = f(x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде

Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:

Производные более высокого порядка (если они существуют), определяются как

Для нахождения производных высшего порядка можно использовать следующие формулы:

В частности, для производной второго и третьего порядка формула Лейбница принимает вид

Пример 1

Найти y'', если .

Решение.

Возьмем первую производную, дифференцируя функцию как произведение:

Теперь найдем производную второго порядка:

Пример 2

Вычислить y'' для параболы .

Решение.

Дифференцируя как неявную функцию, имеем

Дифференцируя еще раз и используя правило для производной произведения, получаем Умножим обе части на y² :

Поскольку yy' = 2, и следовательно, (yy' )² = 4, то последнее уравнение записывается в виде: Отсюда следует, что

Пример 3

Найти все производные функции .

Решение.

Пусть u = e ^x и v = x ². Тогда

Легко устанавливаются общие формулы для производных n-порядка:

Используя формулу Лейбница

Получаем

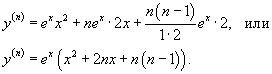
Лекция___. Полное исследование функции и построение ее графика

Задача: провести полное исследование функции и построить ее график .

Алгоритм исследования функции

1. Нахождение области определения функции.

Определение 1. Область определения функции - множество, на котором задаётся функция.

Определение 2. Если задана функция, которая действует из одного множества в другое, то множество, из которого действует данная функция, называется областью определения.

Определение 3. Пусть задано отображение f, которое отображает множество X в Y, то есть: ; тогда

множество X называется областью определения функции f и обозначается D(f), или dom f (от англ. domain «область»).

Правила нахождения области определения функции:

Пусть y=f(x) и y=g(x) - основные элементарные функции или их комбинации.

Для степенных функций вида , где n - четное, область определения находится из системы:

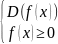
Для логарифмических функций вида область определения находится из системы:

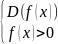
Для дробей вида область определения находится из системы:

Для функций тангенса или котангенса вида tg(f(x)) или ctg(f(x)) область определения находится из систем соответственно:

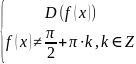или

Для функций арксинус или арккосинус вида arcsin(f(x)) или arccos(f(x)) область определения находится из системы (т.к. областью определения арксинуса и арккосинуса является отрезок от -1 до 1):

Для показательно степенных функций вида вида область определения находится из системы:

Область определения суммы (разности) функций вида находится из системы:

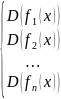
Область определения комбинации рассмотренных выше функций вида находится из системы:

Нужно найти нули знаменателя и исключить их из области действительных чисел.