Вариант 11

1. Точка M(3,2) является основанием перпендикуляра, опущенного из точки N(1,-1) на прямую l. Написать уравнение прямой l; найти расстояние от точки N до прямой l.

2. Даны вершины треугольника A(4,–3), B(7,3), C(1,10).

Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.

3. Даны два вектора ={1,2,5}, ={3,-5,7}. Найти вектор при условии, что он перпендикулярен к оси Oz и удовлетворяет условиям =3, = -2.

4. Дано: В(6,3,3), C(6,4,2), D(4,1,4). Найти:

• площадь треугольника BCD

• высоту треугольника BCD, опущенную из вершины В

Вариант 12

1. Даны точки 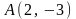, . Через середину отрезка провести прямую, перпендикулярную к . Найти ее угловой коэффициент.

2. Даны вершины треугольника A(4,–4), B(8,2), C(3,8).

Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.

3. Найти вектор , зная, что он перпендикулярен векторам ={3,-2,1} и ={1,2,-3}, и образует острый угол с осью Oy.

4. Дано: А(2,-1,-2), В(1,2,1), C(2,3,4) и D(-5,0,-6). Доказать, что точки A, B, C, D не лежат в одной плоскости. Найти:

• угол между векторами

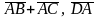
• высоту треугольника ABC, опущенную из точки С

Вариант 13

1. Даны вершины треугольника: , , . Через каждую из них провести прямую, параллельную противоположной стороне.

2. Даны вершины треугольника A(–3,–3), B(5,-7), C(7,7).

Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.

3. Найти вектор , зная, что он коллинеарен вектору ={3,0,4}, образует острый угол с осью Oх.

4. Дано: А(2,-1,-2), В(1,2,4), C(2,3,0) и D(5,0,-6). Показать, что точки A, B, C, D не лежат в одной плоскости. Найти:

• высоту пирамиды ABCD, опущенной из вершины B

• угол между векторами

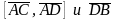
Вариант 14

1. Найти расстояние между параллельными прямыми и .

2. Даны вершины треугольника A(1,–6), B(3,4), C(-3,3).

Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.

3. Подобрать число  так, чтобы векторы , , 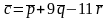были линейно зависимы.

4. Дано: А(1,2,3), В(9,5,4), C(3,0,4) и D(5,2,6). Найти:

• длину высоты пирамиды, проведенной из вершины С

• угол между векторами и осью Oy

Вариант 15

1. Через точку 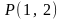провести прямую, отсекающую равные отрезки на осях координат.

2. Даны вершины треугольника A(–4,2), B(8,-6), C(2,6).

Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.

3. Найти единичный вектор , перпендикулярный вектору ={3,-6,-1} и оси Oy и образующий острый угол с осью Оz

4. Дано: А(2,-1,-1), В(5,-1,2), C(3,0,-3) и D(13,-1,-1). Найти:

• высоту пирамиды, опущенную на грань ABC

•