
Вариант 1
Найти угловой коэффициент k прямой, проходящей через точки
 (1,8)
и
(1,8)
и
 (–1,4);
записать уравнение прямой в параметрическом
виде.
(–1,4);
записать уравнение прямой в параметрическом
виде.Даны вершины треугольника A(3,2), B(5,–2), C(1,0).
Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.
Даны векторы
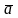 ={2,-1,3},
={2,-1,3},
 ={1,-3,2},
={1,-3,2},
 3i+2j-4k.
Найти вектор
3i+2j-4k.
Найти вектор
 ,
удовлетворяющий условиям
,
удовлетворяющий условиям
 =10,
=10,
 =22,
=22,
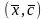 =-40
=-40Дано: А(1,1,2), В(2,3,-1), C(2,-2,4) и D(-1,1,3). Найти:
объем пирамиды ABCD
угол между векторами
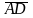 и
и

Вариант 2
Найти острый угол между прямой
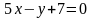 и прямой, проходящей через точки
(–2,3)
и
(2,–3).
и прямой, проходящей через точки
(–2,3)
и
(2,–3).Даны вершины треугольника A(–10,–13), B(–2,3), C(2,1).
Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.
Найти единичный вектор , зная, что он перпендикулярен векторам ={1,-1,3}, ={3,-2,5} и образует с осью Оz тупой угол.
Векторы
 i+mj-2k,
=2j-k
и
{3,-1,2}
образуют правую тройку. Объем
параллелепипеда, построенного на этих
векторах, равен 6 кубическим единицам.
Найти:
i+mj-2k,
=2j-k
и
{3,-1,2}
образуют правую тройку. Объем
параллелепипеда, построенного на этих
векторах, равен 6 кубическим единицам.
Найти:
m
угол между векторами
 и
и

Вариант 3
Записать общее уравнение прямой, проходящей через две точки (–6,4) и (–2,–1). Найти угловой коэффициент этой прямой.
Даны вершины треугольника A(–4,–2), B(–6,6), C(6,2).
Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.
Вектор , перпендикулярный к векторам ={1,1,2}, и =i+k образуют тупой угол с осью Oy. Найти его координаты, зная что

Проверить, лежат ли точки А(1,2,-3), В(0,-1,2), C(3,2,1) и D(0,1,-3) в одной плоскости. Найти:
Площадь треугольника ABC
Высоту пирамиды, проведенную из точки D
Вариант 4
Составить уравнение прямой, если точка A(4,5) служит основанием перпендикуляра, опущенного из начала координат на эту прямую. Найти угловой коэффициент k этой прямой.
Даны вершины треугольника A(–2,–3), B(1,6), C(6,1).
Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.
Даны векторы ={2,1,1}, ={1,3,1}, i+j+5k,
 2i+3j-3k.
Найти вектор
,
удовлетворяющий условиям
=2,
=5,
=-7,
2i+3j-3k.
Найти вектор
,
удовлетворяющий условиям
=2,
=5,
=-7,
 =14
=14Точки А(-2,1,-3), В(3,4,4), C(5,6,0) и D(5,6,е) служат вершинами параллелепипеда, объем которого равен 16 куб. ед. Найти:
а) е
б) высоту параллелепипеда, опущенную из точки D
Вариант 5
Даны две точки (2,3) и (–1,0). Составить уравнение прямой, проходящей через точку перпендикулярно отрезку
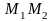 .
Записать уравнение прямой в параметрическом
виде.
.
Записать уравнение прямой в параметрическом
виде.Дан треугольник с вершинами A(–1,2), B(5,7), C(1,–3). Найти: уравнение стороны АВ; уравнение высоты CH; уравнение медианы АМ; точку N пересечения AM и CH; уравнение прямой, проходящей через вершину С параллельно стороне AB.
Найти вектор зная, что он перпендикулярен векторам ={1,-1,3}, ={3,-2,5} и удовлетворяет условию (
 2i-2j-k)=
-7.
2i-2j-k)=
-7.Дано: А(1,1,1), В(2,3,4), C(4,3,2) и D(-4,-3,-2). Найти:
объем пирамиды,
построенной на векторах

площадь
параллелограмма, построенного на
векторах
 и
и

