Тема 8. Матроиды и greedy алгоритмы

Лекция 1. Теорема Радо-Эдмондса

1. Теорема Радо-Эдмондса [1,2,3,4,5,6,7,8,9]

Рассмотрим следующую задачу.

Задача 8.1. Дана матрица с целыми неотрицательными коэффициентами . Требуется найти такое подмножество ее элементов, что: а) в каждом столбце матрицы содержится не более одного элемента из этого подмножества и б) сумма выбранных элементов максимальна.

Эквивалентная формулировка этой задачи, очевидно, имеет вид:

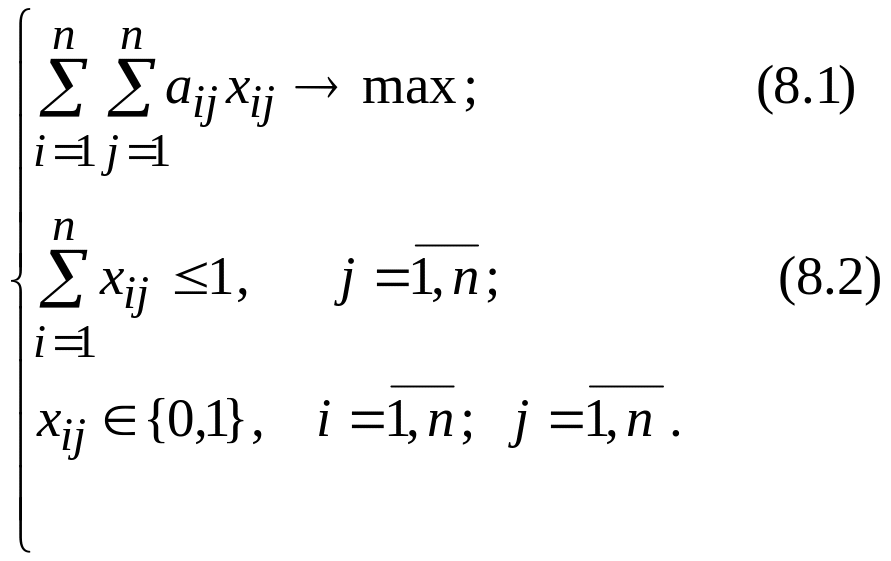
Будем решать задачу 8.1, отбирая последовательно элементы из , причем каждый раз - наибольший из оставшихся невыбранными, проверяя при этом выполнение ограничений (8.2). Алгоритмы такого типа называют жадными или пожирающими (в англоязычной литературе - GREEDY). Жадные алгоритмы похожи на градиентные алгоритмы в численных методах непрерывной математики.

Легко убедиться, что жадный алгоритм правильно решает задачу 9.1. Эта задача является индивидуальной задачей проблемы целочисленного линейного программирования (ЦЛП) с булевыми переменными и ограничениями, задание которых в этом частном случае определяет полиномиальную разрешимость задачи 9.1 со сложностью .

Для примера рассмотрим задачу 8.1 с матрицей

= .

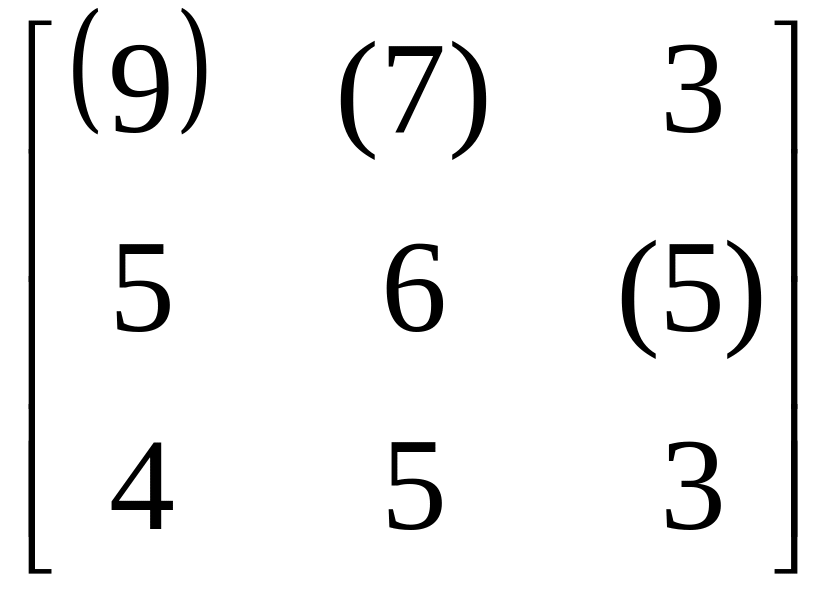Выбор наибольшего элемента в первом столбце в искомое подмножество исключает из дальнейшего рассмотрения (в силу заданного ограничения) элементы . Из второго столбца выбирается и затем - из третьего столбца - . Имеем . Это – точное экстремальное решение задачи. Скобками отмечены отобранные элементы.

Рассмотрим еще один частный случай задачи ЦЛП.

Задача 8.2. Дана матрица с целыми неотрицательными коэффициентами. Найти такое подмножество ее элементов, что а) в каждом столбце и в каждой строке находится не более одного выбранного элемента и б) сумма выбранных элементов является максимальной.

Эквивалентная формулировка задачи:

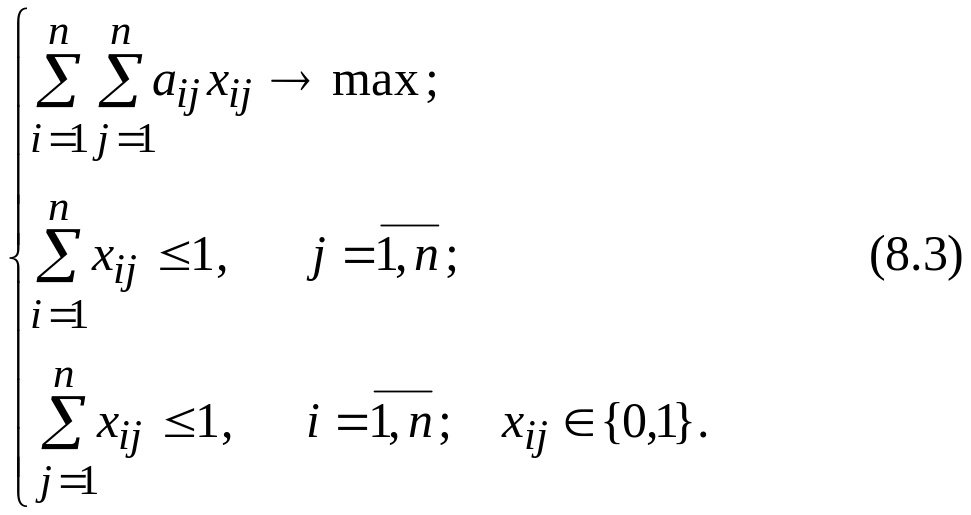
Попробуем применить жадный алгоритм к задаче (8.3) с матрицей

= .

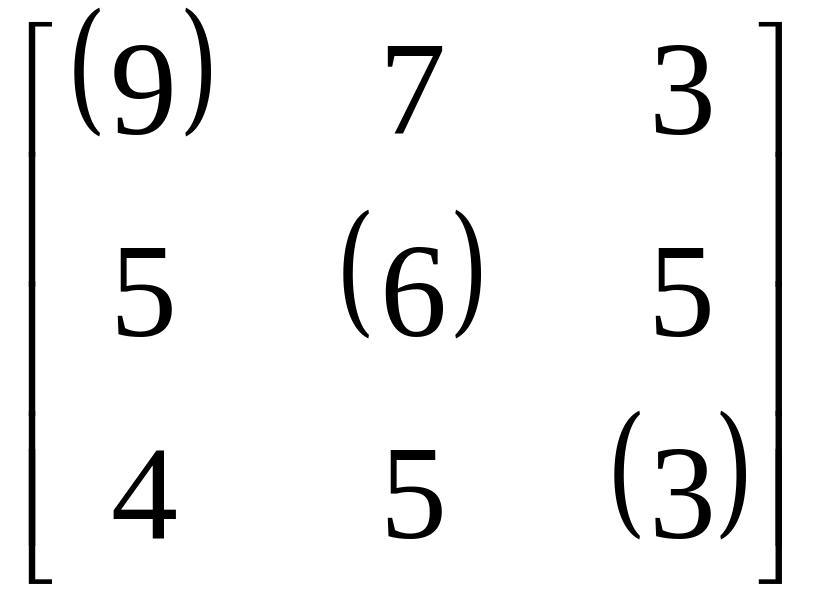Выбор наибольшего элемента в первой строке и столбце в искомое подмножество исключает из дальнейшего рассмотрения (в силу заданных ограничений) элементы . Поэтому из второго столбца выбирается и затем - из третьего столбца - . Имеем . Но это решение не экстремальное: подмножество удовлетворяет ограничениям и . Укажем в матрице элементы экстремального решения:

.

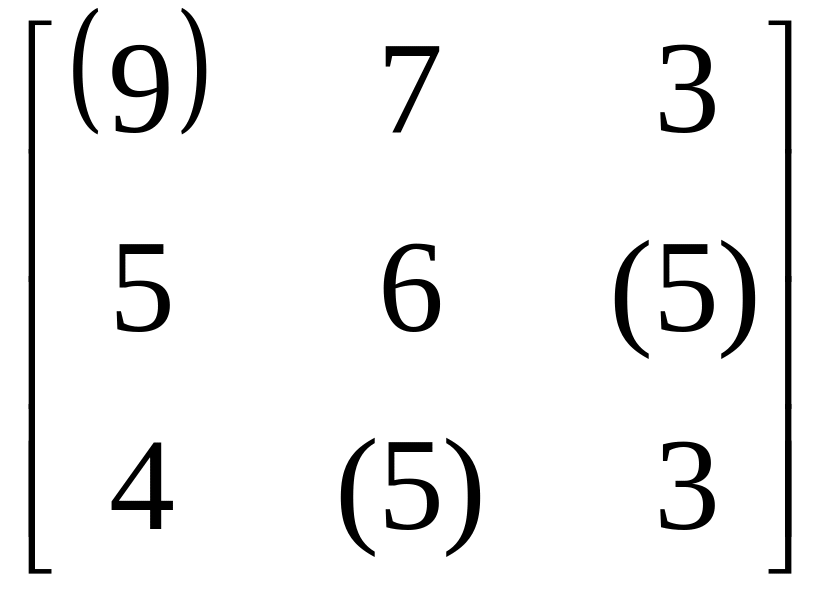Теперь рассмотрим более широкий, общий класс задач, включающий в себя задачи 9.1 и 9.2 .

Задача 9.3. Дано конечное множество Е, семейство его подмножеств ( - булеан множества Е) и функция  : Е  R⁺ . Требуется найти подмножество S J с наибольшей суммой .

Эквивалентная формулировка задачи 8.3:

Значение функции (е) будем называть весом элемента е е. Задача 8.3 может быть переформулирована так: найти допустимое подмножество s j с наибольшим суммарным весом.

Определение 9.1. Жадным (пожирающим, GREEDY) называется следующий алгоритм решения задачи 9.3:

begin

Упорядочить веса элементов так, что

ω(e[1]) >= ω(е[2]) >= ... >= ω (е[n]);

S:=; // Сначала отобранное подмножество пусто

for i := 1 tо n dо // Цикл выбора элементов

if (S  {e[i]})  J then S := S  {е[i]}; // Проверка принадлежности допустимому множеству

еnd.

Замечание. Для упрощения определения GREEDY алгоритма мы, не теряя общности, считаем, что после упорядочения элементов множества Е они получили имена (и номера) е[1], е[2], ... , е[n].

Типичной иллюстрацией частного случая использования GREEDY алгоритма является стратегия «иди в ближайший» для задачи о кратчайшем пути в графе.

Очевидно, что сложность GREEDY алгоритма определяется сложностью задачи сортировки n-элементного множества, которая может быть оценена как О(nlogn), и сложностью n–кратной проверки свойства (S  {e[i]})  J . Если эта проверка реализуема с полиномиальной сложностью, то и GREEDY алгоритм в целом имеет полиномиальную сложность.

Простота GREEDY алгоритма делает его привлекательным и определяет важность постановки следующего вопроса: каким условиям должно удовлетворять семейство J из задачи 9.3, чтобы GREEDY- алгоритм правильно решал эту задачу для произвольной функции ? Оказывается, для решения поставленной проблемы достаточно, чтобы пара <Е,J> образовывала так называемый матроид.

Определение 8.2. Матроидом называется пара М=<Е,J>, где Е - конечное множество. J  2^Е - семейство его подмножеств, удовлетворяющих условиям:

М1) пустое множество принадлежит J и, если А J и В А, то B J;

М2) для любых множеств А и В таких, что А J, B J и В = А + 1 , найдется элемент е В \ А такой, что А{e} J.

Множества семейства J называют независимыми, а остальные множества из {2^E \ J}- зависимыми.

Определение 8.3. Максимальным независимым подмножеством множества СЕ называется такое независимое подмножество А  С, что не существует независимого множества В, удовлетворяющего включениям: А  В  С.

Условия М1) и М2) в определении 8.2 иногда называют аксиомами матроида.

Теорема 8.1. Пусть Е - конечное множество, J  2^Е и J удовлетворяет условию М1. Тогда пара М = <Е,J> является матроидом в том и только том случае, если выполняется условие:

МЗ) для любого подмножества С  Е каждые два максимальных независимых подмножества множества С имеют одинаковую мощность.

Доказательство. Теорема устанавливает равносильность аксиом М2 и МЗ, поэтому в символической записи следует доказать М1М2М3 и М1М3М2.

Докажем М1М2М3. Последнее равносильно тому, что М3М1М2. Если аксиома М3 не выполняется, то для некоторого подмножества С  Е найдутся два максимальных независимых множества и такие, что . Тогда существует множество такое, что , но для любого соотношение не может выполняться, поскольку это противоречит максимальности множества , то есть М2 не выполняется.

Покажем справедливость соотношения М2М1М3. Если не выполняется аксиома М2, то найдутся независимые множества и такие, что , но для любого имеет место . Поэтому - максимальное независимое множество в , и при этом в существует максимальное множество большей мощности. Таковым является либо множество , либо его расширение : , то есть М3 не выполняется.

Определение 8.4. Мощность максимального независимого подмножества множества СЕ называется рангом этого множества С и обозначается r(С).

Определение 8.5. Каждое максимальное независимое подмножество множества Е из определения матроида М = <Е,J> называется базой этого матроида, а ранг r(E) - рангом матроида.

Следствие 8.1. Каждые две базы матроида равномощны.

Теорема 8.2. (Радо-Эдмондса) Если м = <Е,J> - матроид, то множество S, найденное GREEDY- алгоритмом при решении задачи 9.3, является независимым множеством с наибольшим весом . Если М = <Е,J> не является матроидом, то найдется такая функция  : Е  R⁺ , что множество S, найденное GREEDY- алгоритмом, не будет являться множеством с наибольшим весом.

Доказательство. Пусть М = <Е,J> - матроид и - независимое множество, построенное GREEDY- алгоритмом. Тогда . Рассмотрим произвольное независимое множество , элементы которого упорядочены по весу: . S - база матроида, поскольку каждый элемент , не включенный в S на некотором шаге алгоритма, не может пополнить окончательно построенное множество S . Действительно, если на некотором шаге было сформировано независимое множество и затем элемент был отвергнут, как нарушающий условие (S_t  {e_i})  J , то для любого независимого множества такого, что , выполнение условия (А  {e_i})  J означало бы, что (S_t  {e_i}) (А  {e_i}), (А  {e_i})  J, но (S_t  {e_i}) J, что противоречит аксиоме М1 матроида. Тогда, поскольку S - база, должно выполняться соотношение . В этом легко убедиться, если предположить, что . Тогда для двух независимых множеств S и V таких, что , по аксиоме М2 в сужении таком, что , обязан найтись такой элемент , что . А это противоречит тому, что S - база матроида. Для доказательства неравенства , учитывая, что , достаточно показать справедливость соотношения для любого . Предположим противное: для некоторого и рассмотрим два независимых множества и . По аксиоме М2 - независимое множество, если . Тогда имеем Следовательно, существует такой индекс , что . Множество является независимым по аксиоме М1 и имеет больший вес, чем множество . Последнее противоречит тому, что множество выбрано GREEDY- алгоритмом.

Теперь предположим, что М = <Е,J> не является матроидом. Тогда нарушается хотя бы одна из аксиом матроида М1, М2.

Пусть не выполняется М1. Тогда найдутся подмножества А и В такие, что A J ,

B А , но B J . Определим функцию  так:

Множество B J не будет содержаться во множестве S, выбранном жадным алгоритмом. Поэтому (S) < (B) = (A). Тогда S не является множеством с максимальным весом, а таковым является независимое множество A.

Если же не выполняется аксиома М2, то найдутся множества А  J и B  J такие, что А=k , B=k+1, и для любого e{B\A} будет иметь место {A {e}} J. Обозначим р = A  B; Должно выполняться неравенство р<k, поскольку, в противном случае, если р=k, то , и тогда для любого e{B\A} должно выполняться {A {e}} J. Определим функцию  так:

(e)=

Тогда жадный алгоритм сначала выберет все элементы множества А, затем во всех случаях отбросит элементы множества B\A. Будет получено множество S с весом (S) = (A) = k(1+ε). Найдем вес независимого множества B, которое, очевидно, не может быть отобрано жадным алгоритмом: (B) = p(1+ ε) +(k+1- p) ·1 = k + pε + 1. Если (B)>(A), то GREEDY- алгоритм находит решение, не являющееся оптимальным. Последнее имеет место при выполнении неравенства k + pε + 1 > k+ kε, равносильного условию .

Таким образом, мы установили, что если в задаче 8.3 множество допустимых решений J является семейством независимых множеств матроида <Е,J> , то эта задача точно решается GREEDY-алгоритмом.

Литература:

1. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. – 416 с.

2. Ахо А., Хопкрофт Д., Ульман Д. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979. – 536 с.

3. Грэхем Р., Кнут Д., Паташник О. Конкретная математика (основание информатики). М.: Мир, 1998. – 703 с.

4. Донской В. И. Дискретная математика. –Симферополь: Сонат, 2000. –356 с.

5. Липский В. Комбинаторика для программистов. М.: Мир, 1988. – 215 с.

6. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Физико-математическая литература, 1995. – 256 с

7. Линдон Р. Заметки по логике. М.: Мир, 1968. – 128 с.

8. Оре О. Теория графов. М.: Наука, 1980. – 336 с.

9. Шоломов Л. А. Основы теории дискретных логических и вычислительных устройств. М.: Наука, 1980. – 400 с.

Лекция 2. Виды матроидов

1. Графовые матроиды [1,2,3,4,5,6,7,8,9]

Графовый матроид строится на основе задания конечного графа. В качестве множества берется множество ребер графа , и рассматриваются такие подмножества ребер , что подграф не содержит циклов.

Теорема. Пусть - конечный граф; - множество вершин, - множество ребер графа ; - такая совокупность подмножеств множества ребер графа , что для любого граф не содержит циклов. Тогда - матроид.

Доказательство. Вспомним, что граф, не содержащий циклов, является деревом (если он связный, это означает существование для любой его пары вершин соединяющего их пути) или, в противном случае, лесом, состоящим из конечного числа деревьев – компонент связности. Используя метод математической индукции, легко показать, что любое дерево, содержащее вершин, имеет ровно ребер. Если лес содержит компонент связности с числом вершин соответственно : , то этот лес имеет ровно ребер. Рассмотрим любое максимальное подмножество ребер в произвольном множестве такое, что граф не содержит циклов. Если граф связен, то - дерево, и мощность максимального множества определяется соотношением . Если граф не связен и имеет компонент связности, то - лес, и тогда мощность максимального множества есть . Таким образом, мощности любых максимальных множеств в произвольного множества равны, что обеспечивает выполнение для пары условия М2.

Легко убедиться, что и условие М1 выполняется для системы . Поскольку пустое подмножество ребер определяет граф с изолированными вершинами, имеем . И если граф не содержит циклов, то и любой его подграф такой, что не будет содержать циклов, поэтому .□

Матроид , удовлетворяющий условию теоремы, называют графовым.

Практическая полезность понятия графового матроида становится очевидной при рассмотрении алгоритма Краскала решения задачи о кратчайшем стягивающем лесе.

Задача 9.4(о кратчайшем стягивающем лесе).

Дан конечный граф с заданными значениями функции стоимости ребер. Требуется построить граф , , такой, чтобы он не содержал циклов и оставался связным на любом подмножестве вершин, которые образуют связный подграф графа , и при этом условии суммарная стоимость ребер множества была бы минимальной. Иначе говоря, требуется отобрать максимальное множество ребер так, чтобы (в общем случае) лес не содержал циклов, а суммарная стоимость этих ребер была бы минимальной.

Следующий Алгоритм Краскала позволяет точно решить эту задачу нахождения максимального по включению множества ребер, не образующих цикл и имеющего минимальную суммарную стоимость в силу выполнения условий на множестве допустимых решений, определяющих графовый матроид (см. доказательство теоремы).

Обозначим - вершины и - ребра графа .

Упорядочить ребра по стоимости: .

// После упорядочения, не теряя общности, считаем, что последовательность

// индексов отсортированных элементов есть 1,2,…,n.

; // Начальное разбиение

// на одноэлементные подмножества.

; // Множество отобранных ребер сначала пусто.

for i:=1 to m do // Оно пополняется, если граф не имеет циклов.

if then

begin

; // Добавление ребра.

; // Укрупнение разбиения.

end;

В приведенном алгоритме ребра пополняют множество до тех пор, пока множество не образует цикл графа, или, если цикла не окажется, пока не будут добавлены все ребра множества . Это – вариант жадного алгоритма (хотя аддитивная целевая функция минимизируется, а не максимизируется). Множество - разбиение – в процессе выполнения алгоритма содержит изменяющееся, но не превышающее число элементов. На каждом шаге цикла проверяется, принадлежат ли концы очередного ребра различным элементам разбиения, на что потребуются временные затраты, очевидно, ограниченные оценкой . Такую же оценку имеет сложность выполнения слияния элементов разбиения (шаг укрупнения разбиения). Поэтому сложность алгоритма Краскала можно оценить, по крайней мере, как , включая предварительную сортировку. Следовательно, алгоритм Краскала является полиномиальным. Точное решение гарантируется теоремой Радо-Эдмондса: множество допустимых решений задачи является совокупностью подмножеств ребер исходного графа, не образующих циклов, иначе говоря, системой множеств, образующей с исходным множеством ребер графовый матроид.

2. Матричные матроиды [1,2,3,4,5,6,7,8,9]

3. Линейная независимость над полем GF(2) и матроиды [1,2,3,4,5,6,7,8,9]

Литература:

1. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. – 416 с.

2. Ахо А., Хопкрофт Д., Ульман Д. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979. – 536 с.

3. Грэхем Р., Кнут Д., Паташник О. Конкретная математика (основание информатики). М.: Мир, 1998. – 703 с.

4. Донской В. И. Дискретная математика. –Симферополь: Сонат, 2000. –356 с.

5. Липский В. Комбинаторика для программистов. М.: Мир, 1988. – 215 с.

6. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Физико-математическая литература, 1995. – 256 с

7. Линдон Р. Заметки по логике. М.: Мир, 1968. – 128 с.

8. Оре О. Теория графов. М.: Наука, 1980. – 336 с.

9. Шоломов Л. А. Основы теории дискретных логических и вычислительных устройств. М.: Наука, 1980. – 400 с.

Лекция 3. GREEDY алгориттмы

1) Примеры успешной работы GREEDY алгоритмов

Литература:

10. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. – 416 с.

11. Ахо А., Хопкрофт Д., Ульман Д. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979. – 536 с.

12. Грэхем Р., Кнут Д., Паташник О. Конкретная математика (основание информатики). М.: Мир, 1998. – 703 с.

13. Донской В. И. Дискретная математика. –Симферополь: Сонат, 2000. –356 с.

14. Липский В. Комбинаторика для программистов. М.: Мир, 1988. – 215 с.

15. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Физико-математическая литература, 1995. – 256 с

16. Линдон Р. Заметки по логике. М.: Мир, 1968. – 128 с.

17. Оре О. Теория графов. М.: Наука, 1980. – 336 с.

18. Шоломов Л. А. Основы теории дискретных логических и вычислительных устройств. М.: Наука, 1980. – 400 с.

Преподаватель Донской В.И. подпись