Министерство образования и науки, молодежи и спорта Украины

Таврический национальный университет

им. В.И. Вернадского

Кафедра дифференциальных уравнений и геометрии

Методические указания и задания

по изучению курса

«Дифференциальные уравнения»

для студентов 2-го курса дневной и заочной

форм обучения специальностей

6.040201 «Математика», 6.040302 «информатика»,

6.040301 «Прикладная математика»

образовательно-квалификационного уровня «бакалавр»

Симферополь 2011

Печатается по решению научно-методического совета Таврического национального университета им. В.И. Вернадского.

Темы курса (I часть):

• Дифференциальные уравнения первого порядка. Интегральные кривые. Поле направлений. Дифференциальные уравнения первого порядка с разделяющимися переменными.

• Однородные уравнения первого порядка. Уравнения приводящиеся к однородным.

• Линейные дифференциальные уравнения первого порядка. Метод вариации произвольных постоянных. Уравнения Бернулли. Уравнения Риккати.

• Дифференциальные уравнения в полных дифференциалах и приводящиеся к ним.

• Дифференциальные уравнения неразрешенные относительно производной. Уравнения Лагранжа и Клеро.

• Дифференциальные уравнения высших порядков. Дифференциальные уравнения, допускающие понижения порядка.

• Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами. Характеристическое уравнение. Случай простых корней. Комплексные корни. Кратные корни. Фундаментальная система решений.

• Линейные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью.

• Линейные неоднородные дифференциальные уравнения высших порядков. Общее решение. Метод вариации произвольных постоянных.

• Уравнения Эйлера.

1. Дифференциальные уравнения в прикладных задачах

1.1. Дифференциальные уравнения физики, механики

Решение физической задачи реальной жизни должно последовательно проходить в три этапа:

• составление дифференциального уравнения;

• решение этого уравнения;

• исследование полученного решения.

При этом рекомендуется следующая последовательность действий:

1. Установить величины, изменяющиеся в данном явлении, и выявить физические законы, связывающие их.

2. Выбрать независимую переменную и функцию этой искомой переменной.

3. Исходя из условий задачи, определить начальные или краевые условия.

4. Выразить все фигурирующие в условии задачи величины через независимую переменную, искомую функцию и производные этой функции.

5. Исходя из условий задачи и физического закона, которому подчиняется данное явление, составить дифференциальное уравнение.

6. Найти общее решение или общий интеграл дифференциального уравнения.

7. По начальным или краевым условиям найти частное решение.

8. Исследовать полученное решение.

Во многих случаях составление дифференциального уравнения основывается на так называемой «линейности процесса в малом», т. е. на дифференцируемости функций, выражающих зависимость величин. Как правило, можно считать, что все участвующие в том или ином процессе величины в течение малого промежутка времени изменяются с постоянной скоростью. Это позволяет применить известные из физики законы, описывающие равномерно протекающие явления, для составления соотношения между значениями , т. е. между величинами, участвующими в процессе, и их приращениями. Получающееся равенство имеет лишь приближённый характер, поскольку величины меняются даже за короткий промежуток времени, вообще говоря, неравномерно. Но, если разделить обе части получившегося равенства на и перейти к пределу, когда , получится точное равенство. Оно содержит время меняющиеся с течением времени физические величины и их производные, т. е. является дифференциальным уравнением, описывающим данное явление. То же самое уравнение в дифференциальной форме можно получить, заменив приращение на дифференциал , а приращение функций - соответствующими дифференциалами.

Таким образом, при составлении дифференциального уравнения мы делаем как бы «мгновенный снимок» процесса в данный момент времени, а при решении уравнения по мгновенным снимкам восстанавливаем течение процесса. Общая идея замены функций на малых промежутках аргумента линейными функциями, лежащая в основе решения физических задач с помощью дифференциальных уравнений, называется линеаризацией.

И хотя встречаются процессы, для которых линеаризация невозможна (например, броуновское движение), описываемый метод в подавляющем большинстве случаев действует безотказно.

Задача 1.1. Материальная точка массы замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости . Найти зависимость скорости от времени. Найти скорость точки через с после начала замедления, если м/с, а м/с.

Решение. Примем за независимую переменную время , отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки будет функцией , т. е. . Для нахождения воспользуемся вторым законом Ньютона (основным законом механики): , где - есть ускорение движущегося тела, - результирующая сила, действующая на тело в процессе движения. В данном случае , - коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция является решением дифференциального уравнения

или .

Здесь - масса тела.

Отсюда,

,

где .

Найдя зависимость скорости от времени, легко найти скорость точки через 3 c после начала замедления.

Найдем сначала параметры и . Согласно условию задачи, имеем:

и .

Отсюда, , . Следовательно, скорость точки изменяется по закону .Поэтому м/с.

Ответ. Скорость точки через 3 с после начала замедления 25 м/с.

Задача 1.2. Пусть на тело массы , подвешенное к концу пружины, действует возвращающая сила, пропорциональная величине растяжения пружины. Пусть – величина отклонения тела от положения равновесия. Тогда по второму закону Ньютона, который утверждает, что ускорение (вторая производная от по времени, обозначаемая ) пропорционально силе:

.

Правая часть стоит со знаком минус потому, что возвращающая сила уменьшает растяжение пружины.

Задача 1.3. Закон охлаждения тел утверждает, что количество тепла в теле убывает пропорционально разности температур тела и окружающей среды. Если чашка кофе, разогретого до температуры 90° С находится в помещении, температура в котором равна 20° С, то

,

где – температура кофе в момент времени .

Задача 1.4. В дне цилиндрического сосуда, наполненного водой и имеющего высоту и радиус основания , сделано небольшое отверстие площади (Рисунок 1.1). За какой промежуток времени через отверстие вытечет вся вода, если треть воды вытекает за секунд?

Рисунок 1.1. Графическое изображение обозначений

Решение. Если бы истечение воды происходило равномерно, то решение задачи было бы тривиальным: вся вода вытечет за время c. Но, реально, сначала вода вытекает быстро, а по мере снижения уровня воды в сосуде скорость её истечения уменьшается. Таким образом, необходимо учесть зависимость между скоростью истечения и высотой столба жидкости над отверстием. Опыты Торричелли показали, что скорость приближённо выражается формулой , где – ускорение свободного падения и – «безразмерный» коэффициент, зависящий от вязкости среды и формы отверстия (для воды в случае круглого отверстия ).

Сделаем «мгновенный снимок» процесса истечения жидкости за промежуток времени . Пусть в начале этого промежутка высота жидкости над отверстием равнялась , а в конце его она понизилась и стала , где – «приращение» высоты (которое, очевидно, отрицательно). Тогда объём жидкости, вытекшей из сосуда, равен объёму цилиндра с высотой и площадью основания .

Эта жидкость вылилась в виде цилиндрической струйки, имеющей площадь основания . Её высота равна пути, пройденному вытекающей из сосуда жидкостью за промежуток времени .

В начале этого промежутка времени скорость истечения равнялась по закону Торричелли,

,

а в конце его она равнялась

.

Если весьма мало, то и тоже очень мало и потому полученные выражения для скорости практически одинаковы, а путь, пройденный за промежуток времени , выражается формулой:

,

где

т. е

–

объём вылившейся из сосуда за промежуток времени жидкости.

Приравнивая два выражения для объёма жидкости, вылившейся из сосуда за промежуток времени , получаем уравнение:

. (1.1)

Недостатком уравнения (1.1) является то, что нам не известно выражение для . Для устранения этого недостатка, разделим обе части уравнения (1.1) на и перейдём к пределу при . Учитывая, что , а .

Получаем дифференциальное уравнение:

. (1.2)

Для решения уравнения (1.2), разделим переменные и обозначим для краткости дробь через :

.

Получаем уравнение

.

Интегрируя обе части, получаем:

. (1.3)

Мы получили зависимость между и , в которую входят две постоянные и . Постоянная зависит от размеров и формы отверстия, вязкости жидкости и других физических параметров, а постоянная возникла в ходе решения задачи. Их значения нам не известны, но их можно найти, учтя не использованные ещё условия задачи.

Для нахождения используем начальные условия: в начале истечения жидкости сосуд был наполнен, т. е. при высота .

Подставляя в формулу (1.3) , получаем:

.

Равенство (1.3) можно переписать в виде:

.

Для нахождения , учтём, что за первые минут вытекла треть всей жидкости. Этому соответствует понижение уровня жидкости на . Иными словами, при имеем: . Отсюда находим, что:

,

и потому,

. (1.4)

Теперь уже не трудно найти время опорожнения сосуда, т.е. найти такое значение , при котором :

.

Заметим, что хотя последнее значение примерно в 1,82 раз больше значения , которое получилось в предположении, что жидкость вытекает равномерно, оно не является безукоризненно точным, так как мы пренебрегли, например, явлениями капиллярности (существенными при малом диаметре отверстия), завихрениями жидкости, пограничным слоем жидкости и многими иными факторами.

Исследуем полученное решение. Подставим в равенство (1.4) значение найденного и получим, что:

,

.

Ясно, что, чем больше значения и (размеры сосуда), тем дольше будет вытекать из него жидкость, как это и следует из полученного ответа. Чем больше площадь отверстия , тем быстрее вытечет жидкость из сосуда. В том же направлении действует и увеличение ускорения , а так же коэффициента (чем больше , тем больше скорость истечения жидкости в формуле Бернулли).

Таким образом, формула выдержала «испытание на здравый смысл», что в совокупности с испытанием на размерность: подтверждает, что задача решена верно.

Ответ. Вся вода вытечет через отверстие за промежуток времени

.

Во многих случаях составление дифференциальных уравнений по условию задачи облегчается тем, что соответствующий закон физики связывает между собой значение некоторой величины и скорости её изменения, либо связывает друг с другом значения величины, скорости её изменения и ускорения.

Задача 1.5. Исследование полета снаряда.

Рассмотрим, что происходит со снарядом после того, как он покинет канал ствола.

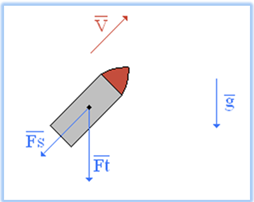
Рисунок 1.2. Снаряд, вылетевший из канала ствола.

На снаряд, вылетевший из канала ствола, действуют две силы:

• сила земного притяжения, которая зависит от величины массы снаряда – силы тяжести снаряда;

• сила сопротивления воздуха.

Сила тяжести направлена вертикально вниз и постепенно снижает траекторию снаряда. Воздушная среда оказывает сопротивление движению снаряда, отражающееся на его скорости.

Причины, вызывающие появление силы сопротивления:

• снаряд при движении раздвигает частицы воздуха, следовательно, часть его энергии расходуется на преодоление сил сцепления частиц воздуха;

• при движении снаряда часть его энергии расходуется на приведение в движение частиц воздуха впереди головной части снаряда;

• частицы воздуха во время движения снаряда скользят по его поверхности; при этом возникает сила трения, на преодоление которой тоже расходуется часть энергии снаряда;

• позади снаряда во время ее движения получается разреженное пространство, увеличивающее силу сопротивления воздуха.

Совокупность влияний на снаряд перечисленных факторов составляет силу сопротивления воздуха, действующую на снаряд во время полёта.

Сила сопротивления воздуха зависит от скорости полета снаряда, от его формы, массы, калибра, поверхности, плотности воздуха.

От увеличения плотности воздуха, калибра снаряда и ее скорости сопротивление воздуха возрастает, а чем глаже поверхность пули, тем меньше сила трения и сила сопротивления воздуха. Для нарезного оружия, имеющего сверхзвуковые скорости, у снарядов оптимальной формой является форма с удлиненной головной частью, а форма хвостовой части не имеет значения. При дозвуковой скорости целесообразно иметь удлиненную хвостовую часть, сужающуюся к концу. Рассмотрим теперь, как ведет себя снаряд при полете в воздушном пространстве. Введем два понятия – равнодействующую всех сил, образующих сил сопротивления воздуха, и точку ее приложения к пуле – центр сопротивления. Если бы пуля двигалась все время головной частью вперед, то сила сопротивления была бы направлена по оси пули от головной ее части к хвостовой. Такой случай на практике будет, когда пуля выстрелена вертикально вверх.

Продолговатый невращающийся снаряд при вылете из канала ствола под действием вылетающих вслед за ним газов, получив от них толчок, будет двигаться так, что его ось несколько отклонится от направления движения (от касательной к траектории). В результате одна сторона окажется более подверженной силе сопротивления воздуха, чем другая. Так как центр сопротивления лежит впереди центра тяжести, то снаряд будет опрокидываться. Чтобы избежать этого, ему придают вращение с помощью нарезов. В этом случае происходит следующее. Сила сопротивления воздуха стремится повернуть снаряд головной частью вверх и назад. Но головная часть снаряда в результате быстрого вращения отклонится не вверх, а весьма незначительно в сторону своего вращения под прямым углом к направлению действия силы сопротивления воздуха, т.е. вправо. Как только головная часть снаряда отклонится вправо, изменится направление силы сопротивления воздуха – она стремится повернуть головную часть снаряда вправо и назад, но поворот головной части снаряда произойдет не вправо, а вниз и т. д. Так как действие силы сопротивления воздуха непрерывно, а направление ее относительно снаряда меняется с каждым отклонением оси пули, то головная часть снаряда описывает окружность, а его ось – конус вокруг касательной к траектории с вершиной в центре тяжести, и пуля летит головной частью вперед. В результате вращательного движения пули и действия на нее силы сопротивления воздуха и силы тяжести происходит отклонение пули от плоскости стрельбы в сторону ее вращения. Отклонение пули от плоскости стрельбы в сторону ее вращения называется деривацией.

Исследования траектории пули в воздухе показывают:

• восходящая ветвь траектории длиннее и отложе нисходящей ветви;

• угол падения больше угла бросания;

• скорость пули в точке падения меньше начальной;

• наименьшая скорость полета пули при стрельбе под большими углами бросания – на нисходящей ветви траектории, а при стрельбе под небольшими углами бросания – в точке падения;

• угол наибольшей дальности меньше 45°;

• время движения пули по восходящей ветви меньше времени движения по нисходящей ветви траектории;

• траектория вращающейся пули под действием силы тяжести и деривации представляет собой линию двоякой крутизны. В плоскости стрельбы имеет две ветви и первую крутизну, при виде сверху (в плане), в силу деривации – отлогую кривую, обращенную выпуклостью в сторону к плоскости стрельбы.

Аналитическое решение. Идеализация модели:

1. Земля плоская.

2. Не учитываем возможное влияние ветра.

3. Считаем значения плотности воздуха и ускорения свободного падения не зависящими от высоты.

4. Не учитываем вращение снаряда в полете, а следовательно и деривацию.

Переменные:

,

где

– масса снаряда,

– его начальная скорость,

– ее проекции,

– угол бросания (угол возвышения орудия),

– ускорение свободного падения,

– сила сопротивления воздуха,

– сила тяжести,

– аэродинамический (баллистический) коэффициент,

– площадь поперечного сечения снаряда,

– плотность воздуха.

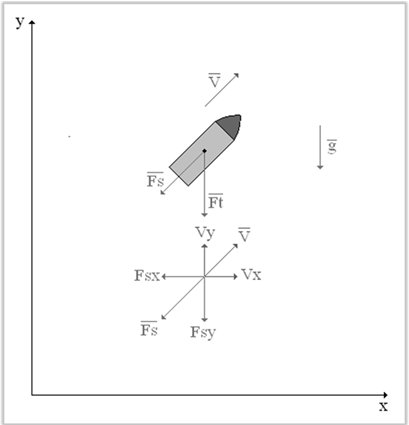
Рисунок 1.3

Уравнения связи.

Напишем второй закон Ньютона для нашего снаряда:

.

Распишем:

.

То же самое в проекциях на и :

,

.

Распишем силы:

,

причем знак «минус» показывает что вектор силы (и ускорения) направлен противоположно вектору скорости.

.

Подставим их в проекции:

,

,

причем знак «минус» перед появился из-за того, что направлен вверх, а – вниз.

Поделив на , получим выражения для проекций ускорения:

,

.

Или:

,

.

Учтем что:

,

.

Получим:

,

.

Возьмем интеграл для составляющей :

,

,

,

,

,

.

Взятие интеграла для составляющей аналогично, но полученное выражение будет отличаться от выражения для на величину

:

.