3 Силовой анализ рычажного механизма
3.1 Исходные данные
3.1.1 План механизма в расчетном положении
Рисунок 3.1 –схема механизма в расчетном положении
3.1.2 Величина силы полезного сопротивления:
.
3.1.3 Удельная масса звеньев q = 30 кг/м.
3.2 Определение активных силовых факторов и инерционной нагрузки на звенья
3.2.1 Находим массы звеньев:
кг;
кг;
кг.
Массу ползуна 5 считаем равной массе шатуна 4: m5 = m4 = 25,8 кг.
3.2.2 Силы веса звеньев:
H;
Н;
Н;
Н.
3.2.3 Силы инерции звеньев:
Н;
Н;
Н;
Н.
3.2.4 Вычисляем моменты инерции звеньев относительно их центров масс:
кг·м2;
кг·м2;
кг·м2.
3.2.5 Моменты пар сил инерции, действующие на звенья:
Н·м;
Н·м;
Н·м.
3.2.6 Поскольку кривошип 1 считаем сбалансированным, аs1 = 0 и Fu1 = 0. В связи с тем, что ω1 – const, ε1 = 0 и Mu1 = 0. Силой веса кривошипа пренебрегаем ввиду малости.
3.2.7 Наносим на план механизма найденные активные силовые факторы. Инерционную нагрузку направляем при этом противоположно соответствующим ускорениям.
3.2.8 Наносим также векторы уравновешивающей силы Fу и силы полезного сопротивления Fпс.
3.2.9 Находим величину перемещения выходного звена 5 в расчетном положении, то есть при φр = 115°:
м.
3.2.10 Вычисляем значение силы полезного сопротивления в расчетном положении:
Н.
3.3 Силовой расчет структурной группы 4 – 5
3.3.1 В масштабе μl = 0,01 м/мм вычерчиваем план этой группы и наносим на него активные силовые факторы, а также реакции связей от соседних звеньев.
3.3.2 Составляем векторное уравнение равновесия и проводим его анализ:
В уравнении 3 неизвестные величины, у которых известно только направлении действия.
3.3.3 Для нахождения одной "лишней" неизвестной составляем и решаем уравнение моментов относительно точки D:
.
3.3.4 Решение векторное уравнение графически. С этой целью в масштабе μF = 12,5 Н/мм откладываем все известные векторы, а затем проводим известные направления двух искомых векторов. Длины векторов:
мм;
мм;
мм;
мм;
мм;
мм.
3.3.5 Определяем неизвестные реакции:
Н;
Н;
Н.
3.4 Силовой расчет структурной группы 2 – 3
3.4.1 В масштабе μl = 0,01 м/мм строим план группы и наносим действующие силовые факторы.
3.4.2 Векторное уравнение равновесия:
3.4.3 Для каждого звена составляем уравнение моментов относительно центра шарнира В и находим тангенциальные составляющие реакций.
Для
звена 2:
.
Для
звена 3:
3.4.4 Используя масштабный коэффициент μF = 12,5 Н/мм, решаем векторное уравнение графически. Длины векторов:
мм;
мм;
мм;
мм;
мм;
мм;
мм.
Из плана находим полные реакции:
Н;
Н;
Н;
Н.
3.5 СИЛОВОЙ РАСЧЕТ ВХОДНОГО ЗВЕНА
3.5.1 В масштабе μl = 0,005 м/мм вычерчиваем план звена и наносим на него все действующие силовые факторы.
3.5.2 Векторное уравнение равновесия:
.
3.5.3 В масштабе μF = 2,5 Н/мм решаем уравнение графически:
мм.
3.5.4 Из плана механизма находим:
Н;
Н.
4 СИНТЕЗ И КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЗУБЧАТОГО МЕХАНИЗМА
4.1 ИСХОДНЫЕ ДАННЫЕ
4.1.1 Кинематическая схема механизма
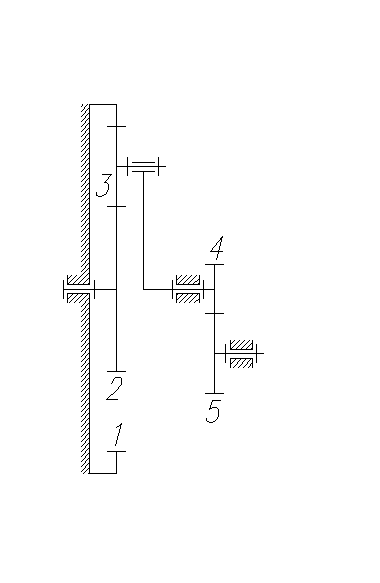
z1 = ?; z2 = 37; z3 = 18; z4 = 11; z5 = 18.
Рисунок 4.1 – Кинематическая схема механизма
4.1.2
Величина угловой скорости выходного
вала
рад/с (по пункту 2.1.2).
4.1.3 Направление вращения выходного вала по часовой стрелке (по пункту 1.4).
4.2 ОПРЕДЕЛЕНИЕ НЕИЗВЕСТНОГО ЧИСЛА ЗУБЬЕВ ОДНОГО ИЗ КОЛЕС
4.2.1 Вычисляем подвижность механизма:
,
где п = 4 – число подвижных звеньев;
рz = 3 – количество зубчатых зацеплений.
.
В механизме одно входное звено и для него может быть вычислено передаточное отношение.
4.2.2 Устанавливаем, что рассматриваемый механизм состоит из двух ступеней: обычной (колеса 4 и 5 неподвижны оси вращаются) и планетарный (колеса 1, 2, 3 и водило Н).
4.2.3 Условие соосности для планетарной части:
;
.
4.2.4 Неизвестное число зубьев колеса 2:
.