2 Кинематический анализ рычажного механизма

2.1 Исходные данные

2.1.1 Кинематическая схема механизма

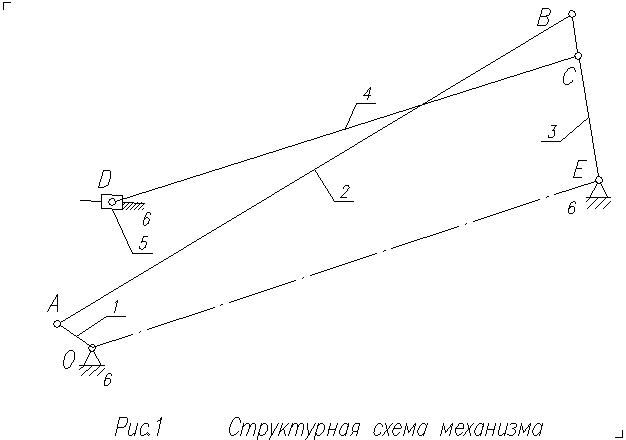
Размеры звеньев: l_OA = 0,12 м; l_AB = 1,72 м; l_BE = 0,48 м; l_CD = 0,86 м; l_EC =0,36 м.

Рисунок 2.1 – Кинематическая схема

2.1.2 Величина угловой скорости кривошипа ω_К = 13,2 рад/с.

2.1.3 Направление вращения кривошипа – против часовой стрелки.

2.1.4 Угол поворота кривошипа в расчетном положении φ_п = 115° от положения, соответствующего началу рабочего хода в сторону вращения.

2.1.5 Закон изменения силы полезного сопротивления:

,

где = 1,8 – максимальное значение силы F_пс.

h – ход выходного звена.

S – перемещение выходного звена в расчетном положении.

2.2 ПОСТРОЕНИЯ ПЛАНА МЕХАНИЗМА В РАСЧЕТНОМ ПОЛОЖЕНИИ

2.2.1 Приняв масштабный коэффициент плана μ_l = 0,005 м/мм, вычисляем длины отрезков на плане, соответствующих звеньям механизма:

мм;

мм;

мм;

мм;

мм;

мм;

мм.

2.2.2 Изображаем элементы стойки: шарниры О и Е, а также направляющую MD под углом β = 20°.

2.2.3 Вычерчиваем кривошип OA под углом φ_p = 115° к межосевой линии OE.

2.2.4 Из точки E проводим дугу окружности радиуса = 96 мм (траектория точки B).

2.2.5 С помощью программы AutoCAD на прямой = 344 мм делаем засечку на траектории точки B и находим эту точку.

2.2.6 Проводим прямые и .

2.2.7 Строим стержень = 72 мм.

2.2.8 С помощью программы AutoCAD на прямой = 366 мм делаем засечку на направляющей стойки и находим центр шарнира D.

2.2.9 Соединяем точки C и D прямой линией, изображаем ползун.

2.2.10 Проставляем обозначения кинематических пар, номера звеньев, углы поворота кривошипа φ_р и коромысла γ, а также направления вращения кривошипа.

2.2.11 Определяем длину хода выходного звена в расчетном положении:

м.

2.3 Определение линейных и угловых скоростей

2.3.1 Вычисляем скорость центра шарнира A:

м/с.

2.3.2 Рассматривая плоское движение звена 2, составляем векторное уравнение скорости центра шарнира B и анализируем входящие в него величины:

.

2.3.3 Исходя из ориентировочной длины вектора V_A = 160 мм, находим приближенное значение масштабного коэффициента плана скоростей:

м/(с·мм).

2.3.4 Принимаем стандартное значение μ_V = 0,01 м/(с·мм).

2.3.5 Решаем векторное уравнение графически. Длина вектора, известного полностью:

мм.

Искомые линейные скорости:

м/с;

м/с.

2.3.6 Используя теорему о подобии, строим на плане точку с.

,

откуда

мм,

2.3.7 Составляем, анализируем и решаем векторное уравнение для скорости точки D:

.

Искомые линейные скорости:

м/с;

м/с.

2.3.8 Угловые скорости звеньев:

рад/с;

рад/с;

рад/с.

2.3.9 Определяем направления угловых скоростей и проставляем их на плане механизма.

2.4 Определение линейных и угловых ускорений

2.4.1 Вычисляем ускорение точки А. Поскольку ω₁ – const, оно является полностью нормальным:

м/с².

2.4.2 Рассматривая плоское движение звена 2 и вращательное звена 3, составляем систему векторных уравнений ускорения точки В и анализируем входящие в них величины:

,

.

2.4.3 Вычисляем нормальные составляющие ускорений:

м/с²;

м/с².

2.4.4 Аналогично п. п. 2.3.3 и 2.3.4 определяем масштабный коэффициент плана ускорений. Принимаем μ_a = 0,1 м/(с²·мм).

2.4.5 Решаем систему графически. Для этого из каждого уравнения сначала откладываем полностью известные векторы, а затем проводим известные направления до их пересечения в точке b. Длины векторов на плане:

мм;

мм;

мм.

Поскольку а_Е = 0, точка е совпадает с полюсом π.

2.4.6 Аналогично п. 2.3.6 строим на плане точку с.

;

мм.

Определяем ускорение точек B и C:

м/с²;

м/с².

2.4.7 Составляем, анализируем и решаем векторное уравнение ускорения точки D:

,

где м/с².

Тогда мм.

Тангенциальные составляющие ускорений:

м/с²;

м/с²;

м/с².

Ускорение точки D:

м/с².

Ускорение звена CD:

м/с².

2.4.8 Определяем угловые ускорения звеньев:

рад/с²;

рад/с²;

рад/с².

Наносим их направления на план механизма.

2.4.9 Находим ускорения центров масс звеньев. Считаем, что они лежат на их серединах. Используем при этом теорему о подобии для каждого из звеньев:

м/с²;

м/с²;

м/с².