25 Исходные данные

25.1 Кинематическая схема

Числа зубьев: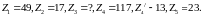

Рисунок 8 - Кинематическая схема механизма

25.2 Угловая скорость выходного вала:

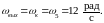
25.3 Направление вращения по часовой стрелке (см. п. 4.4).

26 Определение неизвестного числа зубьев одного из колёс

26.1 Выделяем из механизма планетарную часть: сателлит 2 сцепляется од­новременно с колесом 1 и сателлитом 3, сателлит 3 имеет зацепление с колесом 4. Оси вращения колес 1 и 4 совпадают с осью вращения водила Н, т.е. 1 и 4 –централь­ные колеса. Т. е. 3, 2 и 1, 4 – планетарная часть. 4´, 5 – непланетарная часть. Т.к. одно из центральных колес (колесо 1) неподвижно, механизм обладает одной степе­нью свободы. Проверим это расчетом:

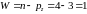
26.2 Условие соосности для планетарной части:

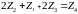
26.3 Неизвестное число зубьев колеса :

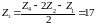
27 Кинематический расчет механизма аналитическим методом

27.1 Передаточное отношение не планетарной части механизма

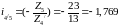
27.2 В планетарной ступени требуется записать передаточное отношение от подвижного центрального колеса к водилу:

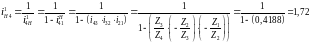
27.3 Передаточное отношение всего механизма

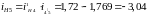
27.4 Ввиду того, что

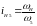
угловая скорость водила

-звена 4

27.6 Далее используем метод инверсии. Угловые скорости центральных колес при остановленном водиле:

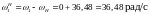
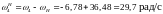
27.7 Передаточное отношение от центральных колес к сопряженным с ними сателлитами:

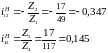
27.8 Угловые скорости сателлитов относительно водила:

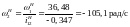
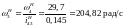
27.9 Угловые скорости сателлитов относительно стойки:

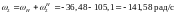
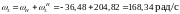
Сателлит 2 вращается в ту же сторону, что и колесо 1 (знаки угловых скоростей совпадают), а сателлит 3- в противоположную (знаки различны).

Задача аналитическим методом решена.

28 Кинематический расчет механизма графическим методом

28.1 Предположив, что модуль колес m=5 мм, вычисляем радиусы их дели­тельных окружностей:

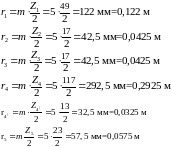
28.2 Вычерчиваем механизм с масштабным коэффициентом μ_l=0,005 м/мм, обозначаем центры колёс, а также точки их контакта. Проводим вспомогательную линию и проецируем на неё упомянутые точки.

28.3 Окружная скорость точки водила:

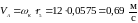
Принимаем μ_v=0,02 м/(с·мм)

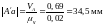
28.4 Построение планов линейных скоростей звеньев выполняем в следую­щей последовательности.

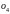- через точки и проводим прямую длиной 41,4 мм

- через точки и - прямую 4 до т.С

- через точки 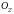и - прямую Н до пересечения с прямой 4

- через точк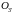и и 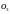- прямую до пересечения с прямой Н

- через точки 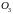и - прямую до т.b

- через точки b и -прямую до точки a

- через точки и a проводим прямую, ограниченную точками и a.

28.5 Строим картину частот вращения. Приняв , вычисля­ем длину полюсного расстояния:

.

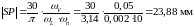28.6 Проводим из точки P наклонные прямые, параллельные планам скоро­стей звеньев, и измерив соответствующие отрезки, находим искомые величины частот вращения. Те из них, которые совпадают по направлению с 1, считаем по­ложительными, остальные – отрицательными:

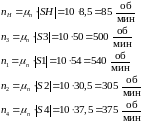
28.7 Сопоставляем значения частот вращения, определённых графически с вычисленными аналитически. Относительная погрешность:

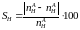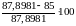%= %=3,297%‹5%

%

%

%

%
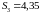
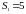
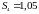