Синтез зубчатого зацепления

4. ИСХОДНЫЕ ДАННЫЕ

4.1 Число зубьев колес z₁ = 13 и z₂ = 25.

4.2 Модуль зацепления m = 8 мм .

4.3 Критерии качества

– Коэффициент торцевого перекрытия ε 

– Коэффициент удельного скольжения зубьев колеса и шестерни должны быть равны

– Подрез зубьев шестерни и колеса не разрешается

5. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СМЕЩЕНИЯ

5.1 Исходя из заданных чисел зубьев z₁ = 13 и z₂ = 25 по ближайшему бло­кирующему контуру для z₁ = 13 и z₂ = 25 выбираем коэффициенты смещения таким образом, чтобы обеспечить равенство удельных скольжений λ₁ = λ₂, величину коэф­фициента перекрытия ε ≥ 1,2 и толщину зуба шестерни на окружности вершин S_a ≥ 0,25 m. Принимаем предварительно x₁´= 0,6 ; x₂´= 0,5 .

5.2 Инволюта угла зацепления:

Угол зацепления α _w ≈ 26º 29´.

5.3 Предварительное межосевое расстояние:

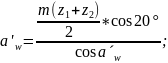
5.4 Округляем межосевое расстояние до ближайшего значение из ряда нормальных линейных размеров = 160 мм .

5.5 Уточняем угол зацепления:

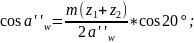
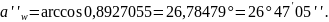
5.6 Сумма коэффициентов смещения:

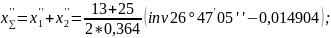
5.7 По блокирующему контору с учетом (…) распределяем 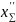по колесам. Принимаем Используя блокирующий контур, распределяем найденное значение по колесам. При этом принимаем такие значения и которые обеспечивают выполнение условий, перечисленных в п. 18.1. Этим требованиям соответствует точка с коорди­натами X₁ = 0,33 и X₂ = 0,1 .

5.8 Радиусы начальных окружностей:

r_w1 =( а_w / (z₁ + z₂ )) ∙ z₁ = (92 / 36) ∙ 13 = 33,22 мм;

r_w2 =( а_w / (z₁ + z₂ )) ∙ z₂ = (92 / 36) ∙ 23 = 58,77 мм.

Проверка:

а_w = 33,22 + 58,77 = 92 мм.

5.9 Радиусы делительных окружностей:

r₁ = m ∙ z₁ / 2 = 5 ∙ 13 / 2 = 32,5 мм;

r₂ = m ∙ z₂ / 2 = 5 ∙ 23 / 2 = 57,5 мм .

22.11 Радиусы основных окружностей:

r_b1 = r₁ ∙ cos 20º = 32,5 ∙ 0,94 = 30,55 мм;

r_b2 = r₂ ∙ cos 20º = 57,5 ∙ 0,94 = 54,05 мм.

22.12 Радиусы окружностей впадин:

r_f1 = r₁ + m ∙( X₁ – 1,25) = 32,5 + 5 ∙ (0,33 – 1,25) = 27,9 мм ;

r_f2 = r₂ + m ∙( X₂ – 1,25) = 57,5 + 5 ∙ (0,1 – 1,25) = 51,75 мм .

22.13 Радиусы окружностей вершин:

r_a1 = α_w – r_f2 – 0,25 ∙ m = 92 – 51,75 – 0,25 ∙ 5 = 39 мм ;

r_a2 = α_w – r_f1 – 0,25 ∙ m = 92 – 27,9 – 0,25 ∙ 5 = 62,85 мм .

22.14 Шаг по делительной окружности:

p = π ∙ m = 3,14 ∙ 5 = 15,7 мм .

22.15 Угловые шаги:

τ₁ = 360º / z₁ = 360º / 13 = 27,69º ;

τ₂ = 360º / z₂ = 360º / 23 = 15,65º .

22.16 Вычисляем размеры зубьев :

- высоты головок

h_a1 = r_a1 – r₁ =39 – 32,5 = 6,5 мм ;

h_a2 = r_a2 – r₂ =62,85 – 57,5 = 5,35 мм ;

- высоты ножек

h_f1 = r₁ – r_f1 = 32,5 –27,9 = 4,6 мм ;

h_f2 = r₂ – r_f2 = 57,5 –51,75 = 5,75 мм ;

- высоты зубьев

h₁ = h_a1 + h_f1 = 6,5 + 4,6 = 11,1 мм ;

h₂ = h_a2 + h_f2 = 5,35 + 5,75 = 11,1 мм ;

Проверка

h₁ = h₂

- толщины зубьев по делительным окружностям

S₁ = 0,5 ∙ p + 2 ∙ X₁ ∙ m ∙tg 20º = 0,5 ∙ 15,7 + 2 ∙ 0,33 ∙ 5 ∙ 0,364 = 9,051 мм ;

S₂ = 0,5 ∙ p + 2 ∙ X₂ ∙ m ∙tg 20º = 0,5 ∙ 15,7 + 2 ∙ 0,1 ∙ 5 ∙ 0,364 = 8,214 мм .

22.17 Проверяем правильность расчетов радиальных размеров через высоту зубьев:

-коэффициент воспринимаемого смещения

-коэффициент уравнительного смещения

-высоты зубьев

мм.

Результат совпал с п. 18.16.Расчеты выполнены верно.

22.18 Толщина зубьев шестерни по окружности вершин:

S_a1 = r_a1 ∙ ((S₁ / r₁) + 2 ∙ inv 20º – 2 ∙ inv α_a1) ,

где

α_a1 = arccos( r_b1 / r_a1) = arccos (30,55 /39) = 38,43º = 38º26´ ;

S_a1 = 39 ∙ ((9,051 / 32,5) + 2 ∙ 0,014904 – 2 ∙0,12275) = 2,449 мм .

22.19 Проверяем отсутствие заострения зубьев шестерни:

S_a1 / m = 2,449 / 5 = 0,4898 > 0,2

22.20 Длина теоретической линии зацепления:

g = α_w ∙sin α_w = 92 ∙ sin 23,12º = 36,215 мм .

22.21 Размеры общих нормалей.

где

мм,

мм.

23. Вычисление ожидаемых качественных показателей.

23.1 Определяем значение предаточного числа:

.

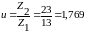2. Вычисляем удельные скольжения колес по формулам:

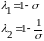
где ρ_k1 – радиус кривизны профиля шестерни в рассматриваемой точке контакта,

.

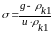Результаты вычислений сводим в таблицу.

Таблица 7

ρk1,мм	0	5	10	15	20	25	30	36,215
		3,529	1,4819	0,7995	0,4583	0,2535	0,117	0
	-	-2,529	-0,4819	0,2005	0,5417	0,7465	0,883	1
	1	0,7166	0,3252	-0,2507	-1,1819	-2,94	-7,539	-

23.3 Коэффициент торцевого перекрытия

23.4 Вычисляем величины коэффициента удельного давления в различных точках теоретической линии зацепления.

Таблица 8.

	0	5	10	15	20	25	30	36,215
ν	5	1,16	0,69	0,569	0,558	0,645	0,971	5

В полюсе зацепления.

.

24 Построение картины зацепления

24.1 Принимаем масштаб ЕСКД М5:1.

24.2 Из. центров O₁ и O₂. расположенных на расстоянии а_w друг от друга для каждого из колес проводим основную, делитель­ную и начальную окружности, а также окружности вершин и впадин.

24.3 На межцентровой линии в точке касания начальных окружностей отмечаем полюс зацепления W и проводим через него об­щую касатель­ную к основным окружностям. Наносим на нее точки N₁ и N₂ – границы теоретиче­ской линии зацепления.

24.4 Строим приближенно эвольвентные профили, сопрягаемые в т. W так, как описано в [3. с. 49–53].

24.5 Строим оси симметрии зубьев, сопрягаемых в полюсе. Для этого на де­лительных окружностях делаем засечки на расстояниях 0,5S от только что постро­енных профилей и проводим оси симметрии зубьев.

24.6 На расстоянии р =15,7 мм по делительной окружности проводим оси симметрии двух соседних зубьев.

24.7 Вырезав шаблоны, вычерчиваем по ним симметричные про­фили зубьев, сопрягаемых в полюсе, а затем и профили соседних зубьев.

24.8 Строим закругления ножек зубьев во впадинах радиусом

.

24.9 Отмечаем границы активной части линии зацепления.

24.10 Выделяем рабочие поверхности профилей зубьев.

24.11 Строим графики удельных скольжений и коэффициента удельного давления( ).

24.12 Проставляем стандартные обозначения размеров. Их чис­ленные значе­ния для обоих колес размещаем в таблице.

ρk1,мм	0	5	10	15	20	25	30	36,215
| |	-	-50,58	-9,36	4,01	10,834	14,93	17,66	20
| |	20	14,332	6,5	-5,014	-23,638	-58,8	-151	-

Таблица 7

	0	5	10	15	20	25	30	36,215
|ν|	100	23,2	13,8	11,38	11,16	12,9	19,42	100

24.13 Строим углы торцевого перекрытия, обозначаем их на картине зацепле­ния и измеряем величины

24.14 Вычисляем коэффициент перекрытия, используя только что измерен­ные значения углов. Сравниваем его с вычисленным в п. 23.3

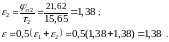
Относительная погрешность:

СИНТЕЗ И КИНЕМАТИЧЕСКИЙ РАСЧЁТ ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ