
Порядок выполнения работы
Всю лабораторную работу можно разбить на 4 этапа:
Этап 1. Экспериментальное определение статических характеристик объекта по каналам регулирования и возмущения.
Этап 2. Математическая обработка результатов экспериментов с целью получения математической модели (уравнения) статики объекта управления в линейном приближении.
Этап 3. Оценка границ применимости линеаризованной математической модели (уравнения) статики двухканального объекта управления.
Этап 4. Оформление отчёта по лабораторной работе (домашнее задание).
Этап 1. Экспериментальное определение статических характеристик
объекта по каналам регулирования и возмущения
1.1. Снять статическую характеристику по каналу регулирования при условии, что Xвоз0=const (конкретное значение помогает определить преподаватель), для чего изменять Xрег в полном диапазоне т.е. от 0 до 100% с шагом 10% при прямом ходе (т.е. при изменении входной величины в сторону увеличения) и при обратном ходе (т.е. при изменении входной величины в сторону уменьшения). В установившихся режимах списывать значения выходной величины объекта (уровня) из окна результатов в заготовленную заранее таблицу №1 экспериментальных данных. (Обратить внимание на то, что все входные и выходные величины виртуального объекта управления в программе ТАУ- 2000 измеряются в условных единицах, а именно, в процентах %).
1.2. Повторить пункт 1 задания при условии, что возмущающее воздействие уменьшилось по сравнению с базовым значением Xвоз0, например на 10%. Результаты записывать в таблицу №1.
1.3. Повторить пункт 1 задания при условии, что возмущающее воздействие увеличилось по сравнению с базовым значением Xвоз0, также например на 10%. Результаты записывать в таблицу №1.
1.4. По данным таблицы №1 построить семейство из трёх статических характеристик объекта по каналу регулирования в координатах Xрег - Xвых (Xрег по оси абсцисс, Xвых по оси ординат), полученных при трёх различных постоянных значениях Xвоз=const (графики желательно строить на миллиметровке для повышения точности построения). Обратить внимание на взаимное расположение характеристик друг по отношению к другу.
Таблица №1
Исследование влияния Хрег на Хвых при трёх различных постоянных значениях Хвоз = const |
|||||||
Хвоз0 = … (например, Хвоз0 = 30%) |
Хвоз= (например, Хвоз= 20%) |
Хвоз = … (например, Хвоз= 40%) |
|||||
Прямой ход |
Обратный ход |
Прямой ход |
Прямой ход |
||||
Хрег % |
Хвых % |
Хрег % |
Хвых % |
Хрег % |
Хвых % |
Хрег % |
Хвых % |
10 |
|
100 |
|
10 |
|
10 |
|
20 |
|
90 |
|
20 |
|
20 |
|
… |
|
…. |
|
|
|
|
|
… |
|
|
|
|
|
|
|
100 |
|
10 |
|
100 |
|
100 |
|
Снять статическую характеристику по каналу возмущения при условии, что Xрег0=const (конкретное значение этой параметра, выбрать с построенного графика статических характеристик канала регулирования с помощью преподавателя, который определит заданный режим работы данного объекта). Здесь необходимо изменять Xвоз в полном диапазоне, т.е. от 0 до 100% и в установившихся режимах записывать значения выходной величины объекта (уровня) в таблицу №2. Значения Хвых снимать только при прямом ходе.
Таблица №2
Исследование влияния Хвоз на Хвых при трёх различных постоянных значениях Хрег0 = const =….. |
|
Хвоз % |
Хвых % |
10 |
|
20 |
|
… |
|
… |
|
100 |
|
1.6. Построить статическую характеристику объекта по каналу возмущения в координатах Xвоз - Xвых при Xрег0=const (желательно на миллиметровке для повышения точности построения и в своей системе координат, т.е. не совмещая со статическими характеристиками по каналу регулирования);
Этап 2. Математическая обработка результатов экспериментов
с целью получения математической модели (уравнения) статики
объекта управления в линейном приближении
2.1. Провести графическую линеаризацию статических характеристик в малой окрестности заданного преподавателем статического режима Xвых0=const путём проведения касательных к статическим характеристикам в точке, соответствующей заданному статическому режиму.
2.2.
Определить коэффициенты усиления
линеаризованных статических характеристик
по каналам регулирования и возмущения,
как тангенсы углов их наклона к оси
абсцисс (т.е. исходя из геометрического
смысла коэффициента усиления) Таким
образом, К1
- коэффициент усиления (передачи) по
каналу регулирования, будет определяться
как К1
=
tg![]() ,
а К2
– коэффициент усиления (передачи) по
каналу возмущения, как К2
=
tg
,
а К2
– коэффициент усиления (передачи) по
каналу возмущения, как К2
=
tg![]() .
.
2.3. Перенести начало координат в точку заданного статического режима и записать уравнения статики в приращениях (в отклонениях) переменных для каждого канала отдельно, как уравнения прямых, проходящих через начало координат:
![]() (1)
(1)
![]() (2)
(2)
2.4. Получить общее уравнение статики двухканального линеаризованного объекта управления, применяя принцип суперпозиции, т.е. складывая воздействия входных сигналов (возмущающего и регулирующего) на выходную величину:
![]() (3)
(3)
Этап 3. Оценка границ применимости линеаризованной математической модели статики двухканального объекта управления
Оценку границ применимости линеаризованных математических моделей (уравнений) статики двухканального объекта управления необходимо провести двумя способами:
1. Визуально по графикам статических характеристик;
2. Путём сравнения результатов специально проведённого эксперимента с результатами расчётов по линеаризованному уравнению статики.
3.1. В результате визуальной оценки в отчёте указать, до каких отклонений входных величин (т.е. возмущающего и регулирующего воздействия) от заданного статического режима наблюдается (на ваш взгляд) достаточно хорошее совпадение реальной (т.е. полученной экспериментально) статической характеристики по каждому каналу с линеаризованной характеристикой (т.е. с касательной).
3.2. Для количественной оценки границ применимости линеаризованных моделей статики необходимо провести специальный эксперимент, смысл которого заключается в следующем. Необходимо одновременно изменять возмущающее и регулирующее воздействия, задавая разные величины их отклонений от заданного статического режима (минимум 3-4 раза). После наступления нового статического режима списывать из окна результатов в таблицу № 3 значения Xвых, рассчитать величину отклонений Xвых от заданного значения по формуле Хвых = Хвых-Хвых0 , результаты записывать в таблицу №3. При тех же значениях отклонений возмущающего и регулирующего воздействий, при которых проводился последний блок экспериментов, рассчитать отклонения выходной величины по полученному линеаризованному уравнению статики (3), результаты расчётов также записать в таблицу №3. Сравнивая экспериментальные и расчётные значения Хвых, оценить совпадение результатов и по ним границы применимости линеаризованного уравнения статики.
Таблица №3
Значения одновременно изменяемых входных величин объекта управления |
Экспериментальные значения Хвых в статике (из окна результатов) |
Отклонения
|
Отклонения , вычисляемые по урав- нению (3) |
Выводы о совпадении результатов экспериментов и расчётов |
||||
|
|
|
|
|||||
+5 |
+5 |
|
|
|
|
|
|
|
-5 |
-5 |
|
|
|
|
|
|
|
+10 |
+10 |
|
|
|
|
|
|
|
-10 |
-10 |
|
|
|
|
|
|
|
+15 |
+15 |
|
|
|
|
|
|
|
-15 |
-15 |
|
|
|
|
|
|
|
Этап 4. Оформление отчёта по лабораторной работе
(домашнее задание)
Отчет по лабораторной работе оформляется один на бригаду в соответствии с требованиями стандартов СТО-2005 и СТО-2006 и сдаётся преподавателю на проверку на следующей лабораторной работе.
Отчет должен включать в себя следующее:
Номер лабораторной работы, её название, цель работы.
Схему исследуемого объекта (принципиальную и структурную) и её краткое описание.
Номер варианта и значения параметров объекта управления, выданные преподавателем.
Параметры заданного статического режима.
Постановку задачи на каждом этапе исследования.
Таблицы экспериментальных данных.
Графики статических характеристик объекта по двум каналам и определённые по ним коэффициенты усиления (передачи) каналов.
Линеаризованные уравнения статики в отклонениях по каждому каналу.
Общее линеаризованное уравнение статики двухканального объекта.
Оценку границ применимости линеаризованной модели статики.

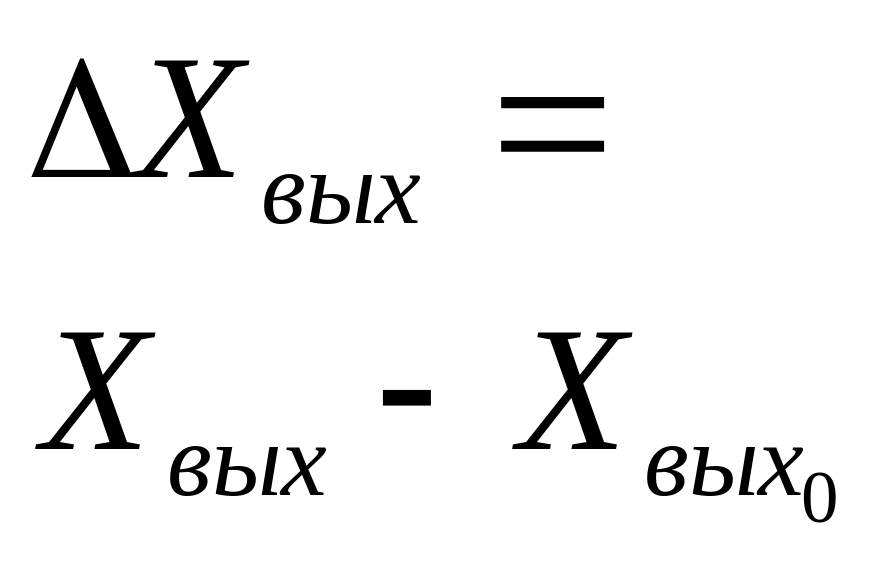 по
экспериментальным данным
по
экспериментальным данным