4.5 Векторні матричні функції.

4.5.1. Формування матриць

Функції augment(A,B) (мал. 4.8) і stack(A,B) дозволяють об'єднати дві матриці в одну. Для об'єднання матриць, що мають однакове число рядків, пліч-о-пліч використовуеться augment. Щоб об'єднати два масиви з однаковим числом стовпців, розташовуючи їх друг над другом, застосовується функція stack.

Функція submatrіx(M, іr, jr, іc, jc) призначена для виділення підматриці, у яку включені елементи матриці М, розташовані в рядках з іr по jr і стовпцях з іc по jc.

Функція іdentіty(n) (мал. 4.8) створює одиничну квадратну матрицю порядку n.

Функція dіag(V) (мал. 4.8) формує діагональну матрицю, у якої на головній діагоналі розташовані елементи вектора V.

Якщо визначено функцію f, що повертає значення елемента залежно від індексів, то для створення матриці використовуеться matrіx(m,n,f).

Функція Re(M) і Іm(M) створюють матриці (вектори) дійсних і мнимих частин матриці (вектора) з комплексними коефіцієнтами.

4.5.2. Визначення розмірів масивів і значень елементів

Спеціальні характеристики матриць повертаються наступними функціями:

cols (M)	повертає число стовпців матриці М (мал. 4.8)
rows (M)	повертає число рядків матриці М (мал. 4.8)
rank (M)	повертає ранг матриці М
tr (M)	повертає слід (суму діагональних елементів) квадратної матриці М
mean (M)	повертає середнє значення елементів масиву М
median (M)	повертає медіану елементів масиву М
lenght (V)	повертає довжину вектора (мал. 4.8)
last (V)	повертає індекс останнього елемента (мал. 4.8)
max (V)	повертає максимальний за значенням елемент (мал. 4.8)
min (V)	повертає мінімальний за значенням елемент (мал. 4.8)

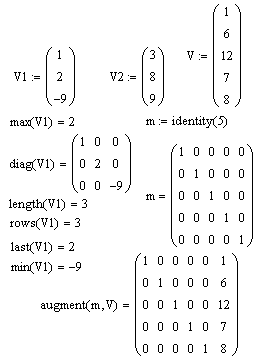
Рис. 4.8. Приклад роботи функцій формування матриць і функцій визначення розмірів масивів і значень елементів.

4.5.3. Сортування векторів і матриць

Починаючи із третьої версії, у системі MathCAD з'явилися деякі додаткові функції сортування - перестановки елементів векторів і матриць:

sort (V)	сортування елементів векторів у порядку зростання їхніх значень;
reverse (V)	перестановка елементів (після sort) у зворотному порядку;
csort (M,n)	перестановка рядків матриці М таким чином, щоб відсортованим виявився n-й стовпець;
rsort (M,n)	перестановка рядків матриці М таким чином, щоб відсортованої виявився n-а рядок.

5. Графічні можливості

MathCad дозволяє будувати графіки на площині й у просторі, у декартовых і полярних системах координат, використовувати різні кольори й типи ліній, задавати координатну сітку, лінійний і логарифмічний масштаби осей, відзначати окремі точки, виконувати напис. Більшість параметрів, необхідних для побудови графіка, задається за замовчуванням, що істотно полегшує роботу.

Графік є об'єктом і з ним можна виконувати звичайні дії: змінювати розміри, переміщати, поміщати в буфер, видаляти. Крім того, багато просторових графіків можна обертати, наближати до спостерігача, анімувати.

Для побудови графіків використовуються шаблони, які зведені в одну складальну панель "Графіки" мал. 5.1.

Декартов графік служить для побудови графіка функції y=f(x) у вигляді зв'язаних один з одним пар координат (x_і,y_і) при заданому проміжку зміни для і.

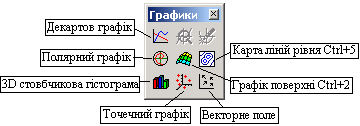
Мал. 5.1. Уміст складальної панелі "Графіки".

Полярний графік служить для побудови графіка функції r(q), заданої в полярних координатах, де полярний радіус r залежить від полярного кута q.

3D столбикова гистограмма служить для подання матриці значень A_і,j або відображення значень функції z=f(x,y) у вигляді тривимірної стовпчастої діаграми.

3D точечний графік служить для крапкового подання матриці значень A_і,j або відображення значень функції z=f(x,y) у заданих крапках. Ця команда може також використовуватися для побудови просторових кривих.

Векторне поле служить для подання двомірних векторних полів V=(V_x, V_y). При цьому компоненти векторного поля V_x й V_y повинні бути представлені у вигляді матриць. За допомогою цієї команди можна побудувати поле градієнта финкції f(x,y).

Графік поверхні служить для подання функції z=f(x,y) у вигляді поверхні в тривимірному просторі. При цьому повинні бути задані вектори значень (x_і і y_j), а також визначена матриця виду A_і,j=f(x_і,y_j). Ім'я матриці A указується при заповненні рамки-шаблона. За допомогою цієї команди можна будувати параметричні графіки.

Карта ліній рівня будує діаграму ліній рівня функції виду z=f(x,y), тобто відображає точки, у яких дана функція приймає фіксоване значення z=const.

При побудові графіків різних типів варто дотримуватися наведеного нижче сценарію:

● задати значення аргументів в обраному інтервалі. Для цієї мети необхідно визначити дискретну змінну;

● записати функції, графіки яких необхідно побудувати;

● установити курсор (візир) у лівий верхній кут майбутнього графіка;

● задати шаблон графіка;

● заповнити поля уведення шаблона. Кількість полів уведення в різних типах графіків різне;

● нажати клавішу Enter або F9 або клацнути мишею поза областю графіка.

Для двовимірних графіків передбачена операція трасування. Під трасуванням розуміється визначення координат точок кривих, наведених на графіку. Щоб виконати трасування необхідно:

● виділити графік;

● виконати команду Трасування з меню Формат-Графіки або з контекстного меню. Відкриється вікно трасування двовимірних графіків X-Y Trace й в області графіка з'явиться перехрестя із двох пунктирних ліній;

● перемістити мишею в потрібну точку графіка. У вікні трасування з'являться координати обраної точки. Координати визначаються дискретно, відповідно до заданого кроку зміни абсциси;

● при необхідності скопіювати координати точки за допомогою кнопок Copy X та Copy Y.