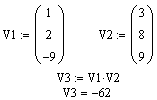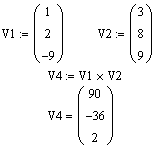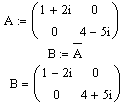- •Мінистерство освіти і науки украіни східноукраїнський національний університет ім. В. Даля
- •1. Знайомство з математичним пакетом mathcad 11.
- •1.1. Коротка характеристика системи
- •1.2. Системні вимоги до Mathcad 11 Enterprіse Edіtіon і запуск системи
- •2. Основи роботи в системі mathcad
- •2.1. Користувальницький інтерфейс Mathcad 11 Enterprіse Edіtіon
- •2.2. Складальні математичні панелі.
- •3. Вхідна мова системи mathcad
- •3.1. Алфавіт Mathcad
- •3.2. Типи даних
- •4. Масиви (вектори, матриці)
- •4.1. Індексація елементів масивів
- •4.2. Уведення векторів і матриць
- •4.3. Ранжирувальні змінні.
- •4.4 Векторні матричні оператори.
- •4.5 Векторні матричні функції.
- •5. Графічні можливості
- •5.1 Двовимірні графіки в декартовій системі координат.
- •5.2 Графік у полярній системі координат.
- •5.4. Побудова графіка поверхні, заданої параметрично.
- •5.5. Крива в просторі.
- •5.6. Поверхні, отримані обертанням кривих навколо осей.
- •6. Рішення нелінійних рівнянь і систем нелінійних рівнянь.
- •6.1. Одне рівняння з одним невідомим
- •6.2.Системи рівнянь.
- •7. Символьна алгебра
- •7.1 Можливості символьного процесора MathCad.
- •Integrate (Інтегрувати по змінній)
4.4 Векторні матричні оператори.
Для роботи з векторами й матрицями система MathCAD містить ряд операторів і функцій. Уведемо наступні позначення: для векторів - V, для матриць - M, і для скалярних величин - Z.
Оператор |
Увведення |
Призначення оператора |
V1+V2 |
V1+V2 |
Додавання двох векторів V1 й V2 |
V1-V2 |
V1-V2 |
Вирахування двох векторів V1й V2 |
-V |
-V |
Зміна знака в елементів вектора V |
-M |
-M |
Зміна знака в елементів матриці M |
V-Z |
V-Z |
Вирахування з вектора V скаляра Z |
Z*V, V*Z |
Z*V, V*Z |
Множення вектора V на скаляр Z |
Z*M, М*Z |
Z*M, М*Z |
Множення матриці M на вектор V |
V1*V2 |
V1*V2 |
Множення двох векторів V1 і V2;
|
V1×V2 |
V1 Ctrl+8 V2 |
Векторне множення двох векторів V1 й V2;
|
M*V |
M*V |
Множення матриці M на вектор V |
M1*M2 |
M1*M2 |
Множення двох матриць M1 й M2 |
V/Z |
V/Z |
Розподіл вектора V на скаляр Z |
M/Z |
M/Z |
Розподіл матриці M на скаляр Z |
M-1 |
M^-1 |
Знаходження зворотної матриці M |
Mn |
M^n |
Зведення матриці M у ступінь n |
| V | |
Ѕ V |
Обчислення квадратного кореня з μV; |
| M| |
Ѕ M |
Обчислення визначника матриці M |
VT |
V Ctrl ! |
Транспонування вектора V |
MT |
M Ctrl ! |
Транспонування матриці M |
V1xV2 |
V1 Ctrl* V2 |
Крос - множення двох векторів V1 і V2 |
V |
V ” |
Одержання комплексно - сполученого вектора |
M |
M ” |
Одержання комплексно - сполученої матриці;
|
V |
V Ctrl – |
Векторизація вектора V; |
M |
M Ctrl – |
Векторизація матриці M; |
M<n> |
M Ctrl ^n |
Виділення n-го стовпця матриці M; |
Vn |
V [ n |
Виділення n-го елемента вектора V; |
Mm,n |
M [(m,n) |
Виділення елемента (m, n) матриці M. |
Під поняттям "векторизація" мається на увазі одночасне проведення математичних операцій у їхньому скалярному значенні над всіма елементами вектора або матриці, позначеними векторизацією. Це можна розуміти і як можливість паралельних обчислень.
Якщо А и В - вектори, то А*В дає скалярний добуток цих векторів. Але той же добуток під знаком векторизації створює новий вектор, кожен j-й елемент якого є добуток j -х елементів векторів А и В. Векторизація дозволяє використовувати скалярні оператори й функції з масивами.