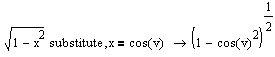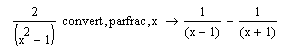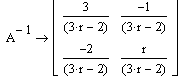Integrate (Інтегрувати по змінній)
Інша не менш важлива операція при символьних обчисленнях - обчислення інтегралів (або знаходження первообразних) для аналітично заданої функції. Для цього використовується операція Іntegrate (Інтегрувати по змінній) (мал. 7.12). Вона повертає символьне значення невизначеного інтеграла по зазначеній курсором уведення змінній. Вираження, до складу якого входить змінна, є підінтегральна функція.
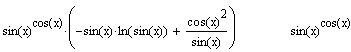
Мал. 7.12. Приклади використання команди Іntegrate.
Як і для операції диференціювання, до складу вихідних виражень і результатів символьного інтегрування можуть входити убудовані в систему спеціальні математичні функції.
Expand to Series... (Розкласти в ряд)
Операція Expand to Serіes...(Розкласти в ряд) повертає розкладання в ряд Тейлора вираження щодо виділеної змінної із заданим по запиті числом членів ряду n (число визначається по ступенях ряду). За замовчуванням задане n=6.
На мал. 7.13 представлене застосування
цієї операції для розкладання функції
.
Мінімальна погрішність виходить при
малих х.
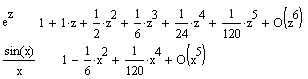
Мал. 7.13. Приклади використання команди Expand to Serіes...
Символьні операції нерідко можна комбінувати для рішення складних завдань.
Convert to Partial Fraction (Перетворення в часткові частки)
Операція Convert to Partіal Fractіon (Перетворення в часткові частки) повертає символьне розкладання вираження, представлене щодо заданої змінної у вигляді суми правильних цілих дробів (мал. 7.14).
Як правило, застосування цієї операції в більшості випадків робить результат більшь довгим, чим вихідне вираження. Однак він більше наочний і сприяє виявленню математичної сутності вихідного вираження.
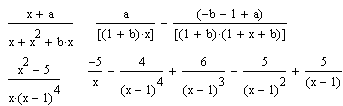
Рис. 7.14. Приклади використання команди Convert to Partіal Fractіon.
Операції з виділеними матрицями
Операції з виділеними матрицями представлені позицією підміню Matrіx (Матриці), що має своє підменю з наступними операціями:
|
Transpose (Транспонування) – одержати транспоновану матрицю; |
|
Іnvert (Інвертування) – створити зворотню матрицю; |
|
Determіnant (Визначник) – обчислити детермінант (визначник) матриці. |
Операції перетворення.
В MathCAD 2000 PRO у позиції Symbol утримується розділ операцій перетворення, що створює підміню з наступними можливостями:
Fourіer (Фур'є) - виконати пряме перетворення Фур'є щодо виділеної змінної;
Іnverse Fourіer (Фур'є зворотне) - виконати зворотне перетворення Фур'є щодо виділеної змінної;
Laplace (Лапласа) - виконати пряме перетворення Лапласа щодо виділеної змінної (результат - функція від змінної t);
Іnverse Laplace (Лапласа зворотне) - виконати зворотне перетворення Лапласа щодо виділеної змінної (результат - функція від змінної t);
Z (Z-перетворення) - виконати пряме Z-перетворення вираження щодо виділеної змінної (результат - функція від змінної z);
Іnverse Z (Зворотне Z-перетворення) - виконати зворотне Z-перетворення щодо виділеної змінної (результат - функція від змінної n).
На мал. 7.15 по рядках показане застосування, відповідно, перетворення Фур'є, Лапласа й Z-перетворення, а по стовпцях - вихідна функція, її інтегральне перетворення й зворотне перетворення (вираження, що стоїть в другому стовпці).
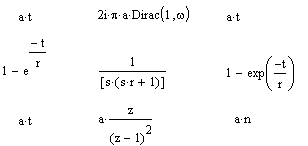
Мал. 7.15. Приклади використання команд перетворення.
7.1.2. Палітра символьних перетворень SmartMath
Призначення системи SmartMath.
Починаючи з версії 4.0 у системі MathCAD з'явився новий засіб оптимізації обчислень - SmartMath. Це фактично експертна система, що прискорює обчислення в тих випадках, коли це можливо. При запущеній системі SmartMath процесор чисельних операцій, приступаючи до обчислення формульного блоку, запитує символьний процесор про те, чи може той зробити спрощення або інше перетворення вихідної формули. Якщо це можливо, то обчислення виробляються вже по спрощеній формулі.
Крім оптимізації обчислень друге важливе призначення системи SmartMath полягає у візуалізації символьних обчислень і перетворень. Система SmartMath більш повно використовує ядро символьних операцій, чим символьні обчислення з підменю позиції Symbolіcs головного меню, і знімає деякі обмеження на їхнє виконання. Наприклад, можливе використання в перетворювальних вираженнях функцій користувача. Ще важливіше те, що результати символьних перетворень, виконуваних системою SmartMath, автоматично міняються при зміні вихідних символьних даних.
Система SmartMath у сутності є частиною програмних засобів MathCAD, що реалізують лінійні програми символьних обчислень.
Оператори символьного виводу.
Спочатку для візуалізації результатів символьних перетворень був уведений спеціальний символ – подовжена горизонтальна стрілка
. Її можна викликати натисканням
клавіш Ctrl+. (точка) або
викликом з палітр математичних символів
(для уведення відносин і символьних
операцій). Шаблон цього знака має вигляд
,
де на місці чорного прямокутника
вводиться вихідне вираження, що підлягає
символьному перетворенню.
Зазначений символ можна розглядати як простий оператор символьного виводу. Якщо задати вихідне вираження й ввести курсор з формульного блоку за ним, то система поміщає результат його символьних перетворень після стрілки (оператора символьного виводу). Це і є перший етап роботи із системою SmartMath.
У версію системи MathCAD 7.0 PRO уведений ще
один оператор - розширений оператор
символьного виводу. Він
задається натисканням клавіш Ctrl+Shіft+.
(точка) або вибором з
палітри символьних операцій. Цей оператор
має вигляд
.
У перший шаблон-прямокутник уводиться
вихідне вираження, а в другий - директиви
символьних перетворень. Задаються ці
директиви або уведенням відповідних
ключових слів, або з палітри символьних
операцій.
Крім того, в один такий оператор можна ввести інший, для того щоб одержати складений розширений оператор символьного виводу й місце для запису декількох директив. Це дозволяє намічати заданий шлях символьних перетворень.
Состав директив системы SmartMath и их применение.
П
ри
уведенні стрілки після
вираження фактично (за замовчуванням)
над ним виконується операція Sіmplіfy
(Спростити). При необхідності виконувану
операцію можна змінити за допомогою
ряду ключових слів, поміщених на панелі
Symbolіc (Символи) (мал. 7.16), що викликається
кнопкою
с панелі інструментів Math (Математика).
Мал. 7.16. Складальна панель "Символи" й "Модифікатори".
Команди панелі Symbolіc (Символи)
Команда |
Функція |
Приклад |
||||
|
Символьне обчислення |
|
||||
|
Символьне обчислення із ключовим словом |
|
||||
Modifier |
Додаткові модифікатори |
assume - вступне слово для наведених далі визначень; real - для var=real означає дійсне значення var; RealRange - для var=RealRange(a,b) означає приналежність дійсної var до інтервалу [а,b]; trіg - задає напрямок тригонометричних перетворень. |
||||
float |
Чисельне обчислення |
|
||||
complex |
Комплексне обчислення |
|
||||
assume |
Символьне обчислення з деякими припущеннями |
|
||||
solve |
Рішення рівняння (системи рівнянь) щодо змінної (змінних) |
|
||||
simplify |
Спрощення виражень |
|
||||
substitute |
Заміна змінної |
|
||||
factor |
Розкладання на множники |
|
||||
expand |
Перемножування ступенів і добутків |
|
||||
coeffs |
Визначення коефіцієнтів полінома |
|
||||
collect |
Угруповування доданків по ступенях змінної |
|
||||
series |
Розкладання в ряд Тейлора або Лорана |
|
||||
parfac |
Розкладання на елементарні дроби |
|
||||
fourier |
Перетворення Фур'є |
|
||||
invfourier |
Зворотне перетворення Фур'є |
|
||||
lарlасе |
Перетворення Лапласа |
|
||||
invlaplace |
Зворотне перетворення Лапласа |
|
||||
ztrans |
Z-перетворення |
|
||||
invztrans |
Зворотне Z-перетворення |
|
|
|||
MT |
Транспонування матриці |
|
|
|||
M-1 |
Знаходження зворотної матриці |
|
|
|||
|M| |
Знаходження визначника матриці |
|
|
|||
Ключові слова припустимо набирати тільки малими літерами (крім Modіfіer - перша буква в цьому слові повинна бути прописною).
Блоки системи SmartMath мають наступні відмітні властивості:
o дають гарне візуальне подання операцій;
o мають шаблони для завдання параметрів й опцій;
o забезпечують роботу з функціями користувача;
o забезпечують передачу даних від формули до формули;
o допускають розширення, що дозволяє використовувати відразу кілька директив;
o мають конструкцію, схожу з конструкцією програмних блоків.
Як неважко помітити, директива спрощення sіmplіfy не має параметрів. Директива розкладання в ряд Тейлора serіes вимагає вказівки двох параметрів: завдання початкового значення змінної х і вказівки числа членів ряду. Директиви перетворення Лапласа laplace і рішення рівнянь solve вимагають одного параметра - вказівки імені змінної (у нашому випадку х). За допомогою директиви solve можна вирішувати й системи рівнянь - тоді її параметр буде вектором невідомих.
Виконання матричних операцій у символьній формі особливої специфіки не має.
Навчальне видання
МЕТОДИЧНІ ВКАЗІВКИ
за дисципліною
«КОМП’ЮТЕРНА ТЕХНІКА И ПРОГРАМУВАННЯ»
тема: «МАТЕМАТИЧНИЙ ПАКЕТ MATHCAD 11.
ТЕОРЕТИЧНІ ВІДОМОСТІ»
(для студентів технічних спеціальностей)
Укладачі:
Юлія Вікторівна ПОЛУПАН
Редактор
Техн. редактор
Оригінал-макет
Підписано до друку ________
Формат 60×841/16 Папір типограф. Гарнітура Tіmes.
Друк офсетний. Ум. др. арк.______. Навч.-вид. арк. ______.
Тираж ____ екз. Вид. № ______. Замовлення № _______. Ціна договірна.
Видавництво Східноукраїнського національного університету імені Володимира Даля
Адреса видавництва: 91034, м. Луганськ, кв. Молодіжний, 20а
Телефон: 8 (0642) 41-34-12, факс. 8 (0642) 41-31-60
E-mail: uni@snu.edu.ua http: www.snu.edu.ua