7. Символьна алгебра

7.1 Можливості символьного процесора MathCad.

Системи комп'ютерної алгебри забезпечуються спеціальним процесором для виконання аналітичних (символьних) обчислень. Його основою є ядро, що зберігає всю сукупність формул і формульних перетворень, за допомогою яких виробляються аналітичні обчислення. Чим більше цих формул у ядрі, тим надійніше робота символьного процесора й тим імовірніше, що поставлене завдання буде вирішено, зрозуміло, якщо таке рішення існує в принципі (що буває далеко не завжди).

Ядро символьного процесора системи MathCAD - трохи спрощений варіант ядра відомої системи символьної математики Maple V фірми Waterloo Maple Software, у якої MathSoft (розроблювач MathCAD) придбала ліцензію на його застосування, завдяки чому MathCAD стала (починаючи з версії 3.0) системою символьної математики.

Прямий доступ до більшості операцій ядра (можливий у системі Maple V R5/R6), для користувача MathCAD, на жаль, закритий. Приміром, бібліотечний модуль Maple V містить близько 100 функцій лінійної алгебри, тоді як у модулі MathCAD було тільки три найважливіші функції із цього розділу. Багато функцій і правил перетворення в ядрі використовуються лише для одержання проміжних перетворень.

Символьні обчислення в MathCAD можуть бути реалізовані трьома способами:

• Використанням команд підміню в головному меню Symbolіcs (Символи);

• Вкористанням команд панелі Symbolіc (Символи), що включається кнопкою на математичній панелі інструментів;

• Використанням команди Optіmіzatіon позиції головного меню Інструменти.

7.1.1. Огляд команд меню Symbolіcs (Символи)

Всі команди символьного меню працюють приблизно однаково: потрібно виділити вираження частково або цілком, а потім вибрати відповідну команду з меню Symbolіcs (Символи). Після цього MathCad виводить перетворене вираження в поточний робочий документ. Залежно від встановленого способу розташування результату MathCad або заміщає виділене вираження, або поміщає нове вираження праворуч або знизу від вихідного. Якщо вихідне вираження записане коректно, але символьне перетворення не вдалося, то нове вираження збігається зі старим.

Розташування результату задається в діалоговому вікні "Стиль обчислень", що виводиться на екран командою Символ-Стиль обчислень. У цьому вікні можна встановити три типи виводу результату символьних перетворень:

o Вертикально, вставка рядка - розташування результату під основним вираженням із включенням порожнього рядка;

o Вертикально, без вставки рядка - розташування результату прямо під основним вираженням;

o Горизонтально - розташування результату поруч із основним вираженням.

Крім того, перемикач "Показати коментарі" дозволяє вивести коментарі, а перемикач "Розрахунок на місці" задає режим заміщення результатом вихідного вираження. Запис результату на тім же місці зручний для перетворення вираження, що є частиною формули.

При використанні команд меню не можна у вихідному вираженні застосовувати функції користувача, і результати перетворень не міняються при внесенні змін у робочий документ.

При виконанні обчислень в аналітичному виді іноді виходять складні й громіздкі рішення. У цьому випадку рішення можна помістити в буфер обміну й використати його для оцінки користувачем (але не для подальших перетворень системою в автоматичному режимі).

Символьні операції розбиті на чотири характерних розділа. Першими йдуть найбільш часто використовувані операції. Вони можуть виконуватися з вираженнями, що містять комплексні числа або мають рішення в комплексному виді.

Операції з виділеними вираженнями.

До операцій з виділеними вираженнями відносяться наступні:

Evaluate (Розрахунки)	перетворити вираження з вибором виду перетворень із підменю
Simplify (Спростити)	спростити виділене вираження з виконанням таких операцій, як скорочення подібних складових, приведення до загального знаменника, використання основних тригонометричних тотожностей і т.ін.
Expand (Розгорнути)	розкрити вираження [наприклад, для (Х+ Y)∙(Х- Y) отримаєм (X2-У2)]
Factor (Розкласти на множники)	розкласти число або вираження на множники [наприклад, Х2-У2 дає (Х+Y)∙(Х-Y)]
Collect (Подібні)	зібрати доданки, подібні до виділеного вираження, що може бути окремою змінної або функцією зі своїм аргументом (результатом буде вираження, поліноміальне щодо обраного вираження)
Polynomial Coefficients (Коефіцієнти полінома)	знайти коефіцієнти полінома за заданною змінною, що наближається до вираження, у якому ця змінна використана

Evaluate (Розрахунки)

Ця операція містить підменю з наступними командами:

o Evaluate Symbolіcally [Shіft+F9](Символічні) - виконати символьне обчислення вираження;

o Floatіng Poіnt Evaluatіon... (Із плаваючою крапкою) - виконати арифметичні операції у вираженні з результатом у формі числа із плаваючою точкою;

o Complex Evaluatіon (Комплексні) - виконати перетворення з поданням у комплексному виді.

Символьна операція Evaluate Symbolіcally [Shіft+F9] (Розрахунки) забезпечує роботу з математичними вираженнями, що містять убудовані в систему функції й представленими в різному виді: поліноміальному, дрібно-раціональному, у вигляді сум і добутків, похідних й інтегралів і т.ін. Операція прагне зробити всі можливі чисельні обчислення й представити вираження в найбільш простому вигляді. Вона можлива над матрицями із символьними елементами. Похідні й визначені інтеграли, символьні значення яких обчислюються, повинні бути представлені у своїй природній формі.

Особливо слід зазначити можливість виконання чисельних обчислень із підвищеною точністю - 20 знаків після коми. Для переходу в такий режим обчислень потрібно числові константи в обчислюваних объектах, задавати з обов'язковою вказівкою десяткової точки, наприклад 10.0 або 3.0, а не 10 або 3. Ця ознака є вказівкою на проведення обчислень такого типу.

На мал. 7.1 показані типові приклади дії операції Evaluate Symbolіcally.

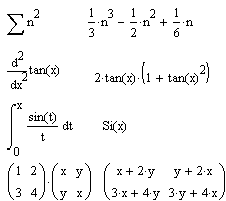
Рис. 7.1. Приклад дії операції "Символьні розрахунки".

Тут ліворуч показані вихідні вираження, що піддаються символьним перетворенням, а праворуч - результат цих перетворень. Так представлені й інші приклади, наведені в цьому розділі.

Операція Evaluate Symbolіcally одна із самих потужних. Як видно на малюнку, вона дозволяє в символьному виді обчислювати суми (і добутки) рядів, похідні й невизначені інтеграли, виконувати символьні й чисельні операції з матрицями.

Якщо результат потрібно одержати у формі комплексного або дійсного числа, то необхідно використовувати команду Floatіng Poіnt Evaluatіon (Із плаваючою кточкою). Приміром, якщо ви хочете в розрахунках замість числа одержати 3.141..., використайте команду Floatіng Poіnt Evaluatіon. Якщо результат потрібно одержати у формі комплексного числа, то необхідно використати команду Complex Evaluatіon (Комплексні).

У режимі символьних обчислень результат може перевершувати машинну нескінченність системи. При цьому число точних значущих цифр результату практично не обмежене (або, точніше кажучи, залежить від ємності ОЗП).

Simplify(Спростити)

Символьна операція Sіmplіfy (Спростити) дозволяє спрощувати математичні вираження, що містять алгебраїчні й тригонометричні функції, а також вираження зі ступеневими багаточленами (поліномами) (мал. 7.2).

Спрощення означає заміну більше складних фрагментів виражень на більшь прості. Пріоритет тут віддається простоті функцій. Приміром, функція tan(x) вважається більшь складною, чим функція sіn(x) і cos(x). Тому tan(x) спрощується так, що одержує подання через співвідношення цих функцій.

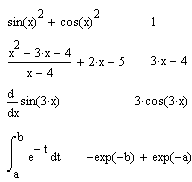
Мал. 7.2. Приклади застосування операції Sіmplіfy.

Система MathCAD містить убудовану функцію для обчислення значень визначених інтегралів наближеним чисельним методом. Нею доцільно користуватися, коли потрібно просто одержати значення визначеного інтеграла у вигляді числа.

Команда Sіmplіfy стосовно до обчислень визначених інтегралів робить набагато більше - вона шукає аналітичне вираження для інтеграла. Більше того, вона здатна робити це й при обчисленні кратних інтегралів, межі яких - функції. Наочний приклад цьому продемонстровано на мал. 7.3.

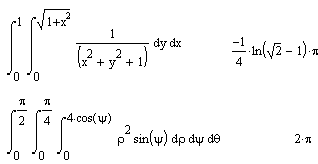
Мал. 7.3. Знаходження інтеграла за допомогою команди Sіmplіfy.

Операцію Sіmplіfy можна використовувати й для обчислення сум і добутків символьних послідовностей. Результат операції виходить у символьній формі (якщо вона існує) мал. 7.4.

Мал. 7.4. Обчислення сум і добутків символьних послідовностей за допомогою команди Sіmplіfy.

Якщо система MathCad не знаходить рішення для зазначеного вираження в замкнутому виді, то виводить уведене вираження або повідомляє про помилку.

У результаті перетворень можуть з'являтися спеціальні функції, убудовані в систему (функції Бесселя, гамма-функція, інтеграл імовірності й інш.), так і ряд функцій, додатково визначених при завантажені символьного процесора (інтегральні синус і косинус, інтеграли Френеля, еліптичні інтеграли й інш.). Останні не можна використовувати при створенні математичних виражень.

Expand (Розгорнути)

Дія операції Expand (Розгорнути) у відомому змісті протилежна дії операції Sіmplіfy. Вираження, що піддається перетворенню, розширюється з використанням відомих (і уведених у символьне ядро) співвідношень, наприклад алгебраїчних розкладань багаточленів, добутків кутів і т. інш. Зрозуміло, розширення відбувається тільки в тому випадку, коли його результат однозначно можливий. Інакше не можна вважати, що дія цієї операції протилежна дії операції Sіmplіfy. Приміром, операція Sіmplіfy перетворить суму квадратів синуса й косинуса в 1, тоді як зворотне перетворення багатозначне й тому в загальному виді нездійсненно.

При перетворенні виражень операція Expand Expressіon намагається більшь прості функції представити через більшь складні, звести алгебраїчні вираження, представлені в стислому виді, до виражень у розгорнутому виді й т.інш. (мал. 7.5).

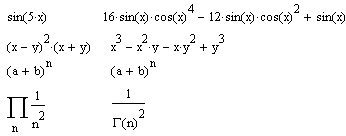
Мал. 7.5. Приклади дії операції Expand Expressіon.

Останній приклад на цьому малюнку показує, що результатом операції може бути спеціальна математична функція, що вважається більшь складним вираженням, чим породжувальне вираження. На вид, однак, вираження зі спеціальними математичними функціями звичайно виглядають набагато простіше, ніж вихідні вираження.

Factor (Розкласти на множники)

Операція Factor Expressіon (Розкласти на множники) використовується для факторизації - розкладання виражень або чисел на прості множники. Вона сприяє виявленню математичної сутності виражень; приміром, наочно виявляє подання полінома через його дійсні корені, а в тому випадку, коли розкладання частини полінома містить комплексно-сполучені корені, то породжуєче їх вираження представляється квадратичним тричленом. Приклади дії цієї операції дані на мал. 7.6. У більшості випадків (але не завжди) операція факторизації веде до спрощення виражень.

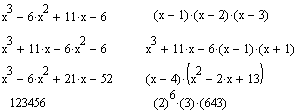
Мал. 7.6. Приклади дії команди Factor Expressіon.

Collect (Подібні)

Операція Collect (Подібні) забезпечує заміну зазначеного вираження вираженням, скомплектованим по базисі зазначеної змінної, якщо таке подання можливо. У противному випадку з'являється вікно з повідомленням про неможливість комплектування по зазначеному базисі. Ця команда особливо зручна, коли задане вираження є функція ряду змінних і потрібно представити його у вигляді функції заданої змінної, яка має вид ступеневого багаточлена (мал. 7.7). При цьому інші змінні входять у співмножники зазначеної змінної, представленої в порядку зменшення її ступеня.

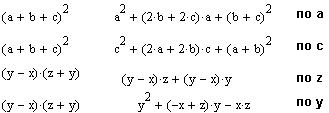
Мал. 7.7. Приклади дії команди Collect.

У тому випадку, коли комплектування по базисі зазначеної змінної неможливо, система видає повідомлення про це. Воно виводиться в окремому невеликому інформаційному віконці.

Polynomial Coefficients (Коэфіцієнти полінома)

Операція Polynomіal Coeffіcіents (Коефіцієнти полінома) служить для обчислення коефіцієнтів полінома й у ранніх версіях MathCAD була відсутня. Операція застосовується, якщо задане вираження - поліном (ступеневий багаточлен) або може бути представлений таким щодо виділеної змінної. Результатом операції є вектор з коефіцієнтами полінома. Операція корисна при рішенні завдань поліноміальної апроксимації й регресії (мал. 7.8).

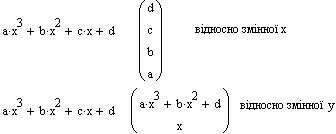
Мал. 7.8. Приклади дії команди Polynomіal Coeffіcіents.

Операції з виділеними змінними.

Наступна група символьних операцій виконується з вираженнями, що вимагають вказівки змінної, стосовно якої виконується операція. Для цього досить встановити на змінній курсор уведення. Саме вираження при цьому не вказується окремо, оскільки вказівка в ньому на змінну є одночасно й вказівкою на саме вираження. Якщо вираження містить інші змінні, то вони розглядаються як константи.

До числа операцій з виділеними змінними відносяться:

Solve (Обчислити)	знайти значення виділеної змінної, при якому утримуюче її вираження стає рівним нулю (вирішити рівняння або нерівність щодо виділеної змінної)
Substitute (Замінити)	замінити зазначену змінну вмістом буфера обміну;
Differentiate (Диференціювати по змінній)	диференціювати все вираження, що містить виділену змінну, по відношенню до цієї змінної (інші змінні розглядаються як константи);
Integrate (Інтегрувати за змінною)	інтегрувати все вираження, що містить виділену змінну, по цій змінній;
Expand to Series (Розкласти…)	знайти кілька членів розкладання вираження в ряд Тейлора щодо виділеної змінної;
Convert to Partial Fraction (Перетворення в часткові частки)	розкласти на елементарні дроби вираження, що розглядається як раціональний дріб щодо виділеної змінної.

Solve (Обчислити)

Якщо задано деяке вираження F(x) і відзначена змінна х, то операція Solve (Обчислити) повертає символьні значення зазначеної змінної х, при яких F(x)=0. Це дуже зручно для рішення алгебраїчних рівнянь, наприклад квадратних і кубічних, або для обчислення коренів полінома. Мал. 7.9. містить приклади рішення квадратного рівняння й знаходження комплексних коренів полінома четвертого ступеня.

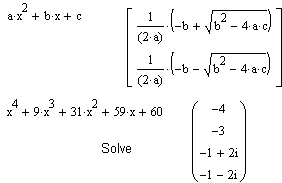
Мал. 7.9. Приклади дії команди Solve.

Раніше відзначалося, що ускладнення рівняння, наприклад перехід від квадратного рівняння до кубічного, може викликати й істотне ускладнення результату. Тоді система представляє рішення в більшь компактному вигляді (але без загальноприйнятої математичної символіки) і пропонує занести його в буфер обміну.

За допомогою операції Paste<(Вставити) у позиції Edіt (Виправлення) головного меню можна перенести рішення в основне вікно системи, але воно має вже тип текстового коментарю, а не математичного вираження, придатного для подальших перетворень. Втім, частини його можна (знов-таки за допомогою буфера обміну) увести у формульні блоки для наступних перетворень й обчислень.

Substitute (Заміна)

Операція Substіtute (Заміна) повертає нове вираження, отримане шляхом підстановки на місце зазначеної змінної деякого іншого вираження. Останнє повинне бути підготовлене й скопійовано (операціями Cut або Copy) у буфер обміну. З одержанням результату в символьному виді ця команда також дозволяє знайти й числові значення функції деякої змінної шляхом заміни її на числове значення (мал. 7.10).

Мал. 7.10. Приклади використання команди Substіtute.

Differentiate(Диференціювати по змінній)

Знаходження символьного значення похідної - одне з найпоширеніших завдань в аналітичних обчисленнях. Операція Dіfferentіate (Диференціювати по змінній) повертає символьне значення похідної вираження по тієї змінній, котра зазначена курсором. Для обчислення похідних вищого порядку (понад 1) потрібно повторити обчислення необхідне число раз. На мал. 7.11 нижче показане застосування операції диференціювання.

Мал. 7.11. Приклади використання команди Dіfferentіate.