6.2.Системи рівнянь.

Розглянемо рішення системи N нелінійних рівнянь із m невідомими. Рівнянь може бути як більше, так і менше числа змінних. Для рішення систем є спеціальний обчислювальний блок, що складається із чотирьох частин, що йдуть послідовно один за одним:

- задаються початкові наближення по всім змінним системи;

- записується ключове слово Gіven;

- записується система з логічними операторами у вигляді рівностей й, можливо, нерівностей;

- записується убудована функція для рішення системи щодо змінних .

Вставляти логічні оператори рівностей або нерівностей треба, користуючись панеллю інструментів Boolean (Бульові оператори). При уведенні із клавіатури, логічний знак рівності вводиться сполученням клавіш <Ctrl>+<=>. Блок Gіven/Fіnd використовує для пошуку рішення ітераційні методи, тому, як і для функції root, потрібно задавати початкові значення для всіх . Зробити це необхідно до ключового слова Gіven. Значення функції Fіnd є вектор, складений з рішення по кожній змінній. Таким чином, число елементів вектора дорівнює числу аргументів Fіnd. На мал. 6.5 наведений приклад рішення системи двох рівнянь.

У першому рядку на мал. 6.5 змінним х и y, щодо яких буде вирішуватися система привласнюються початкові значення. Потім слідує ключове слово Gіven і вводяться функції із двома логічними операторами, що виражають систему рівнянь, яка розглядається. Завершує обчислювальний блок функція Fіnd, значення якої привласнюється вектору v. Наступний рядок показує зміст вектора с, тобто рішення системи. Перший елемент вектора є перший аргумент функції Fіnd, другий елемент - її другий аргумент.

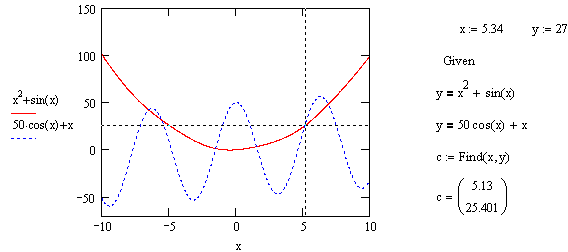
Мал. 6.5. Рішення системи рівнянь.

Графічна інтерпретація розглянутої системи представлена на графіку мал. 6.5 Кожне з рівнянь показано на площині XY графіком. Перше - суцільною кривою, друге - пунктиром. Дві точки перетинання кривих відповідають одночасному виконанню обох рівнянь, тобто шуканим дійсним корінням системи. На малюнку знайдено тільки одне із шести рішень. Щоб відшукати інші рішення, варто повторити обчислення, змінивши початкові значення так, щоб вони лежали ближче до іншої точки перетинання графіків, наприклад .

Число рівнянь із числом невідомих у розв'язуваних системах може й не збігатися. Більше того, в обчислювальний блок можна додати додаткові умови у вигляді нерівностей. Наприклад, введення обмеження на пошук тільки негативних значень х або y.

Якщо спробувати вирішити несумісну систему, MathCAD видасть повідомлення про помилку, що говорить, що жодного рішення не знайдено, і пропозицію спробувати поміняти початкові значення або значення погрішності.

Особливу обережність варто дотримувати при рішенні систем із числом невідомих більшим, ніж число рівнянь. Наприклад, можна видалити одне із двох рівнянь із розглянутого приклада (мал. 6.5), спробувавши вирішити єдине рівняння с двома невідомими х и у. У такій постановці завдання має нескінченну безліч коренів. Однак навіть якщо коренів нескінченно багато, чисельний метод буде робити розрахунки тільки доти, поки логічні вираження в обчислювальному блоці не будуть виконані (у межах погрішності). Після цього ітерації будуть зупинені й видане рішення. У результаті буде знайдена всього одна пара значень (х,у), виявлена першою.

Обчислювальним блоком з функцією Fіnd можна знайти й корінь рівняння з одним невідомим. Дія Fіnd у цьому випадку зовсім аналогічно вже розглянутим у даному розділі прикладам. Завдання пошуку кореня розглядається як рішення системи, що складається з одного рівняння. Єдиною відмінністю буде скалярний, а не векторний тип числа, що повертається функцією Fіnd.